SP5830 ALTPERM - Alternating Permutations 题解

SP5830 ALTPERM - Alternating Permutations 题解

考虑 \(n\) 在整个排列中的位置，显然他只有可能出现在 \(A_i, 2|i\)，而且确定了它的位置之后，剩下的左右两部分独立（对于 \(1\) 类似），所以我们根据这个递归的结构设计 DP。

如果状态设计是 \(f_{l, r}\) 就太多了，每次我们只会在最值点转移，所以可以把状态变成 \(f_{i, j}\) 表示只考虑 \((A_i, j]\) 或 \([j, A_i)\) 这个区间的答案，这样一来状态总数是 \(O(nk)\) 的，转移枚举最大值/最小值点即可，如果 \(A_i\) 是最大值那么转移最小值点，否则转移最大值点，这样保证了区间端点至少有一个是关键点。

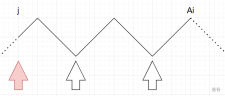
比较坑的一点是 \(j\) 也有可能成为极值点，即使它不在 \(A\) 里面，如图（箭头所指的地方是转移点）：

#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>
#define int long long
using namespace std;
const int N = 2e4 + 10, K = 25, mod = 1e9 + 7;
int n, k, a[N], f[K][N], fac[N], ifac[N], ne[N], pr[N];
int qmi(int a, int b) {
    int res = 1;
    while(b) {
        if(b & 1) res = res * a % mod;
        a = a * a % mod, b >>= 1; 
    }
    return res;
}
void init() {
    fac[0] = ifac[0] = 1;
    for(int i = 1; i < N; i ++) fac[i] = fac[i - 1] * i % mod;
    ifac[N - 1] = qmi(fac[N - 1], mod - 2);
    for(int i = N - 2; i; i --) ifac[i] = ifac[i + 1] * (i + 1) % mod;
}
int C(int n, int m) {
    if(n < m || n < 0 || m < 0) return 0;
    return fac[n] * ifac[m] % mod * ifac[n - m] % mod;
}
int DP(int i, int j) {
    if(f[i][j]) return f[i][j];
    int ans = 0, len = abs(a[i] - j);
    if(j < a[i]) {
        if(j >= a[i - 1]) return f[i][j] = 1;
        if((i & 1) == (ne[j] & 1)) ans += DP(i, j + 1);
        for(int p = i - 1; p >= 1 && a[p] > j; p -= 2) {
            ans = (ans + C(len - 1, a[p] - j) * DP(p, j) % mod * DP(p, a[i] - 1)) % mod;
        }
    }
    else {
        if(j <= a[i + 1]) return f[i][j] = 1;
        if((i & 1) == (pr[j] & 1)) ans += DP(i, j - 1);
        for(int p = i + 1; p <= k && a[p] < j; p += 2) {
            ans = (ans + C(len - 1, j - a[p]) * DP(p, j) % mod * DP(p, a[i] + 1)) % mod;
        }
    }
    return f[i][j] = ans;
}
void work() {
    cin >> n >> k;
    for(int i = 1; i <= k; i ++) cin >> a[i];
    for(int i = 1; i < k; i ++) {
        for(int j = a[i] + 1; j <= a[i + 1]; j ++) pr[j] = i;
         for(int j = a[i]; j < a[i + 1]; j ++) ne[j] = i + 1;
    }
    ne[n] = k + 1, pr[1] = 0;
    a[k + 1] = n + 1;
    memset(f, 0, sizeof f);
    int ans = 0;
    for(int i = 2; i <= k; i += 2) {
        ans = (ans + C(n - 1, a[i] - 1) * DP(i, 1) % mod * DP(i, n)) % mod; 
    }
    cout << ans << '\n';
}
signed main() {
    ios::sync_with_stdio(0), cin.tie(0);
    int T; cin >> T, init();
    while(T --) work();
    return 0;
}