关于竞赛图的一些性质

关于竞赛图的一些性质

比分序列

一个竞赛图的比分序列 \(c\) 定义为：按出度从小到大排序形成的序列，可以直观理解成在一场单循环比赛里最弱到最强的人的排名。

本文假设 \(d_i\) 为 \(i\) 号点的出度。

Lemma 1

对竞赛图缩点之后形成的 DAG 形如一条链。

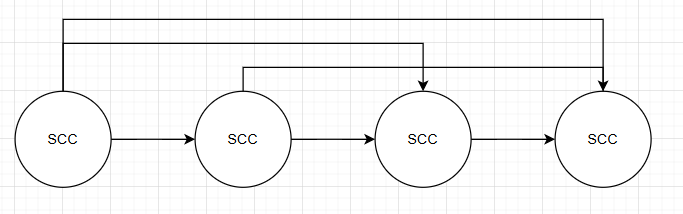
考虑归纳，新加入一个点之后，如果这个点和某一个 SCC 同时拥有出边和入边，那么它就属于这个 SCC，否则可以推出一个点和某一个 SCC 之间的边一定是同向的，那么此时这个点在这条链上一定存在一个分界线，使得前半部分是入边后半部分是出边，这样一来，直接把这个点放到这个分界线上就行了。

Lemma 2（兰道定理）

一个图是竞赛图 当且仅当 对于比分序列的每个前缀 \(i\) 都满足 \(\sum_{k = 1}^id_{c_k} \ge \binom{i}{2}\)，且在 \(i = n\) 时取等。

Lemma 3

一个 \(n(n\ge 4)\) 阶强连通竞赛图一定存在一个 \(n - 1\) 阶子强连通竞赛图。

考虑归纳，对于任意一个 \(n - 1\) 阶竞赛图 \(G\)，如果其添加一个点 \(z\) 之后变成了一个强连通竞赛图，那么：

如果对 \(G\) 进行强连通分量的缩点之后，按拓扑序排好，形成的 SCC 为 \(v_1, v_2, ..., v_m\)。

1. \(m = 1\) 显然。
2. \(m \ge 2\)，此时因为新图是强连通图，所以存在 \(x\in v_1, y\in v_m\) \((y,z),(z,x)\in \text E\)，因为 \(n\ge 4\)，所以删除其它任意一个点就行：这样显然不会影响其所在 SCC 内部的强连通性，并且也不会影响整体的强连通性，因为 \(x, y, z\) 没有被删除。

这个引理的推论是对于任意一个 \(n\ge 4\) 阶强连通竞赛图，存在一个点使得将连向的其所有边方向翻转，使得新图还是一个强连通图。

Lemma 4（CF1268D）

一个 \(n(n\ge 7)\) 阶竞赛图最多翻转一个点使得其变成强连通。

考虑归纳，对于任意一个 \(n\) 阶竞赛图 \(G\) 那么：

如果对 \(G\) 进行强连通分量的缩点之后，按拓扑序排好，形成的 SCC 为 \(v_1, v_2, ..., v_m\)。

1. \(m = 1\) 由 Lemma 4 的推论得证。
2. \(m = 2\)，因为 \(n\ge 7\) 由抽屉原理可知，\(v_1, v_2\) 之中必定存在一个 SCC 大小 \(\ge 4\)，所以存在一个点翻转之后其所在 SCC 还是强连通，而由 Lemma 1，其一定存在一条从另一个 SCC 连过来的边，因此翻转之后 \(G'\) 会变成强连通。
3. \(m \ge 3\)，翻转 \(v_i(i\in(1, m))\) 之中任意一个 SCC 就行，和 \(m = 2\) 同样的道理。

Lemma 6

逆比分序列 上的 SCC 形如一个个区间（比分序列上同理）。

反证，如果不是区间，那么一定被分为了多个部分，考虑其中两个部分：

可以明显看到，“孤立点”可以到达SCC内任意一个点，假设不成立，原命题得证。

Lemma 7

比分序列上的 Lemma 6区间 的右端点 \(r\) 当且仅当 \(\sum_{i = 1}^rd_{c_i} = \binom{r}{2}\)。

这个前缀的导出子图一定是一个竞赛图，所以前缀内部连边数就是 \(\binom{r}{2}\)，因此前缀中的点不会向后连边。

由这个引理可以得到一个求出竞赛图强连通分量的算法。

Lemma 8

竞赛图存在一条 哈密顿路径。

考虑归纳，\(n = 1\) 显然，考虑由 \(n - 1\) 阶竞赛图构造出 \(n\) 阶竞赛图的哈密顿路径：

如果点 \(n\) 和 \(1\sim n - 1\) 中所有点的连边都是出边/入边的，那么它可以放到哈密顿路径的开头/结尾。

否则哈密顿路径 \(p\) 中存在 \(i\)，\(p_i\rightarrow n, n\rightarrow p_{i + 1}\)，那么将 \(n\) 插入其中就可以。

Lemma 9

强连通 \(n(n\ge 3)\) 阶竞赛图存在一条 哈密顿回路。

考虑归纳，\(n = 3\) 显然，考虑由 \(n - 1\) 阶竞赛图构造出 \(n\) 阶竞赛图的哈密顿回路：

如果点 \(n\) 和 \(1\sim n - 1\) 中所有点的连边都是出边/入边的，那么此图不强连通。

否则哈密顿路径 \(p\) 中存在 \(i\)，\(p_i\rightarrow n, n\rightarrow p_{i + 1}\)，那么将 \(n\) 插入其中就可以。

例题

P12768 [POI 2018 R3] 三人编程锦标赛 Triinformathlon

官解：用线段树维护二维偏序，区间最大值来优化 kosaraju。

另解：三维偏序算出比分序列，然后根据竞赛图的性质计算 SCC（SCC是连续区间，且 DAG 是链，如果满足朗道定理就是一个 SCC）。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define int long long
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 10;

int n, q, tr[N], deg[N], ans[N], tid[N];
struct qwq {
    int a, b, c, id;
} p[N];
void update(int u, int c) {
    for(; u <= n; u += u & -u)
        tr[u] += c;
}
int query(int u) {
    int sum = 0;
    for(; u > 0; u &= u - 1)
        sum += tr[u]; return sum;
}
void CDQ(int l, int r) {
    int mid = l + r >> 1;
    if(l == r) return ;
    CDQ(l, mid), CDQ(mid + 1, r);
    sort(p + l, p + mid + 1, [](qwq a, qwq b) {return a.b > b.b;});
    sort(p + mid + 1, p + r + 1, [](qwq a, qwq b) {return a.b > b.b;}); 
    for(int i = l, j = mid + 1; i <= mid; i ++) {
        while(j <= r && p[j].b > p[i].b) update(p[j ++].c, 1);
        ans[p[i].id] += query(n) - query(p[i].c);
    }
    for(int i = l, j = mid + 1; i <= mid; i ++)
        while(j <= r && p[j].b > p[i].b) update(p[j ++].c, -1);
} 
int scc[N], idx;

signed main() {
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> p[i].a;
    for(int i = 1; i <= n; i ++) cin >> p[i].b;
    for(int i = 1; i <= n; i ++) cin >> p[i].c, p[i].id = i;
    sort(p + 1, p + n + 1, [](qwq a, qwq b){return a.a > b.a;});
    for(int i = 1; i <= n; i ++) deg[p[i].id] += i - 1 - query(p[i].b), update(p[i].b, 1);
    for(int i = 1; i <= n; i ++) tr[i] = 0;
    for(int i = 1; i <= n; i ++) deg[p[i].id] += i - 1 - query(p[i].c), update(p[i].c, 1);
    for(int i = 1; i <= n; i ++) tr[i] = 0;
    sort(p + 1, p + n + 1, [](qwq a, qwq b){return a.b > b.b;});
    for(int i = 1; i <= n; i ++) deg[p[i].id] += i - 1 - query(p[i].c), update(p[i].c, 1);
    sort(p + 1, p + n + 1, [](qwq a, qwq b){return a.a < b.a;});
    for(int i = 1; i <= n; i ++) tr[i] = 0;
    CDQ(1, n);
    for(int i = 1; i <= n; i ++) deg[i] -= 2 * ans[i], tid[i] = i;
    sort(tid + 1, tid + n + 1, [](int a, int b) {return deg[a] > deg[b];});
    for(int i = 1, j = 1; i <= n; i ++) {
        j = i;
        int sum = deg[tid[j]];
        while(j <= n && sum != (j - i + 1) * (j - i) / 2 + (j - i + 1) * (n - j)) {
            sum += deg[tid[j + 1]];
            j ++;
        }
        idx ++;
        for(int k = i; k <= j; k ++) scc[tid[k]] = idx;
        i = j;
    }
    cin >> q;
    for(int i = 1; i <= q; i ++) {
        int a, b;
        cin >> a >> b;
        cout << (scc[a] <= scc[b] ? "TAK" : "NIE") << '\n';
    }

    return 0;
}