数据结构（一）--- 跳跃表

1、简述

跳跃表（skiplist）是一种优秀的数据查找结构，查找原理类似于2分查找，平均的查找时间复杂度为O(logN)；

其底层基于链表实现，但区别在于含有多层，每个节点的每层都有指向表尾方向最近一个节点的指针；

各种语言对跳跃表的实现可能不同，但主要原理是相同的，所以这里只是所以下原理，

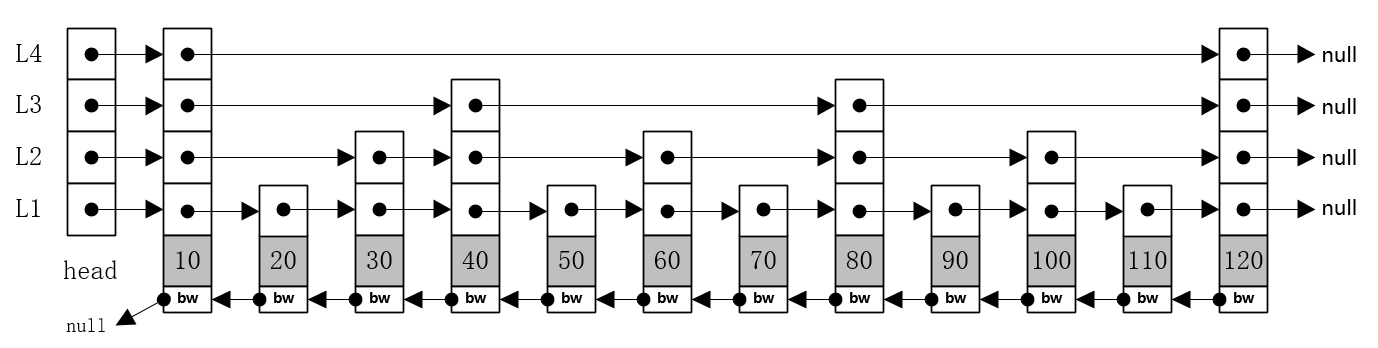
• • 图中是含有四层结构的跳跃表，bw是指向前一个节点的指针，每个节点只有一个，删除时方便。
  • 每个节点都含有一个或多个指向表尾最近一个节点的指针。
  • 最底层（L1层）包含所有的节点。
  • 图中bw笔者参考了Redis实现的跳跃表结构，自主添加上的，便于更好的理解。

 

2、查询

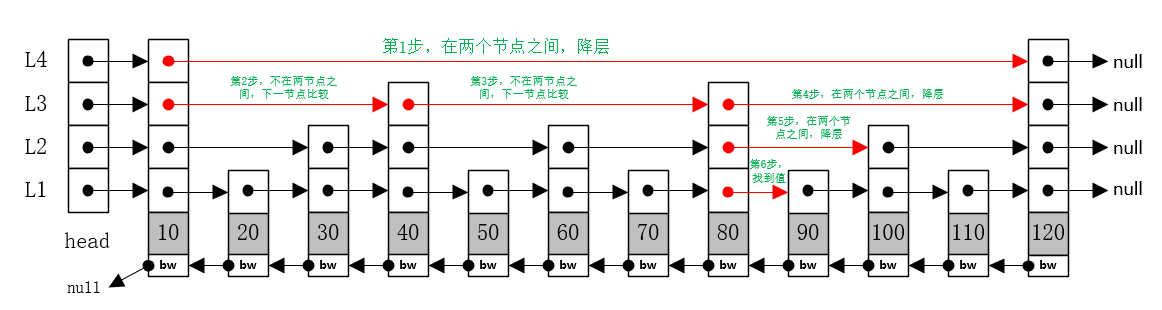
 跳跃表的优秀表现在于查询功能，以上图中查找值为90的节点为例，如果在链表中继续要进行顺序查找，需要进行9步才能查询到，而在上图的跳跃表中则需要6步就能完成，具体步骤如下：

（1）由最高层L4层开始查询，L4层当前节点值10，小于90，则取当前点的下一个节点120，大于90，这时降层到L3层查找；即查找值处于当前节点的值和当前节点下一节点的值之间时，降层查询。

（2）当前节点为10，L3层，取其下一节点40比较，小于90，进行下一步。

（3）节点40，取其下一节点80比较，小于90，进行下一步。

（4）节点80，取其下一节点120比较，大于90，此时将80设置为当前节点，并在当前节点上降层，进行下一步。

（5）当前节点80，L2层，取下一节点100比较，大于90，当前节点不变，直接降层，进行下一步。

（6）当前节点80，L1层，取下一节点90比较，等于90，结束，返回。

一共经过6步，虽然说只节省了3步，但这是在我们查询的是90节点，如果我们查找的是120节点，那么只需要1步便可以查询到了，所以其平均时间复杂度为O(logN)；跳跃表在节点数量少的情况下，性能的提升不明显，当节点在1w以上时，性能提升将会非常明显。

 

3、插入

跳跃表节点的插入过程就是上图中跳跃表结构的构造过程，下面将实现一个只有头结点（不含值）的跳跃表插入节点的过程。

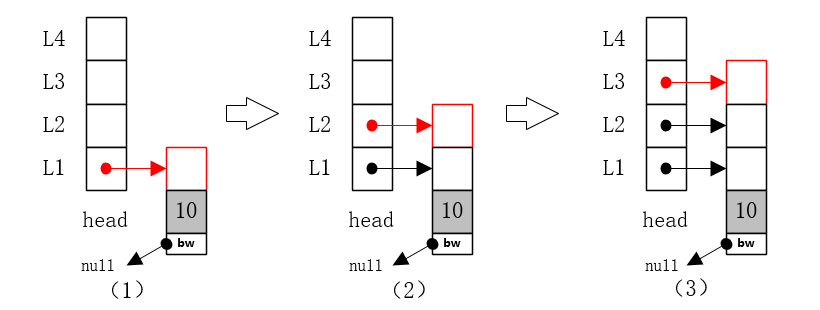
1、插入节点10

（1）节点10插入空跳跃表，插入L1层，如图.

（2）此时抛硬币决定，是否加层；抛硬币正面，节点10增加L2层。

（3）抛硬币决定，是否继续加层，抛硬币正面，节点10继续增加L3层。

（4）继续抛硬币决定，是否继续加层，抛硬币反面，结束加层，节点10插入完成；最终结构如下图（3）。

 

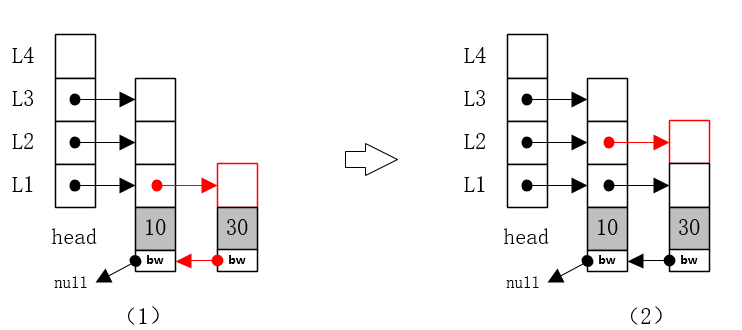
2、插入节点30

 　　（1）节点30插入跳跃表L1层，L1层存在节点10，与其比较，大于10，放入节点10后边，更新节点10L1层指针，指向新节点30，节点30的bw指针，指向节点10，如下图（1）。

（2）此时抛硬币，正面，节点30增加L2层，并更改节点10的L2层的指针，指向新节点30的L2层。

（3）再次抛硬币，反面，结束加层，节点30插入完成；最终结构如下图（2）。 

 

 

以此类推，添加节点过程就是判定层次是否增加的过程；但有几点需要说明一下：

• • 图中所有空层的指针都指向的是NULL ，为使图简洁这点忽略。
  • 头结点的层数，每种实现的语言不一样，初始化的层数不一样，Redis的实现为32层，也就是最高就是32层，不可能再多，其他语言根据设置不同，层数不同；初始化的头结点层指针都指向null。
  • 关于新节点插入哪层的问题，在网上普遍有两种方法，笔者采用的是抛硬币法；两种方法思路如下：
    1. 每层抛硬币法：新节点都插入最底层L1，然后采用抛硬币的方法决定是否在存在上一层；正面存在，进行增加层；反面不存在，则插入结束。
    2. 随机值决定层数：新节点插入之前，先用随机值决定一共有几层，然后根据跳跃表高层含有的节点其低层一定含有的特点，插入数据；随机算法思路是先给定一个概率p，产生一个0到1之间的随机数，如果随机数小于p，则将层加1，直到产生的随机数大于概率p则结束，根据给出的结论，当概率为1/2或者是1/4的时候，整体的性能会比较好（其实当p为1/2的时候，也就是抛硬币的方法）。

4、删除

 节点的删除其实就是一个查找节点，然后修改指针，删除节点的过程；如我们需要删除图中的节点60，步骤如下：

（1）查找节点60，一共需要4步（参考第2节查询）。

（2）修改L2层的前一节点的指针指向后一节点，修改后一节点的bw指针指向前一节点；修改L1层的前一节点指针执行后一节点。

（3）删除节点60，结束。

 

5、总结

• • 在数据规模比较小时，跳跃表形成后可能不是理想的跳跃表结构，但是当数据量增大，结构越接近理想的跳跃表结构。
  • bw指针不是所有的语言的实现都存在，这个是参考了Redis的跳跃表实现，笔者自己加上去的。
  • 跳跃表不同于树结构，如红黑树等，它不需要花费过多的精力进行平衡算法，这也是跳跃表的性能优越的一个方面。
  • 跳跃表结构是拿空间换时间的一种结构，尽管空间占用不是很大。
  • 查询、删除，平均时间复杂度都是O(logn)，而插入的平均时间复杂度也是O(logn) 因为涉及到增层操作，所以这里需要注意不是O(n).

 

博客讲解文字较多，推荐一篇以漫画方式讲解跳跃表的博文，更容易理解：《漫画：什么是跳跃表》

此博客为笔者参考网络上各类文章总结性书写，原创手打，如有错误欢迎指正。