【组成原理-数据】浮点数的编码与运算
1 浮点数的格式
浮点数的格式如下:
| 符号 (S) | 阶码 (E) | 尾数 (M) |
|---|---|---|
| 反映浮点数的正负 | 反映浮点数的小数点的实际位置 | 反映浮点数的精度 |
浮点数真值:N = (-1)S * 1.M * 2E-偏置值(E 表示阶码的无符号解释)
1.1 符号 (S)
符号位 S 取值 0 或 1,用来决定浮点数的符号。
1.2 阶码 (E)
阶码或指数 E 是一个二进制定点整数,用 n 位移码表示,其偏置值为2n-1-1,与定点数的移码偏置值相比,多减了 1,区别如下:
| 真值 | 补码 | 定点数的移码 | 浮点数的阶码 | 对应的无符号数 |
|---|---|---|---|---|
| -128 | 1000,0000 | 0000,0000 | 1111,1111 | 255 |
| -127 | 1000,0001 | 0000,0001 | 0000,0000 | 0 |
| -126 | 1000,0010 | 0000,0010 | 0000,0001 | 1 |
| ... | ... | ... | ... | ... |
| -2 | 1111,1110 | 0111,1110 | 0111,1101 | 125 |
| -1 | 1111,1111 | 0111,1111 | 0111,1110 | 126 |
| 0 | 0000,0000 | 1000,0000 | 0111,1111 | 127 |
| 1 | 0000,0001 | 1000,0001 | 1000,0000 | 128 |
| 2 | 0000,0010 | 1000,0010 | 1000,0010 | 129 |
| ... | ... | ... | ... | ... |
| 125 | 0111,1101 | 1111,1101 | 1111,1100 | 252 |
| 126 | 0111,1110 | 1111,1110 | 1111,1101 | 253 |
| 127 | 0111,1111 | 1111,1111 | 1111,1110 | 254 |
1.3 尾数 (M)
尾数 M 是一个二进制定点小数,一般用原码定点小数表示。
由于二进制浮点数要求规格化,因此尾数的最高位总是“1”,为了能使尾数多表示一位,将这个“1”隐藏,称为隐藏位。因此实际上 n 位尾数表示了 n+1 位有效数字。
2 IEEE 754 标准
IEEE 754 标准常用的格式有:短浮点数(单精度)和长浮点数(双精度)。
2.1 短浮点数(float 型)
格式:
| 符号 (S) | 阶码 (E) | 尾数 (M) |
|---|---|---|
| 1 位 | 8 位 | 23 位 |
- 浮点数真值:
N = (-1)S * 1.M * 2E-127(E 表示阶码的无符号解释) - 阶码范围(无符号解释):
1 ≤ E ≤ 254(0 和 255 作为特殊用途,不算其中) - 阶码真值范围:
-126 ≤ E ≤ 127(-128 和 -127 作为特殊用途,不算其中)
【注】尾数位数为 23+1 位,所以数值部分可以表示 24 位精度。
短浮点数的解释
| 符号 | 阶码 | 尾数 | 值 |
|---|---|---|---|
| 0 | 全 0 | 全 0 | +0 |
| 1 | 全 0 | 全 0 | -0 |
| 0 | 全 1(无符号解释:255) | 全 0 | +∞ |
| 1 | 全 1(无符号解释:255) | 全 0 | -∞ |
| 0 | 全 1(无符号解释:255) | 不全为 0 | NaN |
| 1 | 全 1(无符号解释:255) | 不全为 0 | NaN |
| 任意 | 既不全为 0,又不全为 1 | 任意 | 短浮点数 |
| 0 | (无符号解释)1 | 0 | 正数范围的最小值 = +1.0 * 2-126 |
| 1 | (无符号解释)1 | 0 | 负数范围的最大值 = -1.0 * 2-126 |
| 0 | (无符号解释)254 | 全 1 | 正数范围的最大值 = +(2-2-23) * 2127 |
| 1 | (无符号解释)254 | 全 1 | 负数范围的最小值 = -(2-2-23) * 2127 |
【注】当 M 全 0 时尾数取最小值,此时表示的尾数为 1.0;当 M 全 1 时尾数取最大值,即 M = 1 - 2-23,此时表示的尾数为 1 + M = 2 - 2-23。
2.2 长浮点数(double 型)
格式:
| 符号 (S) | 阶码 (E) | 尾数 (M) |
|---|---|---|
| 1 位 | 11 位 | 52 位 |
- 浮点数真值:
N = (-1)S * 1.M * 2E-1023(E 表示阶码的无符号解释) - 阶码范围(无符号解释):
1 ≤ E ≤ 2046(0 和 2047 作为特殊用途,不算其中) - 阶码真值范围:
-1022 ≤ E ≤ 1023(-1024 和 -1023 作为特殊用途,不算其中)
【注】尾数位数为 52+1 位,所以数值部分可以表示 53 位精度。
长浮点数的解释
| 符号 | 阶码 | 尾数 | 值 |
|---|---|---|---|
| 0 | 全 0 | 全 0 | +0 |
| 1 | 全 0 | 全 0 | -0 |
| 0 | 全 1(无符号解释:2047) | 全 0 | +∞ |
| 1 | 全 1(无符号解释:2047) | 全 0 | -∞ |
| 0 | 全 1(无符号解释:2047) | 不全为 0 | NaN |
| 1 | 全 1(无符号解释:2047) | 不全为 0 | NaN |
| 任意 | 既不全为 0,又不全为 1 | 任意 | 长浮点数 |
| 0 | (无符号解释)1 | 0 | 正数范围的最小值 = +1.0 * 2-1022 |
| 1 | (无符号解释)1 | 0 | 负数范围的最大值 = -1.0 * 2-1022 |
| 0 | (无符号解释)2046 | 全 1 | 正数范围的最大值 = +(2-2-52) * 21023 |
| 1 | (无符号解释)2046 | 全 1 | 负数范围的最小值 = -(2-2-52) * 21023 |
【注】当 M 全 0 时尾数取最小值,此时表示的尾数为 1.0;当 M 全 1 时尾数取最大值,即 M = 1 - 2-52,此时表示的尾数为 1 + M = 2 - 2-52。
2.3 相关例题
【例 1】将 (-8.25)10 转换为 IEEE 754 标准下的 32 位单精度浮点数。
化为二进制小数:(-8.25)10 = (-1000.01)2 = (-1.00001)2 * 23
符号位 = 1
尾数 = .00001 (隐含最高位 1)
阶码真值 = 3,阶码的偏移量 = 127D,阶码 = 真值+偏移量 = (3+127)10 = (130)10 = (1000 0010)2(转化为无符号数)
浮点数:1,1000 0010,00001000000000000000000
划分好的浮点数:1100,0001,0000,0100,0000,0000,0000,0000 = C104,0000H
【例 2】将 IEEE 754 标准下的 32 位单精度浮点数 41A4C000H 转换为十进制小数。
划分好的浮点数:41A4C000H = 0100,0001,1010,0100,1100,0000,0000,0000
浮点数:0,1000 0011,01001001100000000000000
符号位 = 0(正数)
尾数 = .010010011(隐含最高位 1)= (1.010010011)2 = (1 + 2-2 + 2-5 + 2-8 + 2-9)10 = (1 + 0.25 + 0.03125 + 0.00390625 + 0.001953125)10 = (1.287109375)10
阶码 = (1000 0011)2 = (131)10(视为无符号数),阶码的偏移量 = 127D,阶码真值 = 131-127 = 4
十进制小数 = 1.287109375 * 24 = 20.59375
【例 3】已知浮点数格式如下:阶码、尾数均用补码表示,且位数分别为 5 和 7(均含 2 位符号位,即 2 位阶符,2 位数符)。将 X = 27*29/32 和 Y = 25*5/8 化为浮点数。
【X】阶码真值 = 7,补码 = 111,阶码 = 00.111
尾数 = 29/32 = 16/32 + 13/32 = 16/32 + 8/32 + 5/32 = 16/32 + 8/32 + 4/32 + 1/32 = 1/2 + 1/4 + 1/8 + 1/32 = 2-1 + 2-2 + 2-3 + 2-5
所以尾数 = 00.11101
所以 X 的浮点数 = 00.111,00.11101
【Y】阶码真值 = 5,补码 = 101,阶码 = 00.101
尾数 = 5/8 = 4/8 + 1/8 = 1/2 + 1/8 = 2-1 + 2-3
所以尾数 = 00.10100
所以 Y 的浮点数 = 00.101,00.10100
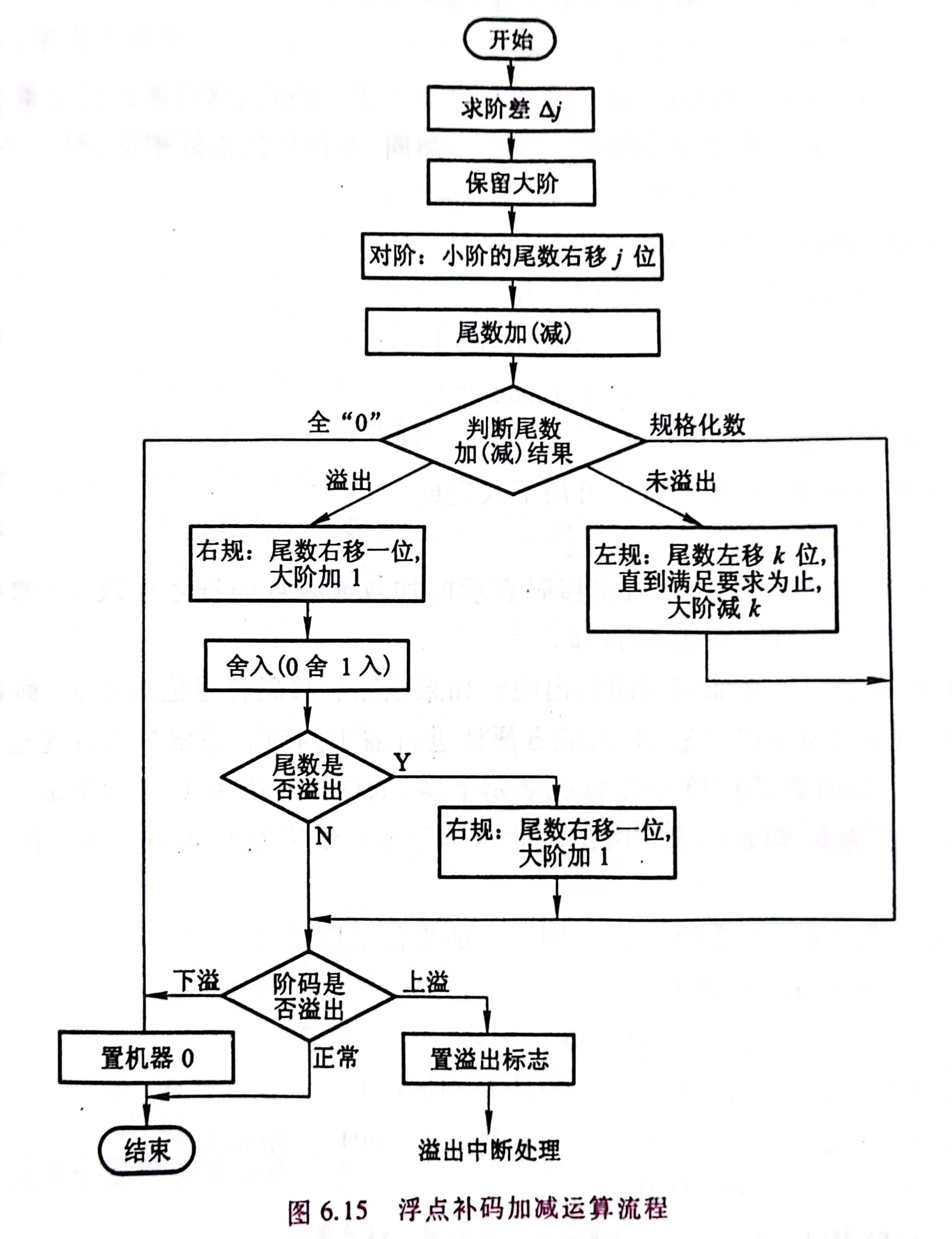
3 浮点数的加减运算
浮点数加减运算的步骤为:
- 对阶
- 尾数求和
- 规格化
- 舍入
- 溢出判断
(参考资料:浮点加减运算之0舍1入法与恒置1法)
3.1 对阶
为了使两操作数的小数点对齐,需要让两个操作数的阶码相等,小阶向大阶看齐,尾数需要右移,相应地,阶码需要加上右移的次数(不同编码对应不同的右移规则,请参考 3.3 节的规格化操作)。其原理与我们进行科学计数法的加减运算是一致的。
尾数多次右移时,可能会发生精度丢失,为尽可能保留精度,需要进行舍入。请参考 3.4 节中的三种舍入方法。
【例】两个阶码和尾数均用补码表示的浮点数:x = 00.01,00.1101,y = 00.11,11.0110,请进行对阶操作。
【解】显然 x 的阶数更小,y 的阶数更大,需要与 y 对齐。
x 与 y 阶码相差:00.11 - 00.01 = 00.10,该补码对应真值为 2,表示 x 的尾数需要右移两次。
x 右移两次,阶码加 2 后:x = 00.11,00.0011(保留位:01),此时需要进行后续的舍入操作。
3.2 尾数求和
对阶后的两个尾数按定点数加减运算规则进行运算。
3.3 规格化
尾数求和完毕后,检查尾数是否符合规格。不满足要求的尾数需要规格化,即左规或右规操作。注意规格化操作不包含符号位(双符号位中的低符号位参与移位)。
3.3.1 单符号位原码尾数的规格化
规格化原码尾数的小数点前是符号位,小数点后的第一位(即尾数最高位)一定是 1。
- 规格化原码的正尾数为
0.1x···x - 规格化原码的负尾数为
1.1x···x - 原码尾数规格化时,无论正数还是负数,左规和右规后的空位均补 0
【注】基数为 4 的原码规格化的尾数最高两位不全为 0。
【例】尾数用原码表示的浮点数为 0011111,1.0111···01,则该数需要规格化吗?
【解】因为尾数为 1.0111···01,原码为负,小数点两边应全为 1,所以需要规格化。
将尾数左移一位,阶码减 1,结果为 0100000,1.111···010。
3.3.2 单符号位补码尾数的规格化
规格化补码尾数的符号位和尾数最高位是否相反,若是,则为规格化浮点数。
- 规格化补码的正尾数为
0.1x···x - 规格化补码的负尾数为
1.0x···x - 补码正尾数规格化时,左规和右规后的空位均补 0
- 补码负尾数规格化时,左规后的空位补 0,右规后的空位补 1
【例】尾数用补码表示的浮点数为 25 * 1.10101,则该数需要规格化吗?
【解】因为尾数为 1.10101,小数点两边符号相同,所以需要规格化。
将尾数左移一位,阶码减 1,结果为 24 * 1.01010。
3.3.3 双符号位补码尾数的规格化(常考)
双符号补码位尾数的格式为00.1x···x或11.0x···x,在进行尾数运算(此时需化为双符号位补码尾数)时,可能会出现不符合的尾数,需要进行以下处理:
- 右规:形如
01.x···x或10.x···x的尾数,此时尾数溢出,需要右移一位,变为:0.x···x或1.x···x,最后补上双符号位的高位:00.x···x或11.x···x。只需右移一位,阶码加 1
【注】右规后,可能会出现形如
00.0···01x···x或11.1···10x···x的尾数,需要再进行左规操作
- 左规:形如
00.0···01x···x或11.1···10x···x的尾数,需要不断左移,直到变为:00.1x···x或11.0x···x。每左移一位,阶码减 1
【注】双符号位浮点数规格化的几个要点:
- 双符号位中,只有低符号位需参与移位运算,而高符号位不动。因为只有高符号位表示该数真正的符号,低符号位用来指示溢出信息。
- 右规后被移去的低位需要暂时保留下来,称为保留位(勿吐槽,这个名字是我自己起的),参与下面的舍入操作。
- 区分左规和左移、右规和右移:左规包含一次或多次左移操作,右规一般只包含一次右移操作。
【例】规格化:11.100,10.110001000
【解】尾数格式为“10.x···x”,说明尾数溢出,需要进行右规操作。
- 原来的浮点数:11.100,10.110001000
- 尾数右移一位,阶码加 1,并注明保留位:11.101,11.011000100(保留位:0)
- 尾数双符号位补全:11.101,11.011000100(保留位:0)
- 现该数符合要求,无需进行另外的左规操作
3.4 舍入
- 右规后被移去的低位需要暂时保留下来,称为保留位(勿吐槽,这个名字是我自己起的),参与舍入操作。
- 对阶以后也需要进行舍入。请注意:
- 不是每右移一次就进行舍入,而是多次右移直到符合格式后才进行舍入操作。
- 在对阶中,可能需要多次右移操作,则保留位可能有多位。
- 舍入的方法:
- 截断法:不管保留位是多少,舍去保留位。
- 恒置 1 法:不管保留位是多少,尾数末位直接置 1,舍去保留位。
- 0 舍 1 入法:若保留位的最高位是 1,则尾数加 1,然后舍去保留位(加 1 操作可能会使尾数溢出,需要再一次右规);如果是 0,则直接舍去保留位。
- 舍入的概念仅在浮点数适用。
- 浮点数舍入只发生在对阶和右规操作。对阶时,尾数右移,此时就会产生舍入;同理,右规即右移,也会产生舍入。
- 舍入不一定产生误差,是否产生误差与舍入的方法和尾数的特点有关。
(参考资料:计算机组成原理(七))
【例 1】以下浮点数已完成对阶,请进行舍入操作:
(1)11.101,11.01101(保留位:10);(2)11.101,11.01100(保留位:00)
【解】保留位有两位,则只有最高位参与舍入。有三种方法舍入:
- 截断法:(1)11.101,11.01101;(2)11.101,11.01100
- 恒置 1 法:(1)11.101,11.01101;(2)11.101,11.01101
- 0 舍 1 入法:(1)11.101,11.01110;(2)11.101,11.01100
【例 2】以下浮点数已完成规格化,请进行舍入操作:
(1)11.101,11.01101(保留位:0);(2)11.101,11.01011(保留位:1)
【解】三种方法舍入:
- 截断法:(1)11.101,11.01101;(2)11.101,11.01011
- 恒置 1 法:(1)11.101,11.01101;(2)11.101,11.01011
- 0 舍 1 入法:(1)11.101,11.01101;(2)11.101,11.01100
3.5 溢出判断(直接看阶码)
- 溢出分为尾数溢出和阶码溢出,阶码溢出分为阶码上溢和阶码下溢
- 阶码上溢(阶码全 1):可能发生在右规和尾数舍入
- 右规导致阶码加 1,可能发生阶码上溢
- 尾数若采用 0 舍 1 入法,则有可能导致尾数加 1 溢出,需要右规。右规后阶码加 1,可能发生上溢
- 阶码下溢(阶码全 0):可能发生在左规,因为左规导致阶码减 1,可能发生下溢
由此可见,尾数溢出可以由右规操作得到纠正,溢出的问题转移到阶码上。所以,看一个运算结果是否溢出,就需要看阶码是否溢出。在实际情况下,浮点数的阶码下溢一般视作运算结果为 0,因而浮点数的溢出都由阶码上溢造成。
- 尾数溢出:结果不一定溢出,如向下舍入 11.00 到 11.0 是没有误差的
3.6 相关例题
【例】浮点数格式如下:阶码、尾数均用补码表示,且位数分别为 5 和 7(均含 2 位符号位,即 2 位阶符,2 位数符)。已知 X = 27*29/32 和 Y = 25*5/8 ,求浮点运算 X+Y。
【0. 化为浮点数】X 的浮点数 = 00.111,00.11101,Y 的浮点数 = 00.101,00.10100(见 2.3 节)
【1. 对阶】Y 的阶码更小,需要进行右规两次:Y = 00.111,00.00101
【2. 尾数相加】X + Y = 00.11101 + 00.00101 = 01.00010
【3. 规格化】00.111,01.00010 -->(尾数溢出,需右规)01.000,00.10001(保留位:0)
【4. 舍入】保留位为 0,说明没有发生精度丢失,直接丢弃保留位:01.000,00.10001
【5. 溢出判断】阶码符号位为 01,说明发生了溢出


 浙公网安备 33010602011771号
浙公网安备 33010602011771号