Codeforces Global Round 13 题解（A-D)

A. K-th Largest Value

题目大意：

给出一个含有\(n\)个整数的数组，整数的取值只有0和1。处理\(q\)次询问，格式如下：

\(1\) \(x\) ：将\(a_x\)变成\(1-a_x\)
\(2\) \(k\) ：输出数组中第k大的整数

解题思路：

第一眼看到是求数组第k大的整数，以为是很棘手的题目。后来仔细一想数组中只有0和1，那么输出的结果就只有0和1，所以只要记录一想数组中0和1的个数，每次询问的时候判断一下数组中1的个数是否大于等于k，大于等于k就输出1，否则就输出0。

代码如下：

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1e5+10;
int a[maxn],num[2];
int n,q;
int main()
{
	scanf("%d%d",&n,&q);
	int n0=0,n1=0;
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		num[a[i]]++;
	}
	while(q--){
		int op,x;
		scanf("%d%d",&op,&x);
		if(op==1){
			num[a[x]]--;
			num[1-a[x]]++;
			a[x]=1-a[x];
		}
		else
		{
			if(x>num[1]) puts("0");
			else puts("1");
		}
	}
	return 0;
}

B. Minimal Cost

题目大意：

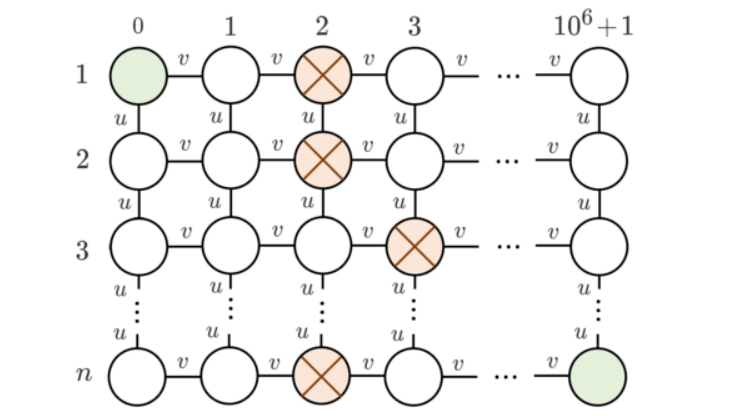
给出一张二维图形，\(n\)行\(10^6+2\)列，如下图所示。每一行都会有一个障碍，第\(i\)行的障碍位于\(（i,a_i）\)，其中\(1\le a_i\le 1e6\)。

因为在移动的时候不能够穿过障碍，所以现在想通过移动某些障碍使得能从\((1,0)\)走到\((n,10^6+1)\)。障碍只能移到原本没有障碍的位置上，也不能移动到边界外面，可以花费\(u\)枚硬币将障碍上下移动,花费\(v\)枚硬币左右移动。问最少需要花费多少硬币才能从\((1m0)\)走到\((n,10^6+1)\)。

解题思路：

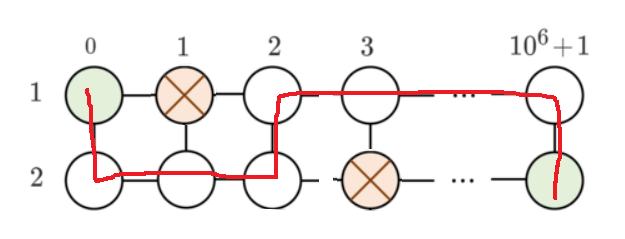
注意观察\(1\le a_i\le 1e6\)，所以我们不会出现被障碍局限在某个区域内的情况，我们可以到达每一个障碍的左侧。因为每一行都有一个障碍，所以我们可以将所有的障碍看成一张包围网，只要移动其中某一个障碍出现缺口就可以突出重围。我们可以将两个障碍看成一个整体来考虑，可以分成一下三种情况

\(|a_i-a_{i+1}|>1\),这种情况下我们是可以直接绕过障碍到达终点的，\(cost=0\)。
\(|a_i-a_{i+1}|=1\),这种情况下我们可以选择将其中一个左右移动或者上下移动，\(cost=\min(u,v)\)。
\(|a_i-a_{i+1}|=0\),这种情况下我们需要选择一个障碍进行左右移动和上下移动，或者连续两次左右移动,\(cost=\min(u+v,v+v)\)。

枚举一下取最小值就是答案。

代码如下：

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=110;
int T,n,u,v;
int a[maxn];
int main()
{
	scanf("%d",&T);
	while(T--){
		scanf("%d %d %d",&n,&u,&v);
		for(int i=1;i<=n;i++) scanf("%d",&a[i]);
		int res=2e9;
		for(int i=1;i<n;i++){
			if(abs(a[i]-a[i+1])>1){
				res=0;
				break;
			}
			else{
				if(a[i]==a[i+1]) res=min(res,min(u+v,v+v));
				else res=min(res,min(u,v));
			}
		}
		printf("%d\n",res);
		
	}
	return 0;
}

C. Pekora and Trampoline

题目大意：

有\(n（1\le n\le 5000)\)个蹦床排成一行，第\(i\)个蹦床的强度为\(s_i\)。如果跳上第\(i\)个蹦床，蹦床会将他弹到\(i+s_i\)并且\(s_i\)会变成\(max(s_i-1,1)\)。换句话说，蹦床使用过后\(s_i\)会减一，最小减到1为止。如果\(i+s_i\)的位置没有蹦床，则此回合结束，否则会一直按照上述规则进行下去，直到他跳到大于\(n\)的位置。问最少需要多少次，可以将所有蹦床的强度变成1。

解题思路：

按照贪心的策略，我们每次肯定是选择从开始位置起第一个\(s_i>1\)的蹦床进行当前回合，但是这种做法的时间复杂度是\(O(n^3)\)，肯定是行不通的。我们通过观察题目可以发现，任何一个\(s_i>1\)的蹦床在\(si\)降为1之前都至少会蹦\(s_i-1\)次，因此在\([i+2,i+s_i]\)区间中的所有蹦床都会被蹦一次。除此之外如果一个蹦床在\(s_i=1\)之后再次被经过，同样会增加下一个蹦床的使用次数。

因为一个蹦床不会被之后的蹦床所影响，所以我们可以从前往后进行遍历。记\(c_i\)为当前蹦床从之前蹦床蹦过来的次数，如果\(c_i<(s_i-1)\)那么，说明当前蹦床还额外需要\(s_i-1-c_i\)次，并且将\(c_j++\),其中\(j\in [i+2,i+s_i]\)。还要记得考虑当\(c_i>(s_i-1)\)的情况，在这种情况下，会在\(s_i=1\)的情况下蹦\(c_i-(s_i-1)\)次，那么\(c_(i+1)\)要加上\(c_i-s_i+1\)。整个做法的时间复杂度是\(O(n^2)\)。

代码如下：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
const int maxn=5e3+10;
int a[maxn],c[maxn];
int T,n;
int main()
{
	scanf("%d",&T);
	while(T--){
		scanf("%d",&n);
		for(int i=0;i<n;i++) scanf("%d",&a[i]);
		memset(c,0,sizeof c);
		LL ans=0;
		for(int i=0;i<n;i++){
			ans+=max(0,a[i]-1-c[i]);
			for(int j=i+2;j<min(n,i+a[i]+1);j++) c[j]++;
             c[i+1]+=max(0,c[i]-a[i]+1);
		}
		printf("%lld\n",ans);
	}
	return 0;
}

D. Zookeeper and The Infinite Zoo

题目大意：

给出一张含有无限个点的图，当且仅当\(u\And v=v\)的时候有一条\(u\)连向\(u+v\)的有向边。一共有\(q\)次询问，对于第\(i\)次询问，问从\(u_i\)经过若干条有向边能否走到\(v_i\)，能的话输出"YES"，否则输出"NO"。数据范围：\(1\le q\le10^5,1\le u_i,v_i\le 2^{30}\).

解题思路：

首先我们可以发现，对于某个整数\(u\)，如果\(u=2^{a_1}+2^{a_2}+\cdots +2^{a_k}\)，那么能满足\(u\And v=v\)的\(v\)一定是由集合\(\{2^{a_1},2^{a_2},\cdots ,2^{a_k}\}\)中若干个数相加得到，例如\(11=(1011)_2\)存在\(11\And1=1\)、\(11\And2=2\)、\(11\And8=8\)、\(11\And3=3\)、\(11\And9=9\)、\(11\And10=10\)、\(11\And11=11\)。

并且我们可以发现，从\(u\)到\(u+v\)的过程中，二进制表示中1的个数不会增加，要么减少（意味着进行了连续的进位，例如\(3=>4\)),要么不变（意味着只进了一位，从低位移动到高位，例如\(3=>5\)）。

所以我们发现只有同时满足以下三种条件的才能从\(u_i\)走到\(v_i\)：

\(u_i\ge v_i\)，因为\(u\)只能走到\(u+v\)，所以\(u\)不能走到比自己更小的点。
\(a\ge b\)，其中\(a,b\)分别表示\(u_i,v_i\)二进制中1的个数，因为从\(u\)到\(u+v\)的过程中二进制1的个数无法增加。
在\(v_i\)二进制中每一个\(1\)都能在\(u_i\)中找到一个更低位或者相同位的\(1\)，因为在移动过程中，对于\(u_i\)中的每一个1无法降位，只能选择进位或者保持不变。

代码如下：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int q,u,v;
int main()
{
	scanf("%d",&q);
	while(q--){
		scanf("%d%d",&u,&v);
		if(u>v){
			 puts("NO");
			 continue;
		}
		vector<int> v1,v2;
		for(int i=0;i<30;i++){
			if(u&1<<i) v1.push_back(i);
			if(v&1<<i) v2.push_back(i);
		}
		if(v1.size()<v2.size()){
			puts("NO");
			continue;
		}
		bool flag=true;
		for(int i=0;i<v2.size();i++)
			if(v1[i]>v2[i]){
				flag=false;
				break;
			}
		puts(flag?"YES":"NO");
	}
	return 0;
}

posted @ 2021-03-02 22:00 陌默丶阅读(60) 评论(0) 收藏举报

刷新页面返回顶部

Codeforces Global Round 13 题解（A-D)