【DFS】树的重心

【题目描述】

给定一颗树，树中包含 n 个结点（编号 1∼n）和 n−1 条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

【输入格式】

第一行包含整数 n，表示树的结点数。

接下来 n−1 行，每行包含两个整数 a 和 b，表示点 a 和点 b 之间存在一条边。

【输出格式】

输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。

【数据范围】

1≤n≤10⁵

【输入样例】

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

【输出样例】

4

 

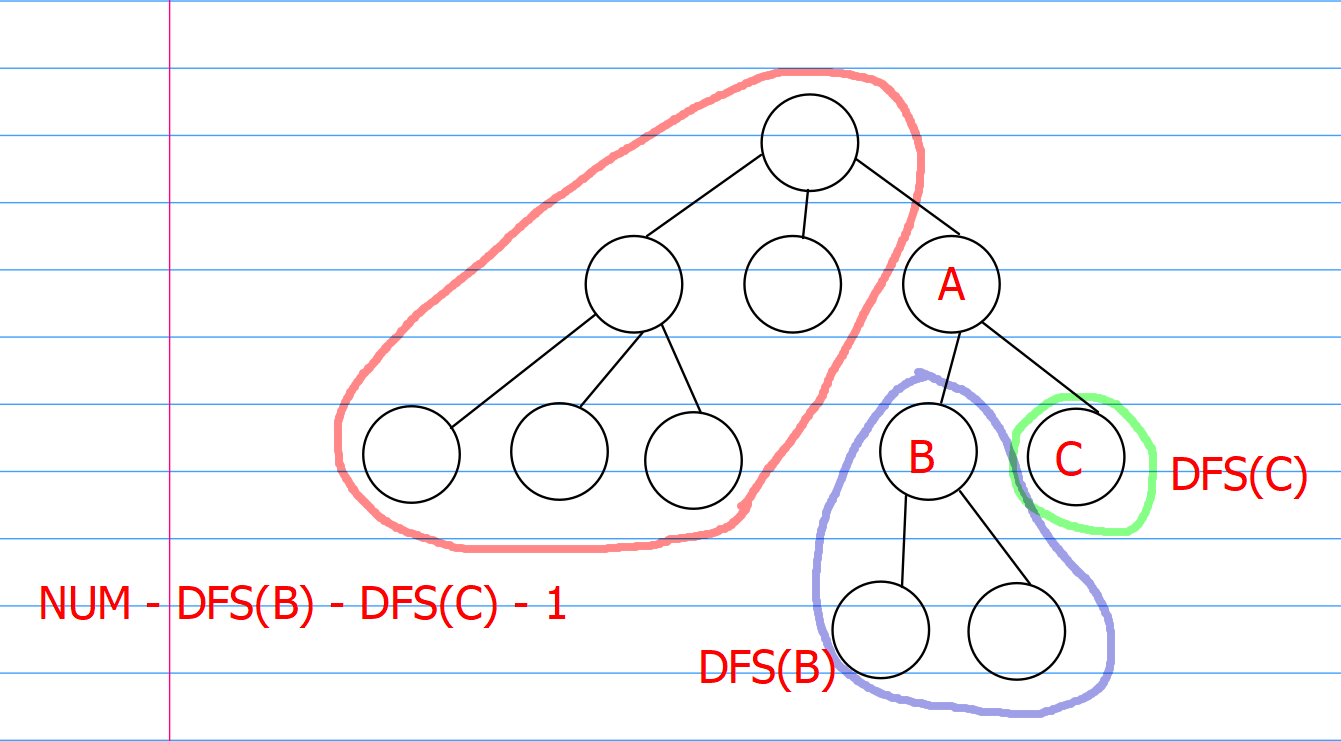
思路：计算出树中所有结点被删去后剩下的连通块的节点数，在其中找出连通块最大值的最小值来。

　　　统计每个结点的连通块最大值，可以首先DFS计算结点A的每个子树结点个数，对于A的父结点连通块的节点个数，可以使用结点总数num减去结点A以及所有结点A的子树结点个数。

 

 

#include <iostream>
#include <string.h>
using namespace std;

const int N = 100009;
int h[N],e[2*N],ne[2*N],idx,st[N];
int ans = 1e9;
int n;
void add(int a,int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int dfs(int u)
{
    int sum = 1,res = 0;
    for(int i = h[u];i != -1;i = ne[i])
    {
        int j = e[i];
        if(!st[j])
        {
            st[j] = 1;
            int s = dfs(j);
            res = max(res,s);
            sum += s;
        }
    }
    res = max(res,n - sum);
    ans = min(ans,res);
    return sum;
}

int main()
{
    memset(h,-1,sizeof h);
    cin >> n;
    for(int i = 0;i < n - 1;++i)
    {
        int a,b;
        cin >> a >> b;
        add(a,b);
        add(b,a);
    }
    dfs(1);
    cout << ans << endl;
    return 0;
}