差分

一维差分

输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数l，r，c，表示一个操作。

输出格式

共一行，包含 n 个整数，表示最终序列。

数据范围

1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000

输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

 

对于差分只需要构造b_n，使得∑b_n=a_n即可，即a数组是b数组的前缀和。

即：b₁ = a₁

　　b₂ = a₂ - a₁

　　b₃ = a₃ - a₂

　　......

　　b_n = a_n - a_n-1

因此，只要有b数组，就可以在O(N)时间内得到a数组。

 

差分数组b的作用就可以实现使得数组a在[l,r]区间内加上c的操作，假设让b_l加上c，那么从a_l到a_n都会加上c，因为使用b_i数组求a_i的时候是使用b₁~b_i累加求出来的。

故对于要在数组a[l,r]区间上实现加c的操作，只需要从b_l加上c，然后从b_r+1的位置减去c即可。

 

#include <iostream>
using namespace std;
const int N = 100009;
int a[N],b[N];
void insert(int l,int r,int c)
{
    b[l] += c;
    b[r + 1] -= c;
}
int main()
{
    int n , m;
    cin >> n >> m;
    for(int i = 1;i <= n;++i)
    {
        cin >> a[i];
        insert(i,i,a[i]);
    }
    while(m--)
    {
        int l,r,c;
        cin >> l >> r >> c;
        insert(l,r,c);
    }
    for(int i = 1;i <= n;++i)
    {
        b[i] += b[i-1];
        cout << b[i] << " ";
    }
    return 0;
}

 

 

 

---

 

二维差分矩阵

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

 

 

 

 

 

 

 

案发时发生简单快捷

矩阵差分比较麻烦，因为是二维，因此b数组比较难以构造，但是先抛开b数组是什么样的形式，假设b数组的前缀和就是a，是已知的，那么接下来来看看是如何实现大矩阵中小矩阵块的操作。

 

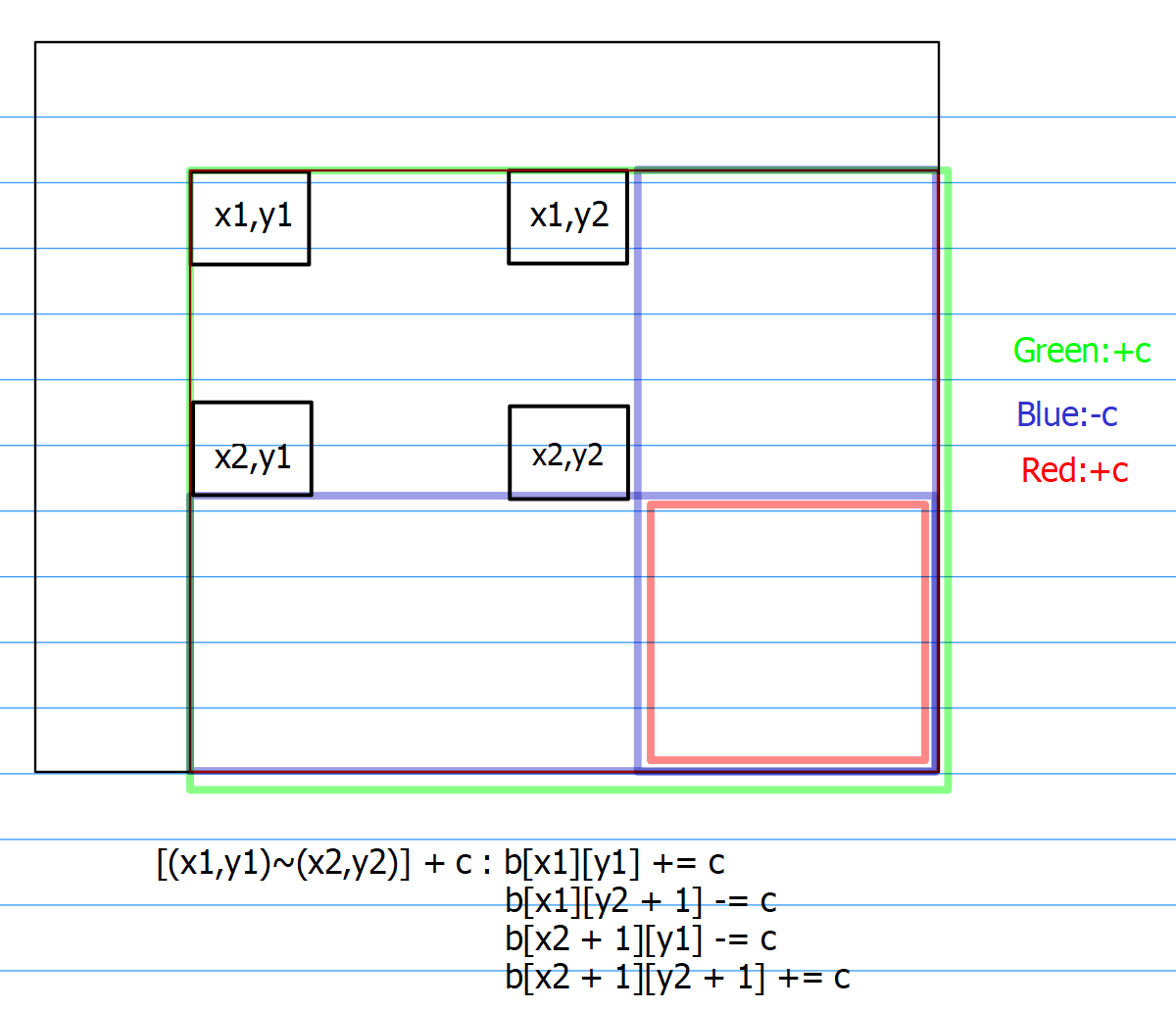
 知道了如何操作之后，其实如何构造b数组已经不重要了，只需要像一维差分中的insert一样利用这一个操作过程，即可实现b数组的构造。

至于a数组的求值参考二维的前缀和即可。

#include <iostream>
using namespace std;
const int N = 1009;
int a[N][N],b[N][N];

void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -=c;
    b[x1][y2 + 1] -=c;
    b[x2 + 1][y2 + 1] +=c;
}

int main()
{
    int n,m,q;
    cin >> n >> m >> q;
    for(int i = 1;i <= n;++i)
    {
        for(int j = 1;j <= m;++j)
        {
            cin >> a[i][j];
            insert(i,j,i,j,a[i][j]);
        }
    }

    while(q--)
    {
        int x1,y1,x2,y2,c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1,y1,x2,y2,c);
    }
    
    for(int i = 1;i <= n;++i)
    {
        for(int j = 1;j <= m;++j)
        {
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
            cout << b[i][j] << " ";
        }
        cout << endl;
    } 
    return 0;
}