逆序对的数量

【题目描述】

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第  i 个和第  j  个元素，如果满足 i<j 且 a[i]>a[j]，则其为一个逆序对；否则不是。

【输入格式】

第一行包含整数 n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

【输出格式】

输出一个整数，表示逆序对的个数。

【数据范围】

1≤n≤100000，
数列中的元素的取值范围 [1,109]。

【输入样例】

6

2 3 4 5 6 1

【输出样例】

5

分治策略一般分为拆分，求解，合并三个过程；本题利用归并排序过程中的合并过程。

 

 

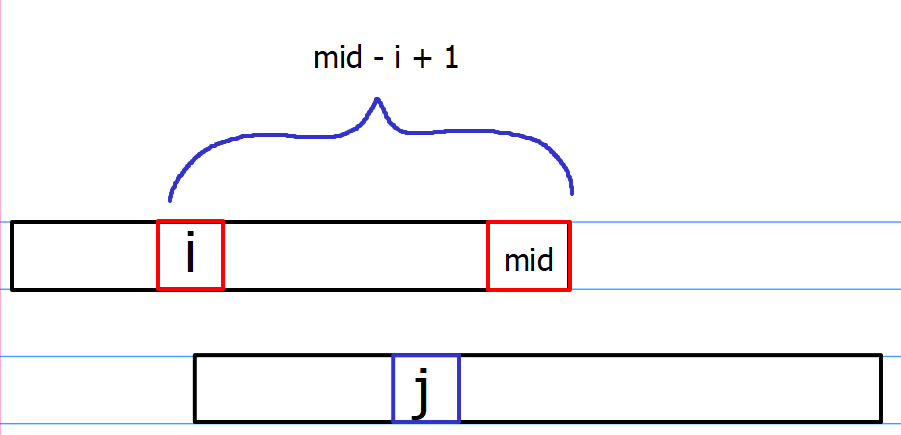
 由于归并排序合并过程中，两个待合并数组已然有序，因此可以利用这种“有序”来计算逆序对的数量。

当前半部分走到i，后半部分走到j时，假设num[i] > num[j]，那么就意味着从i到mid的位置的所有数num[i~mid]都大于num[j]，构成了一对逆序对，因此通过计算从i到mid共有mid - i + 1个数，即可知道当前状态下的逆序对。

 

#include <iostream>
using namespace std;
const int N = 100009;
int num[N],tmp[N],n;
long long res;

long long mergeSort(int l,int r)
{
    if(l >= r)
        return 0;
    int mid = l + r >> 1;
    res = mergeSort(l,mid) + mergeSort(mid + 1,r);
    
    int i = l,j = mid + 1, k = 0;
    while(i <= mid && j <= r)
    {
        if(num[i] <= num[j])
            tmp[k++] = num[i++];
        else
        {
            tmp[k++] = num[j++];
            res += mid - i + 1;
        }
    }
    while(i <= mid)
        tmp[k++] = num[i++];
    while(j <= r)
        tmp[k++] = num[j++];
    for(int i = l,j = 0;i <= r;++i,++j)
        num[i] = tmp[j];
    return res;
}

int main()
{
    cin >> n;
    for(int i = 0;i < n;++i)
        cin >> num[i];
    cout << mergeSort(0,n-1) << endl;
    return 0;
}