【树形DP】打家劫舍III

【题目链接】

打家劫舍III

【题目描述】

在上次打劫完一条街道之后和一圈房屋后，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。 除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。

计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。

【输入输出样例】

输入: [3,2,3,null,3,null,1]

　　3
　　/ \
　  2 3
　　\  \
　　3 1

输出: 7

【数据范围】

1 <= nums.length <= 100
0 <= nums[i] <= 400

 

对于每一个结点，都有两种决策，偷或者不偷，而且父子结点之间又存在一定的牵制关系（相邻房屋不能同一晚上偷窃），因此需要建立二维的状态表示，f[i][2]

f[i][0] 表示不偷第i个房屋

f[i][1]表示偷窃第i个房屋

 

对于当前结点A，如果选择偷窃当前结点A，那么它的左右孩子BC一定不能被选择，因此当前结点A所能偷到的最高金额就取决于左右孩子BC不偷的金额，即f[A][1] = f[B][0] + f[C][0] + money[A];

 

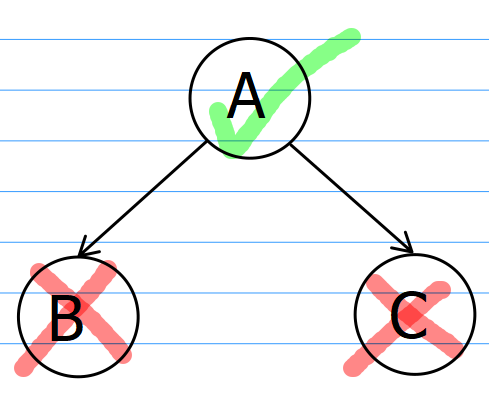
如果选择不偷窃当前结点A，那么它的最高金额就取决于左右孩子BC被偷窃的金额，但需要注意，不偷窃A并不代表一定就偷窃B和C，因此需要在偷窃BC以及不偷窃BC中寻找最大值，即f[A][0] += max(f[B][0],f[B][0]) + max(f[C][0],f[C][1]);

 

 

 

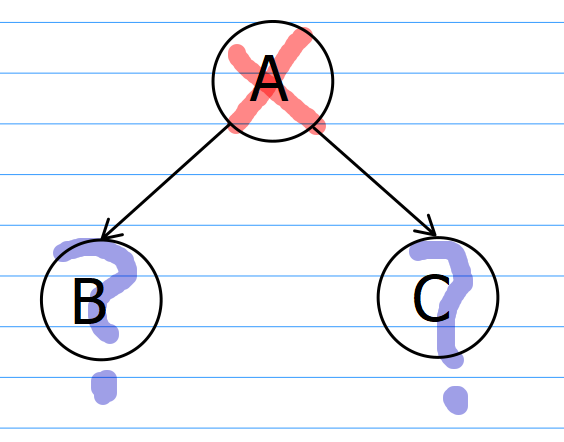
综合以上两种决策，选择出最大金额的决策即可。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Solution {
public:
    void dfs(TreeNode* node)
    {
        go[node] = node->val;
        no[node] = 0;
        if(nullptr != node->left) 
            dfs(node->left);
        no[node] += max(no[node->left],go[node->left]);
        go[node] += no[node->left];
        if(nullptr != node->right) 
            dfs(node->right);
        no[node] += max(no[node->right],go[node->right]);
        go[node] += no[node->right];  
    }
    int rob(TreeNode* root) {
        dfs(root);
        return max(go[root],no[root]);
    }
    map<TreeNode*,int> go;
    map<TreeNode*,int> no;
};