【数位DP】不降数

【题目链接】

不降数

【题目描述】

定义一种不降数，这种数字必须满足从左到右各位数字成小于等于的关系，如123，446。现在大家决定玩一个游戏，指定一个整数闭区间[a,b] ，问这个区间内有多少个不降数。

【输入】

有多组测试数据。每组只含两个数字 a，b意义如题目描述。1≤a,b≤2³¹。

【输出】

每行给出一个测试数据的答案，即 [a,b] 之间有多少不降数。

【输入样例】

　　1 9

　　1 19

【输出样例】

　　9

　　18

 

数位DP通常是需要按位分情况讨论的，将数num划分为a_na_n-1...a₂a₁，从最高位开始到低位，划分为0~a_i-1与a_i，如果第i位上填的是0~a_i-1，那么后面的所有位数都可以填0~9，如果第i位是a_i，那么就继续往下讨论下一位，通过这种划分方式，可以保证我们枚举的数不超过num。

此外需要结合前缀和的思想，即求区间[a,b]的不降数个数可转化为求count(b) - count(a - 1)的值。

举例：352

　　　首先枚举最高位，那么分别就是 0XX、1XX、2XX，

　　　接下来枚举次高位，30X、31X、32X、33X、34X,

　　　再继续枚举最低为，350、351，

　　　到最后一个数352特判一下是不是不降数就可以了（X的位置可以填0~9）。

 

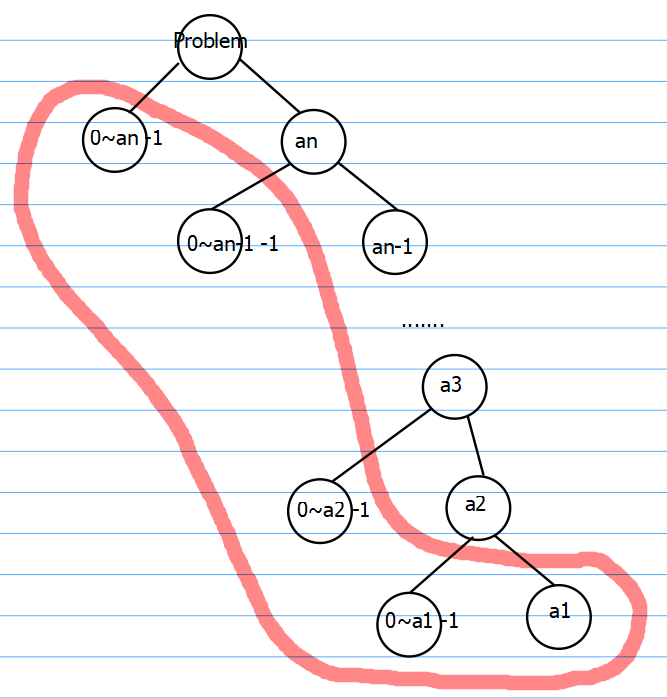
那么答案就在我们所画的红框内部，此外，不降数的个数，应当与 数的位数 还有 数的最高位 有关，因此我们可以使用状态 f[i][j] 来表示  位数为i位，且最高位为j的数字的  不降数个数。

状态表示已经解决，那么接下来就思考如何进行状态的计算。

对于一个i位数，最高位为j的数字，表示形式如下

　　　　　　　　　　　　　　　　　　　　j　　k　　x　　x　　x　　...　　x

如果这个数字是不降数，那么次高位k就应当满足k≥j，故到此可以得出状态转移方程：f[i][j] = f[i - 1][j] + f[i - 1][j + 1] + f[i - 1][j + 2] + ....... + f[i - 1][9]；

for(int i = 0;i <= 9;++i)　　//初始化1位数的情况，f[1][0]也是一个不降数
    f[1][i] = 1;
for(int i = 2;i <= N;++i)　　//枚举位数i
    for(int j = 0;j <= 9;++j)//枚举首位数字j
        for(int k = j;k <= 9;++k)//枚举次高位数字k
            f[i][j] += f[i - 1][k];

至此，就完成位数为i位，最高位为j的数字中不降数个数的预处理。接下来，按最开始的思想，从最高位开始，枚举每一位数字的不降数并累加得出答案。

　　　　

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 12;
int f[N][N];
int num[N];
int count(int n)
{
    if(n == 0)
        return 1;
    int cnt = 0;
    while(n)
    {
        num[++cnt] = n % 10;
        n /= 10;
    }
    int res = 0;
    int now = 0,last = 0;
    for(int i = cnt;i > 0;--i)
    {
        now = num[i];
        for(int k = last;k < now;++k)　　//枚举ai~ai-1,当枚举到ai则直接跳往下一位
            res += f[i][k];
        if(last > now)　　//当上一位比当前位大时，就没有继续计算的必要了，如5228，到第二位时，5 > 2，必不可能成为不降数
            break;
        last = now;
        if(i == 1)　　//特判最后一位
            ++res;
    }
    return res;
}

int main()
{
    for(int i = 0;i <= 9;++i)
        f[1][i] = 1;
    for(int i = 2;i <= N;++i)
        for(int j = 0;j <= 9;++j)
            for(int k = j;k <= 9;++k)
                f[i][j] += f[i - 1][k];
    int n,m;
    while(cin >> n >> m)
        cout << count(m) - count(n - 1) << endl;
    return 0;
}