ABC282Ex Min + Sum

两只 \(\log\) 跑得快，序列分治真可爱。

洛谷 AT

• 给出两个长为 \(n\) 的序列 \(a,b\) 和常数 \(S\)，求有多少个区间 \([l,r]\,(1\le l\le r\le n)\)，满足：

  \[\min\limits_{i=l}^r a_i+\sum_{j=l}^rb_j\le S \]

• \(n\le 2\times 10^5\)。

考虑分治。设当前分治区间为 \([l,r]\)，分治中点 \(mid=\left\lfloor\dfrac{l+r}{2}\right\rfloor\)。

考虑如何统计跨过中点的区间个数。枚举左端点 \(i\)，同时记录 \(s=\sum\limits_{x=i}^{mid}b_x\) 和 \(minn=\min\limits_{y=i}^{mid} a_y\)。求出有多少个合法的右端点 \(j\)。

对于 \((mid,r]\) 这部分区间的所有 \(j\)，预处理 \(sum_j=\sum\limits_{u=mid+1}^j b_u\)，\(pre_j=\min\limits_{v=mid+1}^j a_v\)。

把右端点 \(j\) 分成两种，分别统计：

• \(pre_j\ge minn\)，则符合条件的区间满足 \(s+sum_j+minn\le S\)，那么统计有多少 \(j\) 满足 \(sum_j\le S-s-minn\)。

• \(pre_j< minn\)，则符合条件的区间满足 \(s+sum_j+pre_j\le S\)，那么统计有多少 \(j\) 满足 \(sum_j+pre_j\le S-s\)。

考虑从右往左枚举左端点 \(i\)，不难发现可以找到一个分界点 \(\boldsymbol k\) 使得当 \(\boldsymbol{j\in (mid,k)}\) 时，区间满足第一种情况；当 \(\boldsymbol{j\in[k,r]}\) 时，区间满足第二种情况。且随着 \(\boldsymbol{i}\) 的减小，\(\boldsymbol k\) 单调不降。

使用平衡树 \(t_1,t_2\) 分别维护 \((mid,k)\) 中 \(sum_j\) 的权值集合和 \([k,r]\) 中 \(sum_j+pre_j\) 的权值集合。分界点 \(k\) 右移时（接下来的 \(k\) 是右移前的 \(k\)），在 \(t_1\) 中插入 \(sum_k\)，在 \(t_2\) 中删除 \(sum_k+pre_k\)。可以完成⌈查询集合内有多少数不超过某个定值⌋这个操作。

有人可能会说平衡树小题大做，但是 __gnu_pbds::tree 真的很方便。

时间复杂度为 \(\mathcal{O}(n\log^2 n)\)，空间复杂度为 \(\mathcal{O}(n)\)。

评测记录（含代码）

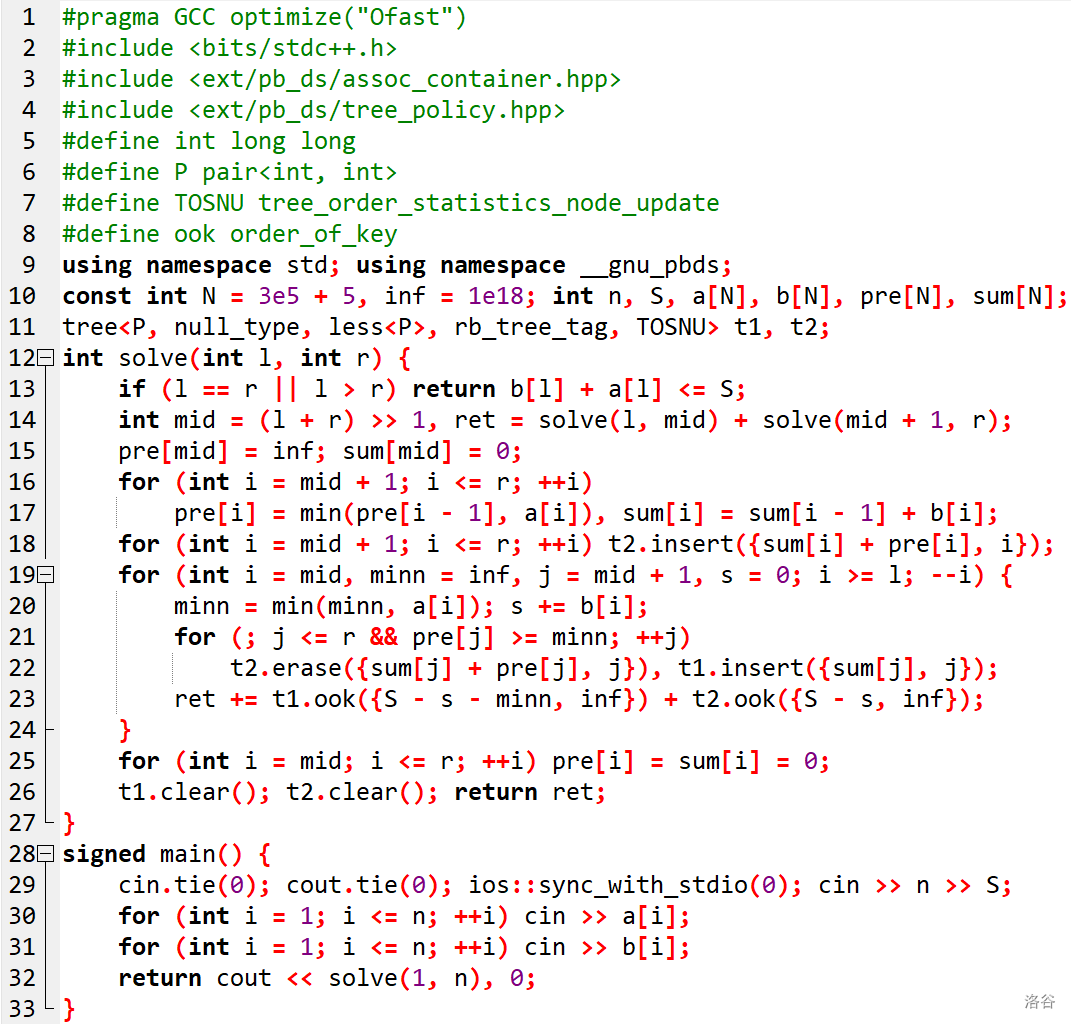
代码还是贴个图吧，让大家感受一下 \(33\) 行 \(1.33\text{KB}\) 小清新代码。