CF1666L Labyrinth

题目传送门

• 给出 \(n\) 个点 \(m\) 条边的有向图，以及一个起点 \(s\)。问是否能找到两条从 \(s\) 出发的不同的路径，满足：

  • 两条路径在同一个点结束。

  • 两条路径除起点、终点外不相交。

  • 每一条路径不经过重复的点。

  称两条路径是不同的，当且仅当它们经过的点数不同，或存在 \(i\) 使得第一条路径的第 \(i\) 个点与第二条路径的第 \(i\) 个点不同。有解时输出方案。

• \(n,m\le 2\times 10^5\)。

先考虑什么时候一定无解，显然 \(s\) 的出度小于 \(2\)。

否则，两条路径一定是从 \(s\) 的两个后继出发，到达某个相同的点，如图：

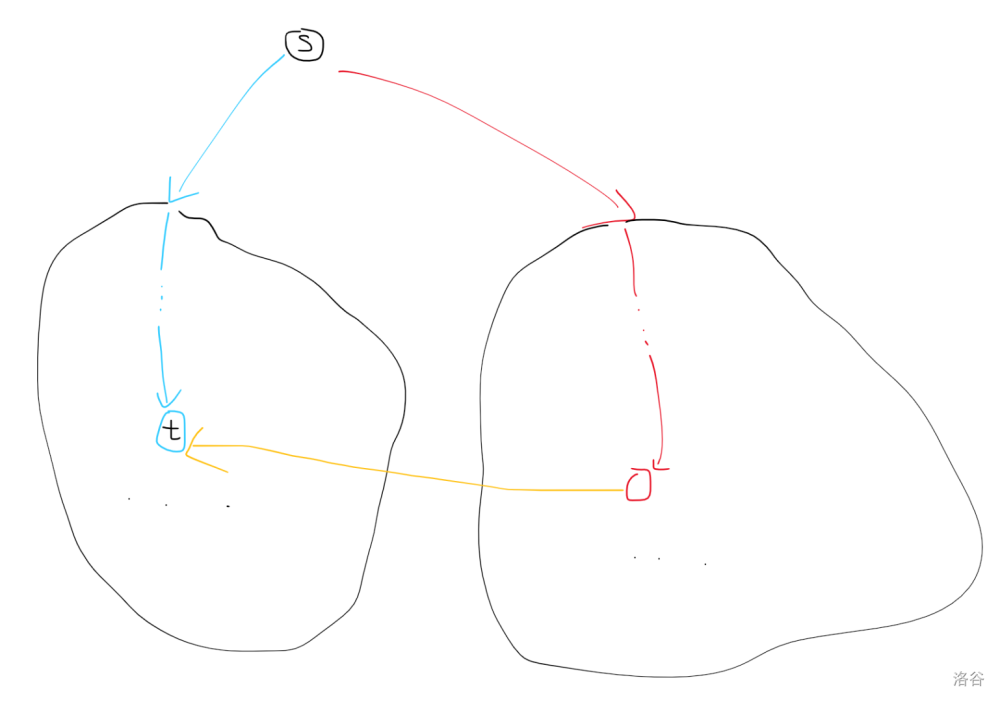
进一步思考，这个形态即为图的一棵搜索树，而若要满足条件，则说明必须存在一条横跨两个后继子树的横叉边。所以先以 \(s\) 为根找出一棵搜索树，然后记录每个点 \(u\) 的父亲 \(fa_u\)。

我们对每个后继的子树用一种独一无二的颜色染色，若遍历当前点 \(u\) 边集的过程中发现与自己颜色不同的点（记为 \(v\)），则说明存在一条这样的横叉边，所求路径即为 \(s\rightsquigarrow v\) 和 \(s\rightsquigarrow u \rightarrow v\)，记录一下这两个点即可。不要像某个人一样忘记了 \(\boldsymbol{s}\) 到后继的边也可以成为横叉边。若不存在这样的 \(u,v\) 则无解。然后你发现这样包含了 \(s\) 的出度小于 \(2\) 的情况。

输出方案的时候，先递归输出自己父亲的路径，再输出自己。第二条路径不要忘记输出点 \(\boldsymbol{v}\)，因为横叉边的结尾是 \(v\)。

时间、空间复杂度均为 \(\mathcal{O}(n+m)\)。

评测记录

#include <bits/stdc++.h>
using namespace std; const int N = 2e5 + 5;
int n, m, s, col[N], cnt, fa[N], p1, p2, tot; vector<int> g[N]; bool op, vis[N];
template<class T> void read(T &x) {
    x = 0; T f = 1; char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -1;
    for (; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + c - 48; x *= f;
}
template<class T> void write(T x) {
    if (x > 9) write(x / 10); putchar(x % 10 + 48);
}
template<class T> void print(T x, char ed = '\n') {
    if (x < 0) putchar('-'), x = -x; write(x), putchar(ed);
}
void init(int u) { 
    vis[u] = 1; for (int v : g[u]) if (!vis[v]) fa[v] = u, init(v);
}
void dfs(int u, int c) {
    if (col[u] != -1 && !op) p1 = u, p2 = s, op = 1; col[u] = c; 
    for (int v : g[u]) {
        if (col[v] == c || !col[v]) continue;
        if (col[v] == -1) dfs(v, c); else if (!op) p1 = v, p2 = u, op = 1; 
    }
}
void find(int u) { 
    if (u != s) ++tot, find(fa[u]); else print(tot); print(u, ' '); 
}
signed main() {
    read(n), read(m), read(s); memset(col, -1, sizeof col);
    for (int i = 1, u, v; i <= m; ++i) read(u), read(v), g[u].emplace_back(v);
    col[s] = 0; init(s); for (int v : g[s]) dfs(v, ++cnt);
    if (!p1 || !p2) return puts("Impossible"), 0; puts("Possible");
    tot = 1, find(p1); puts(""); tot = 2, find(p2), print(p1);
    return 0;
}