ARC165B Sliding Window Sort 2

AT

洛谷

• 给出长度为 \(N\) 的整数排列 \(P_1\sim P_N\)，必须选择一个长度为 \(K\) 的区间，将区间内的数升序排序。求最后可以得到的最大字典序。

• \(K\le N\le 2\times 10^5\)。

我们发现，进行一次排序后排列的字典序不增。若排列中存在长度不低于 \(K\) 的上升子序列，则答案为原排列。

否则，我们肯定希望一段最长的前缀字典序不变，然后剩下的部分字典序变小。这么看似乎就是选择 \([N-K+1,N]\) 这个区间排序，保证了最长的前缀 \(P_1\sim P_{N-K}\) 不变。

实则不然，选择其它的区间排序也可以使得这段前缀的字典序不变，如这组数据：

5 3
5 1 4 3 2

我们若选择 \(P_3\sim P_5\) 这个区间，则得到排列为 \(\{5,1,2,3,4\}\)，而若选择 \(P_2\sim P_4\) 这个区间，得到的排列为 \(\{5,1,3,4,2\}\)，更优。

因此还有考虑怎样的左端点 \(l\,(1\le l\le N-K)\) 能够满足这个性质。首先 \(P_l\sim P_{N-K}\) 必须是一个递增的序列，否则排序会将这个区间变成递增序列，字典序变小。这一步从 \(N-K\) 这个位置往左扫即可。

其次，需要满足 \(\min\limits_{i=N-K+1}^{l+K-1}>P_{N-K}\)，不然 \(P_{N-K+1}\sim P_{l+K-1}\) 中的某些数就会被排到 \(N-K\) 这个位置及以前，使得 \(P_1\sim P_{N-K}\) 这个前缀的字典序变小。这一步维护一下以 \(N-K+1\) 为起点的前缀最小值（代码中的 \(pre\) 数组）即可。

假设有若干个位置满足这个条件，我们一定选择最左边的那个，可以来看一张图：

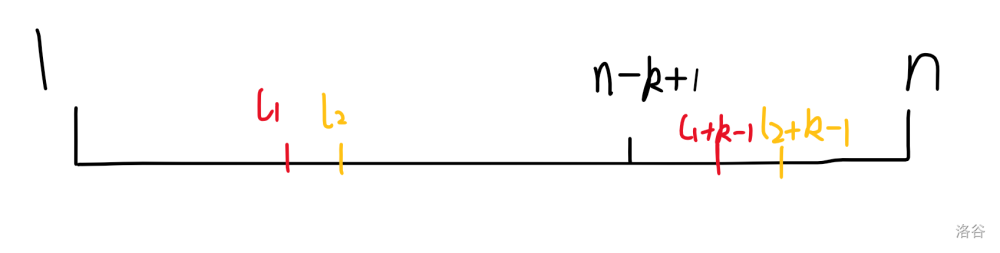
选择 \(l_1\) 或 \(l_2\)，\(P_1\sim P_{N-K}\) 以及 \(P_{l_2+K}\sim P_{N}\) 的顺序都不会发生改变，而对于 \(P_{N-K+1}\sim P_{l_2+k-1}\)，选择 \(l_2\) 会将这个区间进行升序排序，这样一来这个区间的字典序一定是所有重排方式中最小的，显然将 \(P_{N-K+1}\sim P_{l_1+K-1}\) 排序，不动 \(P_{l_1+K}\sim P_{l_2+K-1}\) 也是一种重排方式，选择 \(l_1\) 时其它部分字典序不变，\(P_{N-K+1}\sim P_{l_2+K-1}\) 的字典序不会更小，因此选择 \(l_1\) 更优。

若能找到这样的左端点 \(l\)，就对 \(P_{l}\sim P_{l+K-1}\) 进行排序，否则对 \(P_{N-K+1}\sim P_N\) 进行排序。

时间复杂度为 \(\mathcal{O}(K\log N+N)\)，空间复杂度为 \(\mathcal{O}(N)\)。

评测记录

#include <bits/stdc++.h>
using namespace std; const int N = 2e5 + 5; 
int n, k, a[N], maxn, pos = 1, lg[N], ans, pre[N];
template<class T> void read(T &x) {
    x = 0; T f = 1; char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -1;
    for (; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + c - 48; x *= f;
}
template<class T> void write(T x) {
    if (x > 9) write(x / 10); putchar(x % 10 + 48);
}
template<class T> void print(T x, char ed = '\n') {
    if (x < 0) putchar('-'), x = -x; write(x), putchar(ed);
}
signed main() {
    read(n), read(k); for (int i = 1; i <= n; ++i) read(a[i]), lg[i] = __lg(i);
    for (int i = 1, la, len = 0; i <= n; ++i) {
        if (i == 1 || a[i] > la) ++len; else maxn = max(len, maxn), len = 1;
        la = a[i];
    }
    if (maxn >= k) { for (int i = 1; i <= n; ++i) print(a[i], ' '); return 0; }
    for (int i = n - k, la = N; i >= 1; --i) 
        if (a[i] > la) { pos = i + 1; break; } else la = a[i];
    pre[n - k + 1] = a[ans = n - k + 1];
    for (int i = n - k + 2; i <= n; ++i) pre[i] = min(pre[i - 1], a[i]);
    for (int i = pos; i <= n - k; ++i) 
        if (pre[i + k - 1] > a[n - k]) { ans = i; break; }
    sort(a + ans, a + ans + k); for (int i = 1; i <= n; ++i) print(a[i], ' ');
    return 0;
}