2025深大电协软件部招新个人题解(部分)
2025深大电协软件部招新个人题解(部分)
Miya555忙里偷闲凑出三个小时参与了此次比赛(?),后面题絮絮叨叨的没时间看了,练练手。
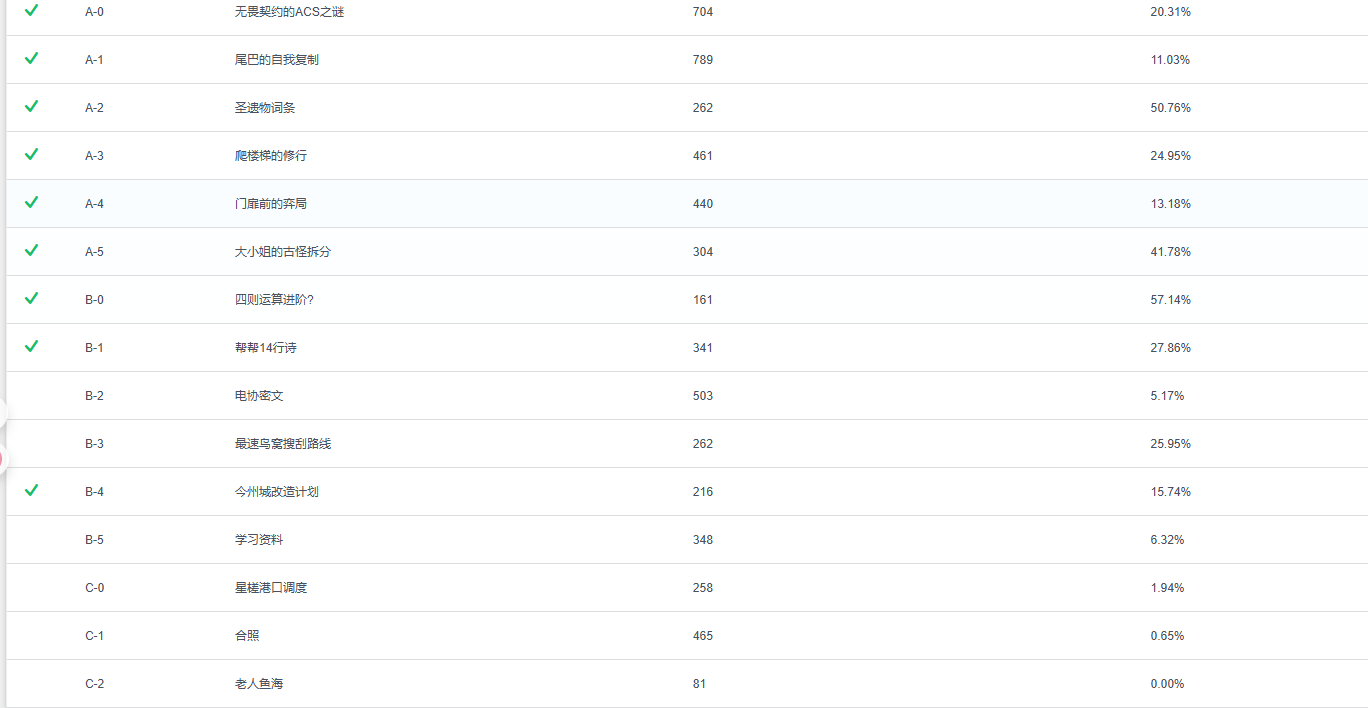
前言:ACM赛制,我的完成度(9/15),题目大部分要么小清新,要么套路,洛谷难度来看红到紫都有,基本以橙黄题为主。最后一题出现了主席树,可爱捏,被我一眼丁真然后跳过了(完全不会)。
不过这份题目放在大一来招新有点超标了吧,我感觉对初学者太不友好了。虽然我不是初学者。

题解部分
A0无畏契约的ACS之谜
签到题,a+b problem四舍五入版
#include<bits/stdc++.h>
using namespace std;
long long n,a,b,c;
long long tmp,tot;
int main()
{
cin>>n;
for(long long i=1;i<=n;i++)
{
cin>>a>>b>>c;
tot+=a*150+b*25+c*50;
if(a>1)
{
tot+=30*(a-1);
}
}
// tmp=0;
cout<<tot/n;
return 0;
}
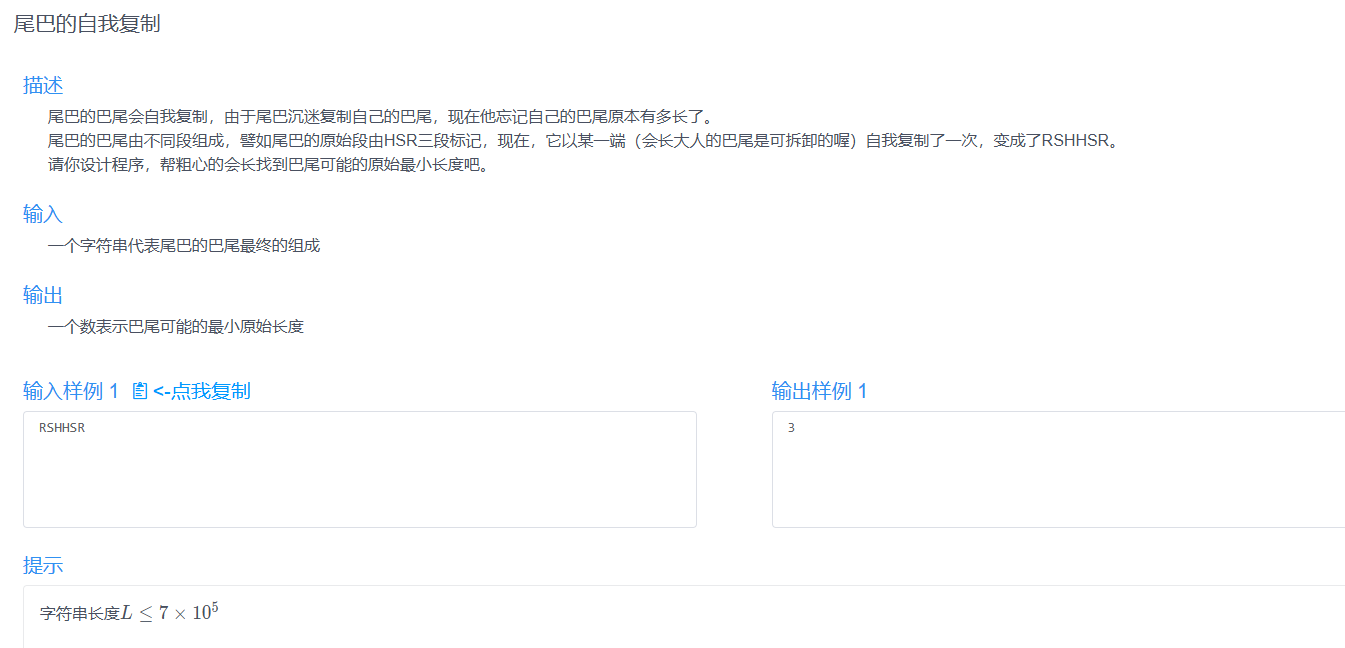
A1尾巴的自我复制
这道题是一个小清新字符串,使用string的小巧思很快解决。
我一开始想成了回文串,手推了一下发现不对,可以直接用substr暴力拆开,两层for循环搞定,一开始还以为会超时,这个数据放的也太松了。
如果我是万恶的出题人,我将严卡TLE
#include<bits/stdc++.h>
using namespace std;
int main() {
string s;
cin >> s;
int n = s.length();
for (int len = 1; len <= n; len++) {
bool valid = true;
for (int i = len; i < n; i += len) {
string cur = s.substr(i, len);
string tmp = s.substr(0, len);
if (cur != tmp) {
string re = tmp;
reverse(re.begin(), re.end());
if (cur != re) {
valid = false;
break;
}
}
}
if (valid) {
cout << len << endl;
return 0;
}
}
// cout << n << endl;
return 0;
}
A2 圣遗物词条

一开始读题感觉很数学,所以直接开始推式子,兜兜转转通过加加减减发现了神秘的状态转移:
设 f[i][j] 为把 i 拆分为 j 个数的方案数,则
这是一个十分重要的表达式,有些难以理解,我画了一下:

确实很有意思,推完之后茅塞顿开,高中的时候教练好像讲过?
后面的代码就很简单了
#include<bits/stdc++.h>
using namespace std;
int f[1010][1010];
//我服了吧,居然是dp,我怎么这么蠢了?
int main() {
int n, m;
cin >> n >> m;
// 初始条件:0拆分为0个数,1种方式
f[0][0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
if (i >= j) {
f[i][j] = f[i - 1][j - 1] + f[i - j][j];
}
}
}
cout << f[n][m] << endl;
return 0;
}
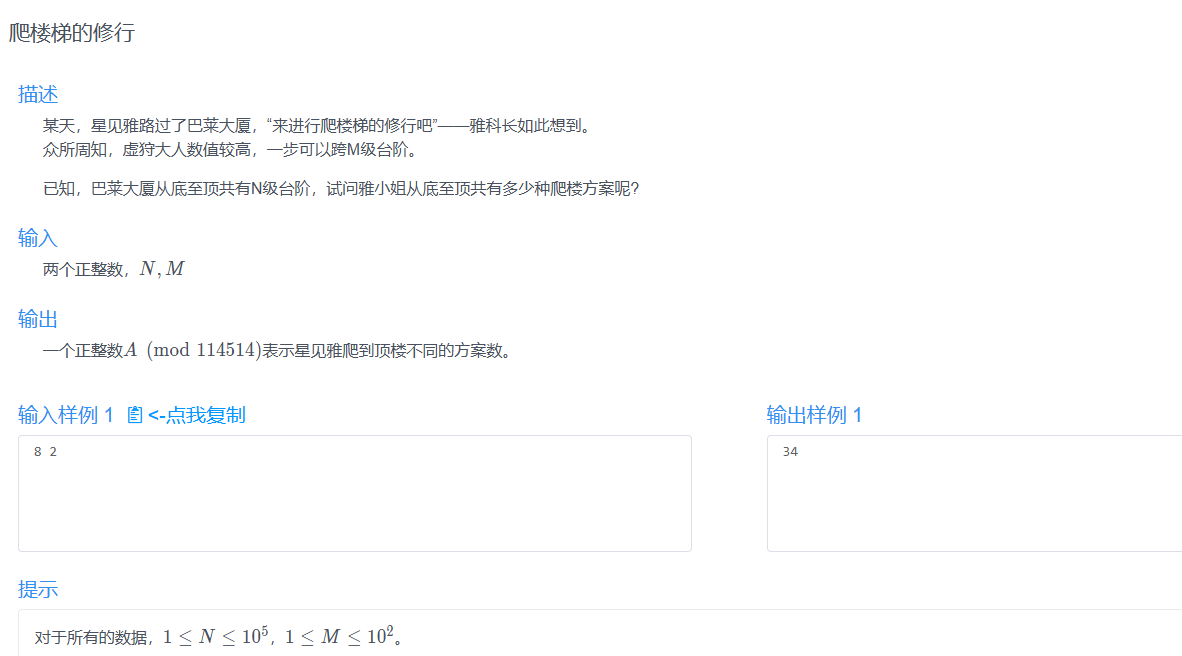
A3 爬楼梯的修行
就是你知道的那个爬楼梯的小变式题。。难度上不到普及-
变处在于 “一步可以跨M级台阶”
在for循环中再做m次加法就可以了
#include<bits/stdc++.h>
using namespace std;
int n,m,f[100010],tmp=1;
const int N=114514;
int main()
{
// f[1]=1,f[2]=2;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
f[i]=tmp;
tmp+=f[i];
tmp%=114514;
}
for(int i=m+1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
f[i]+=f[i-j];
f[i]%=114514;
}
// f[i]=f[i-1]+f[i-2];
}
cout<<f[n];
return 0;
}
不过我当时傻了还弄了个预处理,第一个for循环可以直接使用第二个来代替。代码更少。
A4 门扉前的弈局

刚刚看到这道题以为是过河卒,后面发现又没那么相似。
思路是BFS,一步一步扩展。
先使用两个数组来存储上下前后的位置,用队列和堆来维护坐标
这道题要比较细心!
#include<bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
int n, m, x, y;
int f[500][500]; // 存储到达每个点的最短步数
// 骑士的8个移动方向:(+1,+2), (+1,-2), (-1,+2), (-1,-2), (+2,+1), (+2,-1), (-2,+1), (-2,-1)
int dx[8] = {1, 1, -1, -1, 2, 2, -2, -2};
int dy[8] = {2, -2, 2, -2, 1, -1, 1, -1};
int main() {
cin >> n >> m >> x >> y;
// 初始化:所有点初始为“不可达(INF)”
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
f[i][j] = INF;
}
}
f[x][y] = 0; // 起点步数为0
queue<pair<int, int>> q;
q.push({x, y}); // 起点入队
while (!q.empty()) {
auto [i, j] = q.front();
q.pop();
// 遍历8个方向
for (int k = 0; k < 8; k++) {
int ni = i + dx[k];
int nj = j + dy[k];
// 检查新位置是否在棋盘内,且未被访问过(或能更新为更短步数)
if (ni >= 1 && ni <= n && nj >= 1 && nj <= m && f[ni][nj] == INF) {
f[ni][nj] = f[i][j] + 1; // 步数+1
q.push({ni, nj}); // 新位置入队,继续扩展
}
}
}
// 输出结果:INF改为-1,然后按格式输出
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (f[i][j] == INF) f[i][j] = -1;
cout << f[i][j] << ' ';
}
cout << endl;
}
return 0;
}
A5 大小姐的古怪拆分
拆解最大素数因数,求最小素数因数就好了。点击即送,也是签到题。
#include <bits/stdc++.h>
using namespace std;
int main() {
int a;
cin >> a;
for (int i = 2; i <= a; i++)
if (a % i == 0) {
cout << a / i;
break;
}
return 0;
}
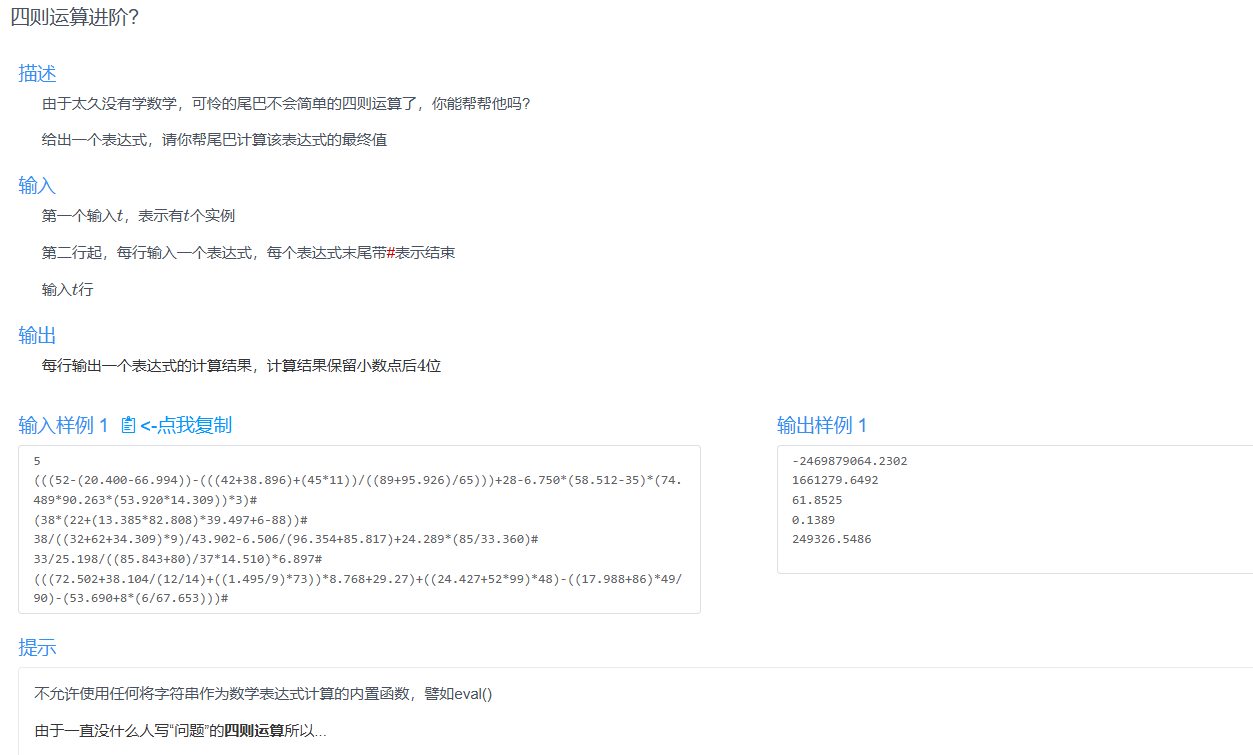
B0 四则运算进阶
做复杂了,想了一个类似于括号匹配的解法,用栈来维护字符串。
绝对不是正解但是也AC了。
#include<bits/stdc++.h>
using namespace std;
//我用栈写的,类似括号匹配的思路。
//怎么写的这么复杂
//为什么通过率这么高??
//输入的读取好像有点问题,还在调试
int priority(char op) {
if (op == '+' || op == '-') return 1;
if (op == '*' || op == '/') return 2;
return 0;
}
void calculate(stack<double>& nums, stack<char>& ops) {
if (nums.size() < 2 || ops.empty()) return;
// 确保栈有足够元素
double b = nums.top(); nums.pop();
double a = nums.top(); nums.pop();
char op = ops.top(); ops.pop();
double res;
switch (op) {
case '+': res = a + b; break;
case '-': res = a - b; break;
case '*': res = a * b; break;
case '/':
if (b == 0) {
res = 0;
} else {
res = a / b;
}
break;
}
nums.push(res);
}
double evaluate(const string& s) {
stack<double> nums;
stack<char> ops;
int i = 0;
int n = s.size();
if (n == 0) return 0; // 空表达式直接返回0
while (i < n) {
if (s[i] == ' ') {
i++;
continue;
}
if (s[i] == '+' || s[i] == '-') {
bool isNegative = (s[i] == '-');
// 负号
if (isNegative && (i == 0 || s[i-1] == '(' || s[i-1] == '+' || s[i-1] == '-' || s[i-1] == '*' || s[i-1] == '/')) {
i++;
double num = 0.0;
bool hasDot = false;
double fraction = 0.1;
// 提取
while (i < n && (isdigit(s[i]) || s[i] == '.')) {
if (s[i] == '.') {
if (hasDot) break; // 避免多个小数点(如1.2.3)
hasDot = true;
i++;
continue;
}
if (!hasDot) {
num = num * 10 + (s[i] - '0');
} else {
num += (s[i] - '0') * fraction;
fraction *= 0.1;
}
i++;
}
nums.push(isNegative ? -num : num);
continue;
}
// 加减
while (!ops.empty() && ops.top() != '(' && priority(ops.top()) >= priority(s[i])) {
calculate(nums, ops);
}
ops.push(s[i]);
i++;
}
// 提取正数或小数
else if (isdigit(s[i]) || s[i] == '.') {
double num = 0.0;
bool hasDot = false;
double fraction = 0.1;
while (i < n && (isdigit(s[i]) || s[i] == '.')) {
if (s[i] == '.') {
if (hasDot) break; // 避免多个小数点
hasDot = true;
i++;
continue;
}
if (!hasDot) {
num = num * 10 + (s[i] - '0');
} else {
num += (s[i] - '0') * fraction;
fraction *= 0.1;
}
i++;
}
nums.push(num);
}
// 左括号直接入栈
else if (s[i] == '(') {
ops.push(s[i]);
i++;
}
// 计算到左括号为止
else if (s[i] == ')') {
// 只计算到左括号
while (!ops.empty() && ops.top() != '(') {
calculate(nums, ops);
}
if (!ops.empty()) { // 确保栈非空再弹左括号
ops.pop();
}
i++;
}
// 乘除
else if (s[i] == '*' || s[i] == '/') {
while (!ops.empty() && ops.top() != '(' && priority(ops.top()) >= priority(s[i])) {
calculate(nums, ops);
}
ops.push(s[i]);
i++;
} else {
// 忽略非法字符
i++;
}
}
// 剩余操作符
while (!ops.empty()) {
calculate(nums, ops);
}
// nums非空
return nums.empty() ? 0 : nums.top();
}
int main() {
int t;
cin >> t;
// 搞了半天,太恶心了
cin.ignore(numeric_limits<streamsize>::max(), '\n');
while (t--) {
string s;
getline(cin, s);
// 去除#
if (!s.empty() && s.back() == '#') {
s.pop_back();
}
// 计算并输出结果
double result = evaluate(s);
printf("%.4lf\n", result);
}
return 0;
}
B1 帮帮14行诗
小清新贪心题
我写这道题的时候边界判断反复出问题,导致WA了好多次。警钟敲烂。
令 m[i] 为i点平衡伞数,f[i] 为i点的方案数,简单贪一下就OK了,自己看吧
则
#include<bits/stdc++.h>
using namespace std;
long long n,m[1000010],f[1000010];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>m[i];
f[i]=0x3f3f3f3f;
}
f[1]=0;
for(int i=1;i<=n;i++)
{
if((i+m[i])<=n)
{
for(int j=i;j<=i+m[i];j++)
{
//if(w[j]!=0)
f[j]=min(f[i]+1,f[j]);
}
//f[i+m[i]]=min(f[i]+1,f[i+m[i]]);
}else{
for(int j=i;j<=n;j++)
{
//if(w[j]!=0)
f[j]=min(f[i]+1,f[j]);
}
// f[n]=min(f[i]+1,f[n]);
}
}
cout<<f[n];
return 0;
}
B4 今州城改造计划
招新就上图论吗,有意思。

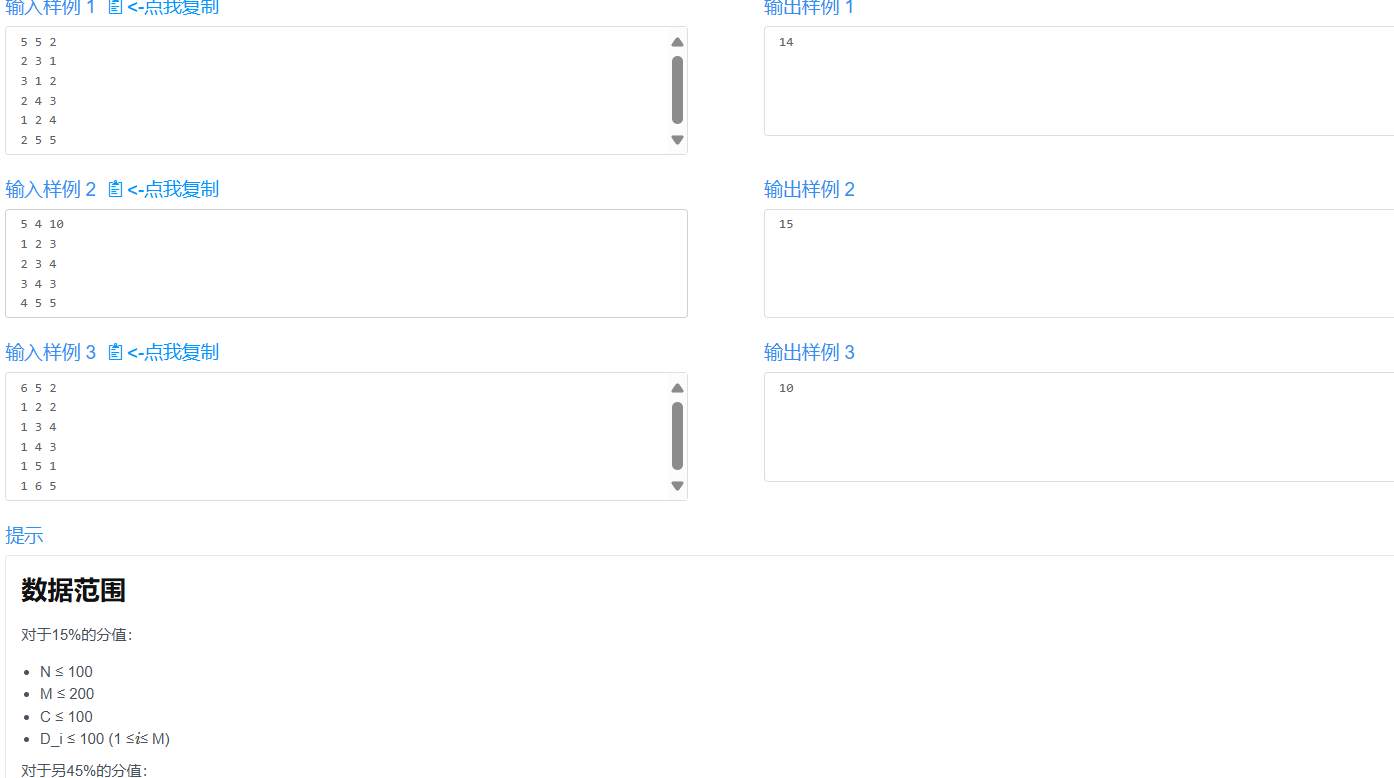
思路是Dijskra,随处优化,我写最简单的Dijskra只能获得50pts。唉。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 1e5 + 5;
const int MAXM = 2e5 + 5;
const ll INF = LLONG_MAX;
struct Edge {
int to, w, next;
} edges[MAXM * 2];
int head[MAXN], idx = 0;
ll dist[MAXN];
int N, M, C;
vector<pair<ll, int>> edge_info;
vector<ll> prefix_sum;
void add_edge(int u, int v, int w) {
edges[idx].to = v;
edges[idx].w = w;
edges[idx].next = head[u];
head[u] = idx++;
edges[idx].to = u;
edges[idx].w = w;
edges[idx].next = head[v];
head[v] = idx++;
}
void dijkstra() {
priority_queue<pair<ll, int>, vector<pair<ll, int>>, greater<>> pq;
fill(dist, dist + MAXN, INF);
dist[1] = 0;
pq.emplace(0, 1);
while (!pq.empty()) {
auto [d, u] = pq.top();
pq.pop();
if (d > dist[u]) continue;
for (int i = head[u]; i != -1; i = edges[i].next) {
int v = edges[i].to;
int w = edges[i].w;
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
pq.emplace(dist[v], v);
}
}
}
}
int main() {
//加速加速加速加速
ios::sync_with_stdio(false);
cin.tie(nullptr);
fill(head, head + MAXN, -1);
cin >> N >> M >> C;
for (int i = 0; i < M; ++i) {
int A, B, D;
cin >> A >> B >> D;
add_edge(A, B, D);
}
dijkstra();
edge_info.reserve(M);
for (int i = 0; i < idx; i += 2) {
int A = edges[i].to;
int B = edges[i ^ 1].to;
int D = edges[i].w;
ll max_d = max(dist[A], dist[B]);
edge_info.emplace_back(max_d, D);
}
sort(edge_info.begin(), edge_info.end());
prefix_sum.resize(M + 1, 0);
for (int i = 0; i < M; ++i) {
prefix_sum[i + 1] = prefix_sum[i] + edge_info[i].second;
}
vector<ll> dists;
for (int i = 1; i <= N; ++i) {
dists.push_back(dist[i]);
}
sort(dists.begin(), dists.end());
dists.erase(unique(dists.begin(), dists.end()), dists.end());
ll min_total = LLONG_MAX;
for (ll X : dists) {
auto it = upper_bound(edge_info.begin(), edge_info.end(), make_pair(X, INT_MAX));
int cnt = edge_info.end() - it;
ll repair = prefix_sum[M] - prefix_sum[M - cnt];
ll total = C * X + repair;
if (total < min_total) {
min_total = total;
}
}
cout << min_total << endl;
return 0;
}
本人能力受限只能写这么多了,剩下的题没写出来qwq
深大还是有很多大佬在的,膜拜。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号