[8]-代码随想录算法训练营-day8-KMP算法

代码随想录训练营-KMP算法学习

1.基础概念

1. 前缀

   • 包含首字母，不包含尾字母的所有子串

2. 后缀

   • 包含尾字母，不包含首字母的所有子串

3. 最长相等前后缀

   • 罗列模式串中所有字符串的前后缀
   • 确定最长相等的前后缀

4. 如何找前后缀：

   • 模式串为aabaaf
   • 则其前缀有：a、aa、aab 、aaba、 aabaa
   • 则其后缀有：f、 af 、aaf、 baaf 、 abaaf

5. 如何找最长相等前后缀

   • 模式串为aabaaf
   • a前缀有：a；无后缀，相等前后缀个数为0
   • aa前缀有：a；后缀有：a，相等前后缀个数为1
   • aab前缀有：a、aa；后缀有：b、ab，个数为0
   • aaba前缀有：a、aa、aab；后缀有：a、ba、aba，个数为1
   • aabaa前缀有：a 、aa、 aab 、aaba；后缀有：a、 aa 、baa、 abaa，个数为2
   • aabaaf前缀有：a、 aa、 aab 、aabaa；后缀有：f 、af 、aaf、 baaf 、abaaf，个数为0
   • 因此，改模式串最长相等前后缀个数为2

6. 什么是前缀表

   • 模式串为aabaaf

   • 从首字母开始，向尾字母移动的过程中，每个子串的相等前后缀个数，如下表：

     a	a	b	a	a	f
     0	1	0	1	2	0

   • 其实就是将5.如何找最长相等前后缀的结果对应到表中

   • 得到的表就是前缀表

2.KMP算法基本工作原理

1. 思想

   • 文本串指针不进行回溯，只朝一个方向移动
   • 模式串进行回溯，回溯距离由前缀表决定
   • 回溯表记录了与后缀相等的前缀末尾的位置
   • 回溯后重新匹配，若匹配失败则模式串继续回溯

2. 图解KMP工作算法
   

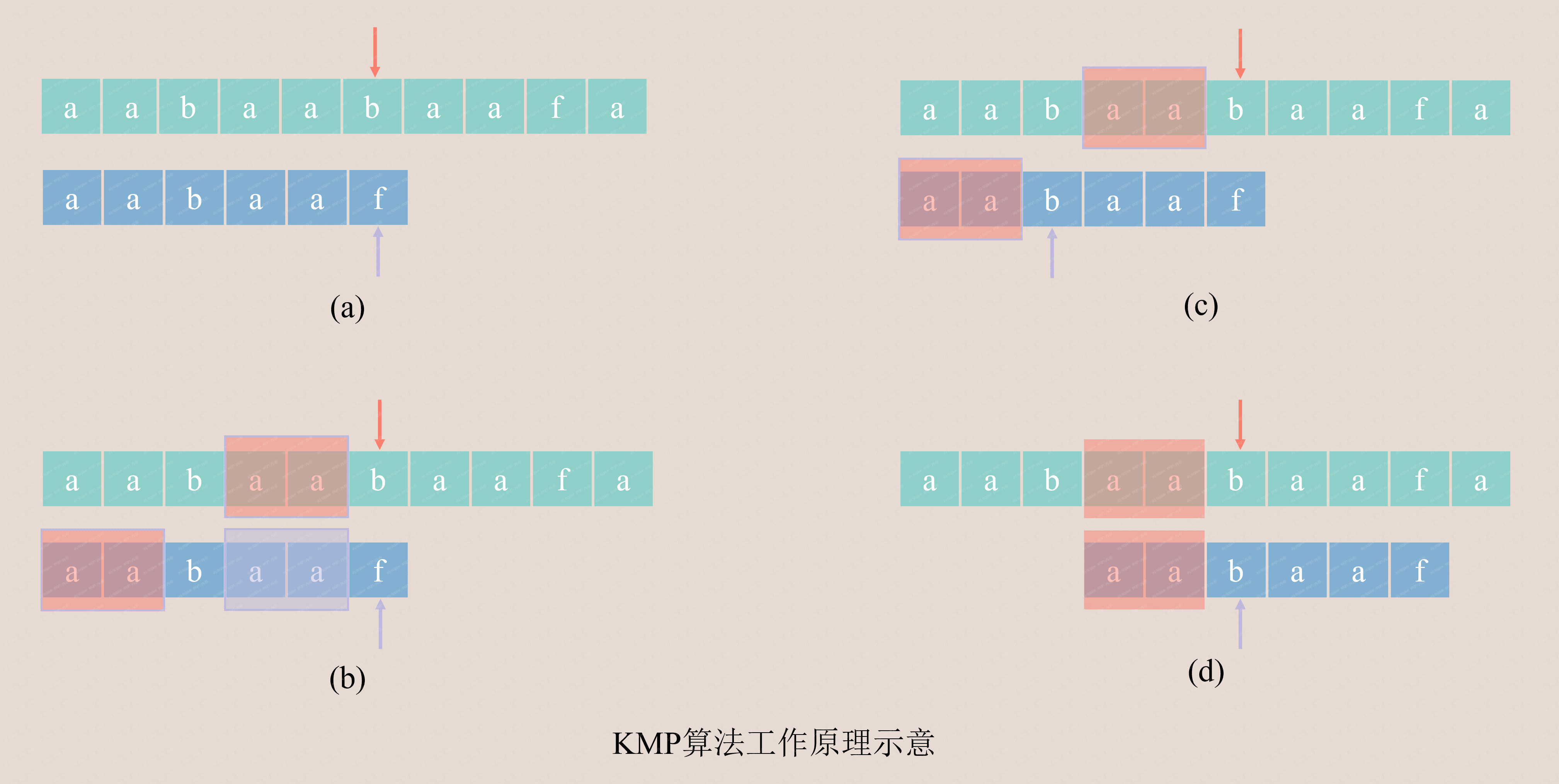
3. 关于KMP算法工作原理示意图的解释

   • 第一步：文本串和模式串开始逐一匹配，当文本串指针行至图a红色指针部分，模式串指针行至图a紫色指针部分，发现不匹配。
   • 第二步：此时发现两指针后面的字符串aabaa存在最长相等前后缀。在图b的模式串中用红色块标注前缀，紫色块标注后缀。
   • 第三步：由于前后缀相等，因此相等部分不需要继续进行匹配，用前缀替代后缀，模式串指针进行回溯，如图c所示。
   • 第四步：模式串指针进行回溯后，文本串和模式串开始进行逐一匹配。

4. 关于模式串的回溯

   • 根据记录的前缀表，即可完成回溯
   • 如果文本串第一次回溯后匹配仍旧失败，则继续执行回溯操作
   • 直至回溯到模式串首字母，然后再逐一进行匹配。
   • 如果回溯到首字母后，仍然匹配失败，则文本串指针执行+1操作，继续匹配。

5. 感悟|收获|心得

   • KMP算法核心思想：文本串指针走向一致，匹配失败后，模式串的后缀由前缀替代进行回溯，仅对模式串相等前缀的后一个字符是否一致即可。
   • 关于next数组的求法：实质是记录其相等前缀的末尾位置，以便于模式串进行匹配时回溯指针。

3.前缀表next数组理论

1. 关于next数组

   • 也叫下一步数组，在KMP算法文本串进行匹配过程中，若出现不一致，则根据next数组确定模式串下一步匹配的地点
   • 换而言之，next数组用于指导文本串下一步与模式串的那一个字符进行比较

2. next数组三种表示方式

   • 前缀表直接表示法：直接用前缀表表示，不做其他操作
   • 前缀右移表示法：将前缀表整体右移动一位，然后空出的首字母用-1表示
   • 前缀减1表示法：求出前缀后，给值进行减1操作

3. 模式串aabaaf用next方式表示的三种方式

   next数组表示方式	a	a	b	a	a	f
   直接表示法	0	1	0	1	2	0
   右移表示法	-1	0	1	0	1	2
   减1表示法	-1	0	-1	0	1	-1

4. next数组求解思路---直接表示法

   • next数组求解即是求解前缀表的过程
   • 用i表示后缀末尾，j表示前缀末尾
   • 初始化i = 1，j = 0
   • 采用直接表示法，用next[i]来记录模式串[0, i]位置的最长相等前后缀长度，则next[0] = 0
   • 当模式串t[i] = t[j]时，即前后缀一致，则next[i] = j + 1，然后j++，i++，前后缀末尾统一后移一位
   • 当模式串t[i] != t[j]时，即前后缀不一致，则j需要向前回溯，则j = next[j - 1]，需要注意保证j-1 >= 0，如果到首字母j = 0后仍不相等，则next[i]= j = 0，且仅进行i++操作

5. next数组求解思路---减1表示法

   • 初始化i = 1，j = -1
   • 右移表示法，next[0] = -1
   • 当模式串t[i] = t[j + 1]时，即前后缀一致，则next[i] = j + 1，然后j++，i++
   • 当模式串t[i] != t[j + 1]时，即前后缀不一致时，则j需要进行回溯，即j = next[j]，注意保证j >= 0。若至首字母j = -1后仍不相等，则next[i] = j = -1，仅进行i++操作

6. next数组求解难点---前缀j回溯操作理解

   • 以笔者目前的理解程度，其实这种回溯过程，仍旧是后缀用前缀替代的过程
   • 将模式串i所走的路径视为模式串中的文本串，即将[0, i]视为文本串
   • 将模式串j所走的路径视为模式串中的模式串，即将[0, j]视为模式串
   • 当j = -1; t[i] != t[j + 1]时，即出现不匹配情况时，则需要把模式串的指针j移动到相等前缀的末尾位置

7. 心得|收获

   • 若carl哥的视频看不懂，可以去天勤考研KMP算法易懂版
   • KMP原理弄明白了，其实很简单，代码写起来也方便。