口胡数论

最大公约数

性质

\[gcd(a,b)=gcd(b,a\%b) \]

\[gcd(a,b)=gcd(a-b,b) \]

\[gcd(a⋅c,b⋅c)=c⋅gcd(a,b) \]

求法

__gcd(a,b)或运用性质一模拟。

ExGCD

求解如 $ax+by=gcd(a,b)$ 一类的不定方程。

裴蜀定理

对于任意非零整数 $a,b，ax+by=c$ 有整数解当且仅当 $c∣gcd(a,b)$。

不定方程求解

由 $gcd(a,b)=gcd(b,a\%b)$ 得：

\[ax+by=bx'+(a\%b)y' \]

\[=bx'+(a-b\lfloor \frac{a}{b}\rfloor)y' \]

\[=ay'+b(x'-y'\lfloor \frac{a}{b} \rfloor) \]

转移到最后，发现 $b=0$,所以 $ax=gcd(a,b)=a,x=1$ 。

把 $x=1,y=0$ 这一组特殊解（因为 $y$ 不一定要选0）转移回去。

递归式为 $x=y',y=x'-y'\lfloor \frac{a}{b} \rfloor$。这样就可以得到一组特殊解了。

void exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1,y=0;//一组特殊解
		return; 
	}
	exgcd(b,a%b,x,y);
	ll ls=x;
	x=y,y=ls-y*(a/b);
}

那有时候有一组解肯定不够，为了推广到所有解，我们有以下的式子：

令 $d=gcd(a,b)$:

\[x=x_0+\frac{b}{d}*k \]

\[y=y_0-\frac{a}{d}*k \]

代入原方程 $( ax + by = d )$ 验证。

代入后：

\[a \left( x_0 + \frac{b}{d} k \right) + b \left( y_0 - \frac{a}{d} k \right) = a x_0 + \frac{a b}{d} k + b y_0 - \frac{a b}{d} k \]

\[= a x_0 + b y_0 + \left( \frac{ab}{d} - \frac{ab}{d} \right) k \]

\[= a x_0 + b y_0 = d \]

所以得证。

欧拉函数

定义

$φ(n)$ 意为 $[1,n]$ 中与$n$ 互质的数的数量。
因式分解，$n=p_1^{c_1},p_2^{c_2},p_3^{c_3}...p_m^{c_m}$,则

\[φ(n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})(1-\frac{1}{p_3})...(1-\frac{1}{p_m}) \]

可以化一下式子：

\[\varphi(n) = n \cdot \frac{p_1 - 1}{p_1} \cdot \frac{p_2 - 1}{p_2} \cdots \frac{p_m - 1}{p_m} \]

这就是一个 $O(\sqrt n)$ 求单个欧拉函数的方法。

ll phi(ll x){
	ll res=x;
	for(int i=2;i*i<=x;i++){
		if(x%i==0){
			res=res/i*(i-1);
			while(1){
				if(x%i!=0){
					break;
				}
				x/=i;
			}
		}
	}
	if(x!=1){
		res=res/x*(x-1);
	}
	return res;
}

性质

若 $p$ 为质数，则 $φ(p)=p-1$。
若 $a,b$ 互质，则$φ(ab)=φ(a)*φ(b)$，所以欧拉函数是积性函数。
$\sum_{d|n}φ(d)=n$。
对于 $n>1$，$[1,n]$ 中与 $n$ 互质的数的和为 $\frac{1}{2}n*φ(n)$。
若 $n=p^k$，并且 $p$ 为质数，则 $φ(n)=p^k-p^{k-1}$。

筛法

运用第二条性质，可以 $O(n)$ 处理 $[1,n]$ 之间的欧拉函数值。

欧拉定理

若 $ a $ 与 $ m $ 互素（即 $ \gcd(a, m) = 1 $），则：

\[a^{\varphi(m)} \equiv 1 \pmod{m} \]

由此可得：

\[a^b \equiv a^{b \bmod \varphi(m)} \pmod{m} \quad \text{当 } b \geq \varphi(m) \]

但这个结论仅在 $ \gcd(a, m) = 1 $ 时成立。

扩展欧拉定理

扩展欧拉定理放宽了互素条件，适用于任意整数 $ a $ 和 $ m $，只要 $ a > 0, m > 0 $。

定理内容：

对于任意整数 $ a, m $ 满足 $ a > 0, m > 0 $，有：

\[a^b \equiv \begin{cases} a^{b \bmod \varphi(m)} & \text{若 } b < \varphi(m) \\ a^{b \bmod \varphi(m) + \varphi(m)} & \text{若 } b \geq \varphi(m) \end{cases} \pmod{m} \]

//a^b%m
ll po(ll x,ll y){
    ll ans=1;
    while(y){
        if(y&1){
            ans=ans*x%m;
        }
        x=x*x%m;
        y/=2;
    }
    return ans;
}
ll phi(ll x){
    ll ls=x;
    for(int i=2;i*i<=x;i++){
        if(x%i==0){
            ls=ls/i*(i-1);
            while(1){
                if(x%i!=0){
                    break;
                }
                x/=i;
            }
        }
    }
    if(x!=1){
        ls=ls/x*(x-1);
    }
    return ls;
}
ll read(){
	ll x=0;
	bool re=0;
	char c=getchar();
	while(c<'0'||c>'9') c=getchar();
	while(c>='0'&&c<='9'){
		x=(x<<3)+(x<<1)+(c-'0');
		if(x>=ls){
			x%=ls;
			re=1;
		}
		c=getchar();
	}
	if(re==1)
		return (x+ls);
	else{
		return x;
    }
}
int main(){
    cin>>a>>m;
    ls=phi(m);
    b=read();
    cout<<po(a,b);
}

应用：幂塔取模

扩展欧拉定理常用于计算形如：

\[a^{a^{a^{\cdots}}} \mod m \]

（共 $ n $ 层）

方法：递归降模

定义函数 $ f(a, n, m) = a^{a{\cdots}} \mod m $（$ n $ 层）

利用扩展欧拉定理，递归地将模数变为 $ \varphi(m), \varphi(\varphi(m)), \ldots $，直到模数为 1。

递归步骤：

若 $ m = 1 $，返回 0
若 $ n = 1 $，返回 $ a \mod m $
计算 $ \varphi = \varphi(m) $
计算 $ t = f(a, n-1, \varphi) $
若 $ t < \varphi $，则结果为 $ a^t \mod m $
否则，结果为 $ a^{t + \varphi} \mod m $

莫比乌斯函数

定义

莫比乌斯函数的符号为 $μ$，通俗的来讲:

如果 $n=1$ ,$μ(n)=1$。
如果 $n$ 为质数，$μ(n)=-1$。
当 $n$ 的因数大于两个时，$μ(n)=(-1)^d$。其中 $d$ 为 $n$ 的因数个数。

如果前三条都不满足，$μ(n)=0$。

性质

莫比乌斯函数在n=1时 $\sum_{d|n}μ(d)$ 为1，其他时候为0。
若 $a,b$ 互质，则$μ(ab)=μ(a)*μ(b)$，所以莫比乌斯函数是积性函数。
对于任意整数 $n$，$\sum_{d|n}\frac{μ(d)}{d}=\frac{φ(n)}{n}$。

筛法

根据寄性函数性质，我们可以 $O(n)$ 筛出所有莫比乌斯函数值。


bool is_not_prime[1000000],primes[1000000],prime_num;
ll mu[1000000];//莫比乌斯函数值 
void find_mbws(){//阿里乌...呸，莫比乌斯 
	is_not_prime[0]=in_not_prime[1]=1;
	mu[1]=1;
	for(int i=2;i<=MAXNUM;i++){
		if(!is_not_prime[i]){
			primes[++prime_sum]=i;
			mu[i]=-1;//质数，-1 
		} 
		for(int j=1;j<=prime_sum,primes[j]*i<=MAXNUM;j++){
			is_not_prime[primes[j]*i]=1;
			if(!(i%primes[j])){//确保有平方因子的数的莫比乌斯函数值为0
				break;
			}
			else{
				mu[primes[j]*i]=-mu[i];
			}
		}
	} 
}

整除分块（技巧）

求：

\[\sum^{n}_{i=1}\lfloor \frac{n}{i}\rfloor \]

不难发现，$\lfloor \frac{n}{i}\rfloor$ 会有很多重复的。

可以分析出，每一个值相同的块，右端点为$n/(n/i)$。

这样就可以 $O(\sqrt n)$ 解决此问题，在很多数论模块都能用到。

for(int l=1,r;l<=n;l=r+1){
    r=n/(n/l);
    ans+=(r-l+1)*(n/l);
}

卢卡斯定理

卢卡斯定理是组合数学中一个非常重要的定理，它用于计算大组合数取模的值，特别是当模数是一个不太大的质数时，它能将大问题分解为多个小问题，极大地简化计算。

定理内容

设 $p$ 是一个质数，将非负整数 $m$ 和 $n$ 用 $p$ 进制表示：

\[m = m_k p^k + m_{k-1} p^{k-1} + \cdots + m_1 p + m_0 \]

\[n = n_k p^k + n_{k-1} p^{k-1} + \cdots + n_1 p + n_0 \]

（如果位数不同，可以在前面补零使其位数一致）

那么有：

\[\binom{m}{n} \equiv \prod_{i=0}^{k} \binom{m_i}{n_i} \pmod{p} \]

其中，$\binom{m}{n}$ 是组合数。并且规定：如果 $n_i > m_i$，则 $\binom{m_i}{n_i} = 0$。

证明略。记住结论就好。

//卢卡斯定理
ll c(ll n,ll m){
    if(m>n){
        return 0;
    }
    return ((jc[n]*po(jc[n-m],mod-2))%mod*po(jc[m],mod-2))%mod;
}
ll lucas(ll n,ll m){
    if(m==0){
        return 1;
    }
    return c(n%mod,m%mod)*lucas(n/mod,m/mod)%mod;
}
int main(){
    ll t;
    cin>>t;
    while(t--){
        ll n,m;
        cin>>n>>m>>mod;
        jc[0]=1;
        for(int i=1;i<=100005;i++){
            jc[i]=(jc[i-1]*i)%mod;
        }
        //m>=n
        cout<<lucas(m,n)<<"\n";
    }
}

卡特兰数

定义

$C(n)$ 表示从原点出发，每次向 $x$ 或$y$ 轴正方向移动1单位，到达点 $(n,n)$，且在移动过程中不越过第一象限平分线的移动方案数。

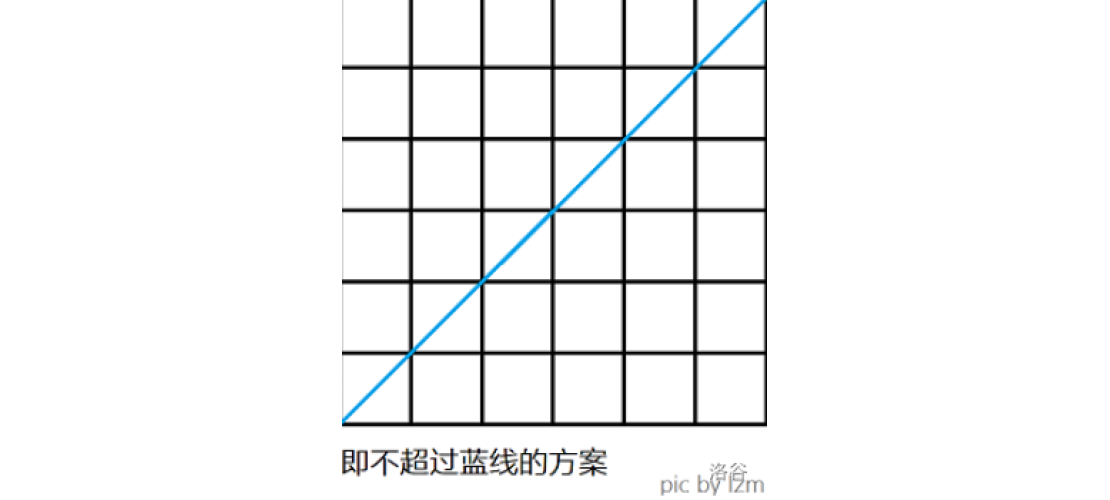
推导

\[C(n) = \binom{2n}{n} - \binom{2n}{n+1} \]

\[C(i) = \frac{(4i-2)}{i+1} C(i-1), \quad C(0) = 1 \]

for(int i=1;i<=n;i++){
    C[i]=(C[i-1]*(4*i-2))%mod;
    C[i]=C[i]*po(i+1,mod-2)%mod;
}

卡特兰数前 $6$ 项：$1, 1, 2, 5, 14, 42$，可以背一下。

推广

当然，我们也可以从 $n*n$ 推广到 $n*m$。

显然，我们要从 $(0,0)$ 走到 $(n,m)$，而且不能走到对角线上。

我们看图：

显然，我们对称了之后，发现所有不和法的方案都可以和从 $(0,0)$ 到 $(n-1,m+1)$ 一一对应，也就是不合法的方案为：

\[\binom{n + m}{n - 1} \]

总方案为：

\[\binom{n + m}{n} - \binom{n + m}{n - 1} \]

posted @ 2025-08-07 15:04 MistyPost 阅读(14) 评论(0) 收藏举报

刷新页面返回顶部

MistyPost

不知道写什么好。凯迪拉克快签小周！

口胡数论

最大公约数

性质

求法

ExGCD

裴蜀定理

不定方程求解

欧拉函数

定义

性质

筛法

欧拉定理

扩展欧拉定理

定理内容：

应用：幂塔取模

莫比乌斯函数

定义

性质

筛法

整除分块（技巧）

卢卡斯定理

定理内容

卡特兰数

定义

推导

推广

公告

MistyPost

不知道写什么好。 凯迪拉克快签小周！

口胡数论

最大公约数

性质

求法

ExGCD

裴蜀定理

不定方程求解

欧拉函数

定义

性质

筛法

欧拉定理

扩展欧拉定理

定理内容：

应用：幂塔取模

莫比乌斯函数

定义

性质

筛法

整除分块（技巧）

卢卡斯定理

定理内容

卡特兰数

定义

推导

推广

公告

不知道写什么好。凯迪拉克快签小周！