最小表示法总结

P1368 【模板】最小表示法

题目描述

现在要做一个由方块构成的长条工艺品。但是方块现在是乱的，而且由于机器的要求，他们只能做到把这个工艺品最左边的方块放到最右边。

他们想，在仅这一个操作下，最漂亮的工艺品能多漂亮。

两个工艺品美观的比较方法是，从头开始比较，如果第 \(i\) 个位置上方块不一样那么谁的瑕疵度小，那么谁就更漂亮，如果一样那么继续比较第 \(i+1\) 个方块。如果全都一样，那么这两个工艺品就一样漂亮。

输入格式

第一行一个整数 \(n\)，代表方块的数目。

第二行 \(n\) 个整数，每个整数按从左到右的顺序输出方块瑕疵度的值，保证其小于 \(30\)。

输出格式

一行 \(n\) 个整数，代表最美观工艺品从左到右瑕疵度的值。

输入输出样例 #1

输入 #1

10
10 9 8 7 6 5 4 3 2 1

输出 #1

1 10 9 8 7 6 5 4 3 2

我们来举个例子来讲述这个算法的核心思想。

先定义两个指针 \(l\) \(r\)，还有一个位移量 \(k\)。

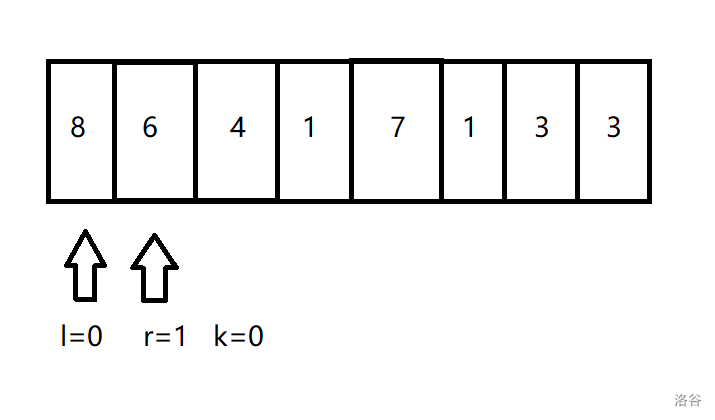
不难看出，此时 \(a_l>a_r\) 所以选 \(r\) 更优，所以左端点加一。

当 \(a_l<a_r\) 时，同理，右端点加一。

但是如果是 \(a_l=a_r\)，那么我们就得让位移量加一，来看看后面的大小关系怎么样。

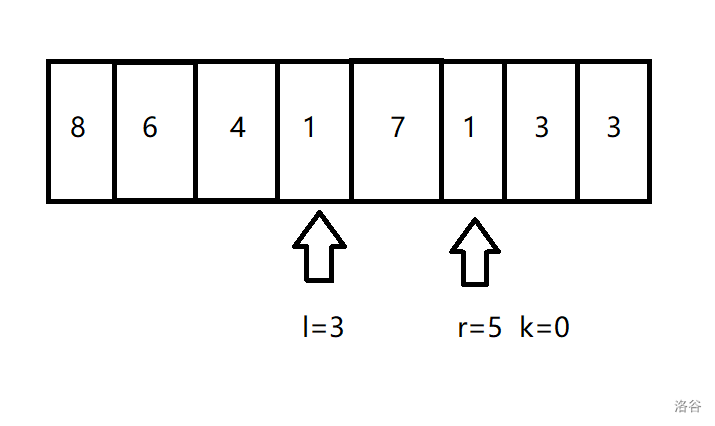
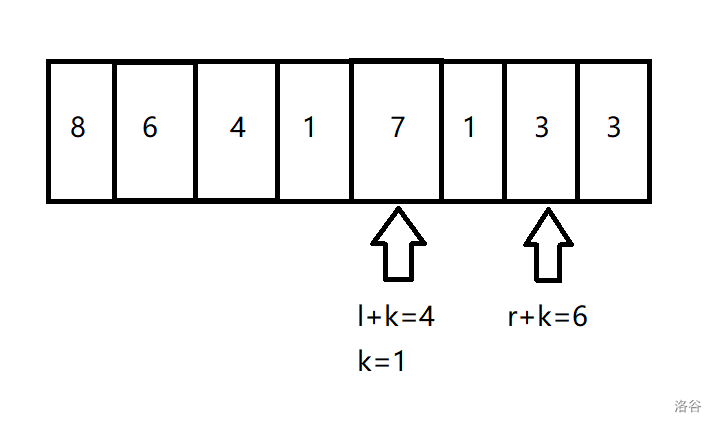
由此可见，选 \(r\) 更优，所以让 \(l=l+k+1\) 继续做即可。

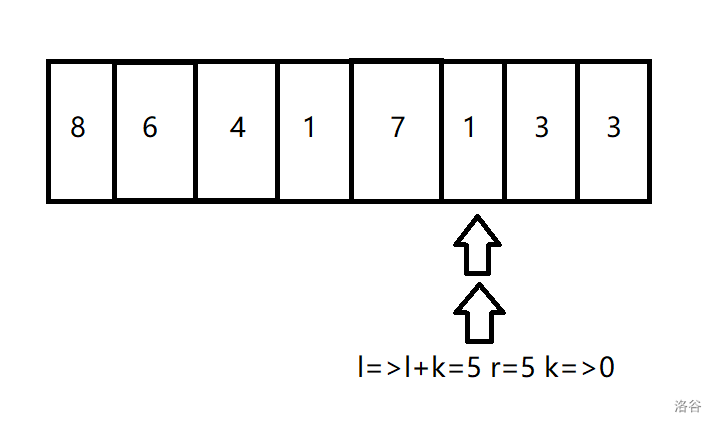
在这里，为了防止 \(l=r\) 导致的无限循环，我们得让 \(r\) 加上一。

这就是核心思想了。

答案是两个指针中的较小值。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll n,l;
ll a[1000000];
ll doo(){
	ll l=0,r=1,k=0;
	while(l<n&&r<n){
		k=0;
		while(a[(l+k)%n]==a[(r+k)%n]&&k<n){
			k++;
		}
		if(k==n){
			return min(l,r);
		}
		if(a[(l+k)%n]>a[(r+k)%n]){
			l=l+k+1;
		}
		else{
			r=r+k+1;
		}
		if(l==r){
			r++;
		}
	}
	return min(l,r);
}
int main(){
	cin>>n;
	for(int i=0;i<n;i++){
		cin>>a[i];
	}
	ll ans=doo();
	for(int i=0;i<n;i++){
		cout<<a[(ans+i)%n]<<" ";
	}
}