题解：P11117 [ROI 2024 Day 2] 交互式通道

题面

---

先特判掉存在 \(1-(0)-1\)，和 \(0-(1)-0\) 的情况，显然在结束时不可能出现这种情况。

然后发现 \(1-(1)-1\)，和 \(0-(0)-0\) 的边在最终将所有楼的开关状态调对后是自然满足的。

所以我们只用考虑 \(1-(0)-0\) 和 \(1-(1)-0\) 这两类边。

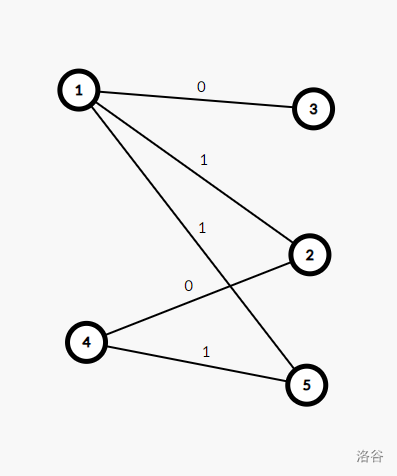
考虑上图，其中左部的楼最终要把灯打开。

对于 \(4-5\) 这样一条 \(1-(1)-0\) 的边，我们可以考虑这样一种策略，先将 4 号楼的灯打开，然后打开并立即关闭 5 号楼的灯。

但是，如果我们先点亮了 4 号楼再点亮 1 号楼，我们会发现处理 \(1-2\) 时会导致 \(4-2\) 这条边不合法。这引导我们按照一定的顺序处理左部点。具体的，对于每一个右部点，所有以边权为 1 连向它的左部点应在以边权为 0 的边连向它的点之前被处理，我们可以建虚点并跑一个拓扑排序求出一个合法的顺序。

最后，考虑一下总操作次数：每个左部点需要操作一次，一条边最多带来两次操作，总计 \(n+2m\le5\times10^5\)。

---

代码：

#include<bits/stdc++.h>
#define int long long
#define lowbit(x) (x&-x)
#define mp(a,b) make_pair(a,b)
using namespace std;
char buf[1000005],*p1,*p2;
#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++)
int read(){
	int x=0,f=0,c=gc();
	while(!isdigit(c))f|=(c=='-'),c=gc();
	while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=gc();
	return f?-x:x;
}
int T,n,m,a[200005],tot,ff[200005];
struct edge{
	int u,v,w;
}e[200005];
struct node{
	int v,w;
};
vector<int>X,Y,g[200005];
vector<int>G[200005];
int topo[200005],in[200005];
bool Topo(){
	queue<int>q;
	for(int i=1;i<=tot;i++)in[i]=0;
	for(int i=1;i<=tot;i++){
		for(int v:G[i])in[v]++;
	}
	for(int i=1;i<=tot;i++)if(!in[i])q.push(i);
	int tt=0;
	while(!q.empty()){
		int tmp=q.front();
		q.pop();
		topo[++tt]=tmp;
		for(int v:G[tmp]){
			in[v]--;
			if(!in[v])q.push(v);
		}
	}
	return tt==tot;
}
vector<pair<int,int> >ans;
signed main()
{
	T=read();
	while(T--){
		n=read(),m=read();
		for(int i=1;i<=n+n;i++)g[i].clear();
		X.clear();
		Y.clear();
		for(int i=1;i<=m;i++)e[i].u=read(),e[i].v=read(),e[i].w=read(),g[e[i].u].push_back(i),g[e[i].v].push_back(i);
		for(int i=1;i<=n;i++)a[i]=read();
		bool f=0;
		for(int i=1;i<=m;i++){
			if(a[e[i].u]==a[e[i].v]&&a[e[i].u]!=e[i].w){
				f=1;
				break;
			}
		}
		if(f){
			puts("NO");
			continue;
		}
		for(int i=1;i<=n+n;i++)G[i].clear();
		tot=n;
		for(int i=1;i<=n;i++){
			if(!a[i]){
				Y.push_back(i);
				vector<int>xx,yy;
				for(int p:g[i]){
					int v=(e[p].u^e[p].v^i);
					if(a[v]){
						if(e[p].w)xx.push_back(v);
						else yy.push_back(v);
					}
				}
				tot++;
				a[tot]=0;
				for(int x:xx)G[x].push_back(tot);
				for(int x:yy)G[tot].push_back(x);
			}
			else X.push_back(i);
		}
		if(!Topo()){
			puts("NO");
			continue;
		}
		ans.clear();
		puts("YES");
		for(int i=1;i<=tot;i++){
			int u=topo[i];
			if(a[u]&&u<=n){
				ans.push_back(mp(u,1));
				for(int v:g[u]){
					int vv=(e[v].u^e[v].v^u);
					if(!a[vv]&&e[v].w){
						ans.push_back(mp(vv,1));
						ans.push_back(mp(vv,0));
					}
				}
			}
		}
		printf("%lld\n",ans.size());
		for(auto x:ans)printf("%lld %lld\n",x.first,x.second);
	}
	return 0;
}