ZR24 Summer A Day4 | Counting
P4099 [HEOI2013] SAO
如果全部都是 \(<\) 的话很好办,那就是外向树拓扑序个数,为 \(\dfrac{n!}{\prod size_u}\)。
现在我们多了内向边,于是需要把他们容斥掉。假设钦定了 \(c\) 条符号为 \(>\) 的边不满足性质(变成了 \(<\) 号的边),那么就有 \((-1)^c\) 的系数。这样子最后会形成一个森林,一颗树的内部有拓扑序要求,树和树之间无要求。合并两颗大小分别为 \(n\) 和 \(m\) 的树的方案数为将排名 \([1,2\dots n]\) 和排名 \([1,2\dots m]\) 整合到排名 \([1,2\dots n+m]\) 的方案数,你只需要在这 \(n+m\) 个位置中选 \(n\) 个位置依次填入原排名为 \(1,2\dots n\) 的数即可,那么就是 \({n+m\choose n}\)。
考虑带着容斥系数进行 dp,每钦定一条边就 \(\times (-1)\)。
由于贡献系数是和子树大小相关的,所以我们要在 dp 的时候记录当前联通块的大小。所有设 \(f_{u,i}\) 表示在 \(u\) 点的时候其所在联通块大小为 \(i\) 的时候的带着容斥系数的方案数之和。根据拓扑序公式,每次遇到一个大小为 \(i\) 的子树都要乘上 \(\dfrac{1}{i}\) 的贡献,这个我们放在最后乘,下面的转移式子中不讨论这一项。
在遇到 \(<\) 的时候,就是 \(\dfrac{n!}{\prod sz_i}\) 和 \(\dfrac{m!}{\prod sz_i}\) 变成 \(\dfrac{(n+m)!}{\prod sz_i}\),我们发现这个变化恰好是 \(\dfrac{(n+m!)}{n!\times m!}={n+m\choose n}\)。
在遇到 \(>\) 的时候,可以选择不钦定那么就是任意顺序,是森林的合并,有系数 \({sz_u+sz_v\choose sz_u}\),或者钦定为 \(<\),和第一个转移系数相同就是多了一个 \(-1\)。
注意每次做完转移之后要 \(f_{u,i}\gets f_{u,i}\times \dfrac{1}{i}\)。
时间复杂度 \(O(n^2)\)。
QOJ8047. DFS Order 4
由于可能多颗树能得到相同的 dfs 序,所以我们可以来考虑有多少种 dfs 序可以还原到一颗合法的树。需要判定序列合法性。
如何判定一个序列合法?我们贪心的把点往一条父链上挂。如果 \(p_i>p_{i-1}\),那么可以挂在这条链末尾 \(p_{i-1}\) 的下方。如果 \(p_i>p_{i-1}\),我们可以在这条链上找到一个最浅的祖先满足 \(p_k<p_i\),我们把 \(p_i\) 挂在 \(p_k\) 的父亲上(这相当于 dfs 的回溯过程),这样子既满足兄弟节点编号递增,也满足了儿子大于父亲。这样子排列就和树一一对应了。
这样子贪心连出来的树等价于以下限制:每个点编号大于父亲,每个点儿子编号单调递增,且小于上一个兄弟的最后一个儿子。
可以发现第 \(2\) 到 \(k\) 个兄弟节点和父亲间的约束没有用,可以通过 \(son_2>son_1>fa\) 来得到。直接删掉就行了,只有在兄弟之间连边。
有一个结论就是一颗外向图的拓扑序个数是 \(\dfrac{n!}{\prod sz_i}\)。但是本题由于有了小于上一个兄弟的最后一个儿子这个限制,导致这不是一颗外向树。
考虑容斥掉这条边,也就是 \([u<v]=1-[u>v]\)。等号右边的两种情况都是一棵树,第一种情况系数是 \(+1\),第二种情况系数是 \(-1\)。
现在需要分析一下新构建的外向树长什么样子。从父子关系角度考虑,有如下三种:一个父亲和它的第一个儿子,相邻兄弟,上一个兄弟的最后一个儿子和这个点。
现在考虑在一层兄弟链上面考虑,其中不止有第二类边,还有第三类边,也就是中间会夹杂着若干个上一个兄弟的一堆儿子。在链上如果走到了下方的节点,根据上述边分类,可以发现这是属于 \(-[u>v]\) 这种边的需要乘上一个 \(-1\) 的系数。
设 \(d_i\) 表示 \(sz=i\) 的子树的贡献,在链上挂子树的时候算贡献。\(f_{i,k}\) 表示 \(sz=i\),在链上深度走到了 \(k\) 的方案数。
首先有 \(f_{i,0}=g_i\)。
合并子树,
往下走,
往上走,
直接在一条链上往上连一个点,
注意一下细节,我们是按照 \(sz\) 从小往大处理,所以有些 \(f_{i,k}\times d_j\) 的 \(d_j\) 在 \(i\) 处还没有被算到,需要在 \(j\) 处再处理一下。
答案就是 \(d_n\)。时间复杂度 \(O(n^3)\)。
AGC020F Arcs on a Circle
环是难做的,所以先断环为链。为了不多算同构的形式,我们可以钦定断开点为最长线段的起点。要求其从 \(0\) 开始,最后覆盖 \([0,C)\) 之内的所有位置。
为什么不随便钦定一条线段呢?其实是为了规避掉较长线段在末尾处饶了一圈又超过了开头的线段(我们钦定的那个),这就会产生一些别的覆盖。但是如果选了最长的线段作为开头,别的线段就算从末尾
环长和线段长都是整数很舒服,但是起点为实数就有一些恶心了。但是我们只关心这些线段是否能连起来,本质上是整数部分相同时,关于小数部分大小的讨论。
于是我们用 \(n!\) 种序列,来描述小数部分的相对大小关系。由于引入了小数部分,原本 \(C\) 个整数坐标,也扩展到了 \(Cn\) 个整数坐标。
然后再状压 dp 一下就行了。
AGC036F Square Constraints
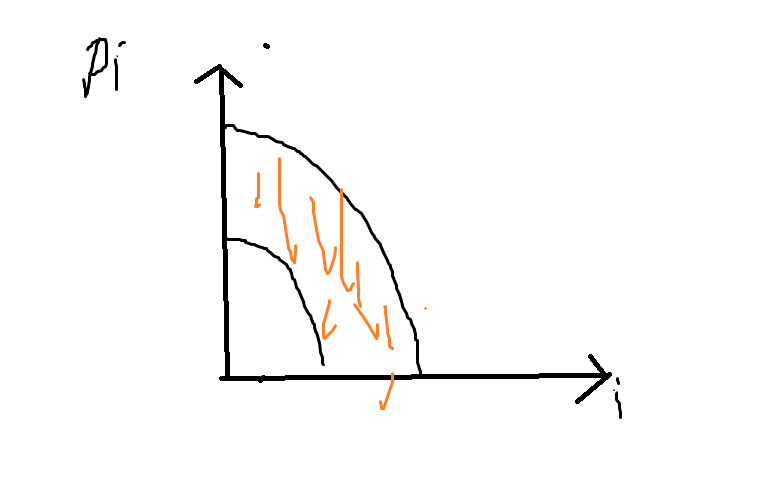
我们画一下 \(P_i-i\) 可选区域的关系图。其实这本质是 \(p_i\in[l_i,r_i]\) 的排列计数。
考虑只有上界怎么做?对于 \(p_i\in[1,r_i]\) 的排列计数,我们可以将 \(r_i\) 排序,然后乘法原理那么总方案数是 \(\prod (r’_i-i+1)\)。
那么如何处理下界?方法是容斥!
某计数题
对于每个 \(x,y\),求有多少个长度为 \(n\) 的排列,满足有 \(x\) 个 \(p_i>i\),有 \(y\) 个 \(p_i>p_{i+1}\)。\(n\le 60\)。
我们设 \(dp_{i,x,y,a}\),表示我们目前扫到了 \(i\),有 \(x\) 个 \(p_i>i\),钦定了 \(y\) 个 \(p_i>p_{i+1}\),
AGC039F Min Product Sum
设 \(dp_{i,x,y}\) 表示行为 \(x\),列为 \(y\),\(\le i\) 的贡献。
UNR#7 C. 璀璨宝石
首先一定是把所有宝石拿完然后开始买发展卡。最暴力的就是 \(O(2^n)\),枚举拿发展卡顺序。
如果我们确定了买发展卡的顺序,这样子就可以确定每种宝石需要的个数。
答案就是
对于第一个特殊性质,直接设 \(dp_{i,j}\) 表示桌面上为第
设 \(dp_{i,j,k,0/1,a/b/c/d/e}\) 表示当前桌面上的发展卡是第 \(i\) 张和第 \(j\) 张,剩下状态看下文。
设计一个状态 \((k,,0,a/b/c/d/e)\) 表示有 \(k\) 个 \(a/b/c/d/e\) 未匹配,匹配个数。
设计一个状态 \((k,1,a/b/c/d/e)\) 表示当前有 \(k\) 个非 \(a/b/c/d/e\) 未匹配,匹配个数。
LGV
有一张图满足对于
QOJ4893. Imbalance
对于 \(k\le 20\),可以状压。
对于 \(k>20\),我们可以对 \(0\) 和 \(1\) 个数作 \(+-1\) 前缀和,画成折线图。
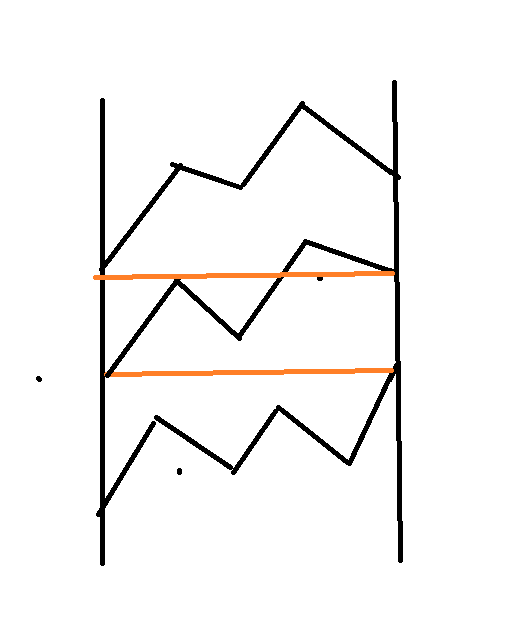
如果画成全局折线图不方便研究,可以画成周期为 \(k\) 的折线图,发现路径不相交,于是变成 LGV。
三进制 MEX 卷积
定义三进制 \(\operatorname{mex}\) 运算,先将两个数字 \(a,b\) 进行三进制拆分,形如 \(a=\sum a_i3^i\)。\(\operatorname{mex}(a,b)=\sum\limits_{i=0}^{k-1}\operatorname{mex}(a_i,b_i)\)。也就是说把每个数都拆成三进制表示,然后对于每个三进制位进行 \(\operatorname{mex}\)。
定义三进制 \(\operatorname{mex}\) 卷积为\[h_s=\sum\limits_{\operatorname{mex}(L,R)=S}f_L\times g_S \]给定长度为 \(3^{n}\) 的 \(f\) 和 \(g\),求解 \(h\)。\(n\le 10\)。
还是按照 FWT 那套方法,对于当前的最高位的值进行分类。
发现我们需要构造四种乘法,
这样子递归是 \(3^n\to 4^n\),因为三项变四项。
逆变换,令上述分别为 \(A,B,C,D\),\((A,B,C,D)\to (A,B-C,D-A-B-C)\)。
可以递归计算,时间复杂度是 \(O(n4^n)\)。
QOJ5089. 环覆盖
给定一张 \(n\) 个点,\(m\) 条边的简单无向图,对每个 \(i\in [0,m]\),计算它只保留 \(i\) 条边,使得剩下的图是一个可环覆盖图的方案数。可环覆盖的定义是,可以将边集划分成若干个子集,使得每个子集都形成一个环。
子集卷积
不相交集合的并,那么 \(j|k=i \to \lvert j\rvert+\lvert k\rvert=\lvert i\rvert\)。
\(A=A_0+A_1+...+A_n\)。\(A_i\) 包含所有 \(\lvert S\rvert=i\) 的 \(A_s\)。
\(A*B=\sum\limits_{i,j}(A_i\times B_j)\),只保留所有 \(\lvert S\rvert =\lvert i\rvert+\lvert j\rvert\) 的部分。
生成函数
题目
给定一个字符串 \(s\) 和字符集 \(r\),求有多少个长度为 \(n\) 的字符串不包含 \(s\) 作为子串。\(n\le 2\times 10^5\)。
考虑钦定 \(t\) 的若干部分为 \(s\)。这几个部分可以相交,相交长度最长为 border,记为 \(k\)。令 \(c(x)=\sum\limits_{i=1}^kx^{m-ci}\),
\(SEQ(rx-x^m\times\dfrac{1}{1+c(x)})\)。
通用测评号
假设我们最后一次操作了第一个位置的使他 \(b-1\to b\)。然后钦定 \(k\) 个 \(\ge a\)。
操作 \(n\) 次,\(\dfrac{n!}{\prod x_i!}\)
\(\dfrac{x^{b-1}}{(b-1)!}(e^x-\sum\limits_{i=0}^{a-1}\dfrac{x^i}{i!})^k(\sum\limits_{i=b}^{a-1}\dfrac{x^i}{i!})\)。
\(\sum\limits_{m}\dfrac{m!}{n^m}[x^m]F_k(x)\),将 \(n^m\) 放进去就是 \(\dfrac{x}{n}\)。\([x^m]e^{ax/n}\times x^b\)。
方格染色
对于直线多项式,线段分块多项式。
节日装饰
相对误差不超过 \(0.5\),等价于答案在 \([k,2k]\) 中时,我们直接回答 \(k\)。
我们把区间分成
我们构造一个差卷积,\(c_i=\sum\limits_{j-k=i}a_jb_k\)。
只要让 \(x_u\) 和 \(x_v\) 贡献 \(c_uc_v(c_u-c_v)^2\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号