ZR24 Summer A Day1 | Graph

PartⅠ. Flows

单位流量图跑最大流是 \(O(m\sqrt n)\)。

无源汇上下界可行流

设每条边的上下界为 \([b_i,c_i]\)。

先建立超级源点和超级汇点。我们先让所有边都流满下界，然后求出每个点净流量 \(w_i=\sum f(u,i)-\sum f(i,u)\)。如果 \(w_i>0\)，那么我们就从源点向该点连一条流量为 \(w_i\) 的边。如果 \(w_i<0\)，我们就从该点向汇点连一条 \(-w_i\) 的边。同时每条边的流量都减去下界。如果此时的最大流等于 \(\sum\limits_{w_i>0}w_i\)，那么说明可以。

CF1082G Petya and Graph

数据范围小的匹配/选择类问题考虑网络流。匹配类的套路就是把不同类的放两边跑网络流，这题就是直接把边和点各放一边跑最小割，下面是说明。

我们可以先把边权都加上也就是 \(\sum w_i\)，然后就是选点了，我们每选一个点会使得答案减少 \(a_i\)，如果一条边的两个端点没有被同时选同样会使得答案减少 \(w_i\)。

考虑最小割，我们从源点 \(s\) 向每条边连一条 \(w_i\) 的边，从每条边向两个端点各连一条 \(\infty\) 的边，同时每个点向 \(t\) 连一条 \(a_i\) 的边。

每个点和 \(s\) 联通代表被选，和 \(t\) 联通代表没有被选择了。

如果要选某点就要隔开和 \(t\) 的边使得其和 \(s\) 连通，也就要付出 \(a_i\) 的代价割开和 \(t\) 的边。选了边就必须选点，所以中间的边不可割。如果两点其一和 \(t\) 联通就要用 \(w_i\) 的代价和 \(s\) 断开，完美符合题目要求。

CF1383F Special Edges

考虑最小割，设初始所有特殊边都是可以无代价割的。

现在思考一下如何对于每组给出的 \(w_i\) 的意义，就是改变了这些边割开的代价。从原来的无代价变为需要 \(w_i\) 才能割开。

如果对于每一组 \(w\) 都跑一遍网络流，发现最后的情况一定是某些特殊边被割了，某些特殊边没有被割。考虑特殊边带来的权值，假设被割的边集为 \(S\)，我们就要付出 \(\sum\limits_{i\in S}w_i\) 的代价。

由于特殊边的个数很少，我们可以提前枚举所有边被钦定割和不割的情况，然后将可割的边设为 \(0\)，不可割的边设为 \(\infty\)，最后只需要在每次查询的时候补上 \(\sum\limits_{i\in S}w_i\) 即可。

于是就有了以下做法。

通过设置 \(\infty\) 和 \(0\) 来表示可否割。我们枚举 \(2^k\) 种所有状态，算出此时的最小割，为了快速计算可在上一次的基础上进行计算，根据网络最大流可以动态加边得知这是合法的。初始状态可以用 Dinic 来做，然后发现边权上界很小，于是每次扩展就用 FF 来做。

查询时，也是枚举 \(2^k\) 种状态，对于可割的边累加上 \(\sum\limits_{i\in S}w_i\) 即可。时间复杂度 \(O(2^kw m+q2^k)\)。

然后是这个设置 \(\infty\) 的问题，我们可以将 \(\infty\) 设为 \(25\)。虽然对于一般的网络流将 \(infty\) 设为 \(\max w\) 是不合法的，但是本题其实是可以的。如果我们在某一种方案中，选择割开了钦定不能选的边权为 \(25\) 的边，那么这种方案必定不如钦定这条边能选的方案，因为 \(w_i\le 25\)，钦定它能选带来的代价小于选择割开它的代价。

P4003 无限之环

费用流神仙题，首先为了让所有方格都流满，我们可以对于图奇偶染色，然后分别连源点和汇点，这步操作保证了相邻格子之间的流有动力进行。

对于转动次数要求，我们可以把一个点拆成五个点，中间一个点，然后周围四个点，中间点要去连源点/汇点，并且朝着有管道方向分别连流量为 \(1\)，费用为 \(0\) 的边。然后当我们旋转的时候，有一条连接上右的边的顺时针旋转 \(90°\) 后会连向下右，于是我们直接从上节点到下节点连一条费用为 \(1\) 的边即可。逆时针同理，左右节点连边。那么如果是旋转 \(180°\) 呢？我们发现已经不需要再连了，只要我们同时选择上下和左右就等价于完成了 \(180°\) 旋转。其他情况也是类似。

相邻格子之间也要连边，比如说 \((i,j)\) 的左要和 \((i,j-1)\) 的右相连。如果最后检查流满了，那么答案就是费用，否则就是 \(-1\)。

AGC031E Snuke the Phantom Thief

至多选择不太好刻画，枚举选择点的个数，于是假设我们选了 \(k\) 个点，对于点的横坐标排序后为 \(x_1,x_2...x_k\)。那么至多选择 \(t_i\) 个横坐标小于等于 \(a_i\) 的限制就可以转化为 \(x_{t_i+1}>a_i\)，对于其他几类约束同理，我们可以得到每一个数的某个坐标在一个区间里面。

然后这个时候可以忽略单调性。这是一个类似匹配的问题，将一个约束要求 \(x_{t_i+1}>a_i\)，转化为 \(X_{t_i+1}=a_i\)，然后我们要把 \(x_i\) 和 \(X\) 匹配起来。对于 \(Y\) 也要有约束，双约束要考虑建立三个区域点的图，我们可以把左边设置为 \(X_{1},X_2...X_k\)，中间为每个点 \((x_i,y_i)\)，右边为 \(Y_1,Y_2,...Y_k\)，能连边只有在点的坐标范围满足上述区间约束。跑一遍最小费用最大流即可，其中最大流保证了选出了恰好 \(k\) 个点。

AGC029F Construction of a tree

生成树可行性问题考虑用二分图的类 Hall 定理来匹配点和边。

左边点代表点集，右边点代表给出的点，每个左边的点集向它所包含的所有右边点连边。

如果对于任意一个左部点的集合 \(S\)，如果右边连向的点个数 \(< \lvert S\rvert+1\) 就代表 右边的点无法提供 \(\lvert S\rvert\) 个匹配位点，那就无法成功，否则如果对于所有左部点的集合都判定成功就可以连出树。注意 \(n\) 个点只能提供 \(n-1\) 个位点。

我们先做一个二分图的匹配，然后可以找到 \(n-1\) 个点集对应 \(n-1\) 的点。如果找不到自然是无解了。然后必然有一个节点没有被匹配到，于是我们考虑从这个点开始 dfs，遍历整张图（每一次从右到左再到右 \(u\to S_i\to v\)，都代表在树上用 \(S_i\) 集合内的点对连接了 \((u,v)\) 边），如果经过所有左边的点，那么就说明合法。如果在某个时刻无法扩展，说明对于当前已扩展集合，不满足点数 \(\ge \lvert S\rvert+1\)，那就等于找到了一个不合法的左部点集合，就无解。否则能搜到所有点，那也就是等于找到了一种合法的方案。

Gym102201J Jealous Teachers

给出一张二分图，左边 \(n-1\) 个点 \(P_i\)，右边 \(n\) 个点 \(Q_i\)，按照以下规则连边。
其中第三类边会在题中给出，问最大流能否达到 \(n(n-1)\)。
同时需要给出中间流量的方案。满足 \(n\le10^5,m\le 2\times 10^5\)。

• \((S,P_i,n)\)
• \((Q_i,t,n-1)\)
• \((P_i,Q_j,\infty)\)

直接跑最大流复杂度显然不对，应该是一个二分图匹配状物。于是先随便找一组左右 \(n-1\) 个点的匹配，然后每个点流满 \(n-1\) 的流量。然后后面的步骤和上一题好像。

此时左边每个点还多了 \(1\) 的流量，右边还有一个没匹配上的点剩余 \(n-1\) 的流量，我们要做的就是把左边 \(n-1\) 个点的流量流到右边点上去，考虑增广路，从右边点开始 dfs，可以经过左右的点，如果能达到左边的所有点就成功了。

P9726 [EC Final 2022] Magic

很巧妙的题目啊。考虑两个区间的关系，分离的话贡献是独立的不需考虑，包含的话先执行大区间再执行小区间是更优的。现在考虑两个区间相交，

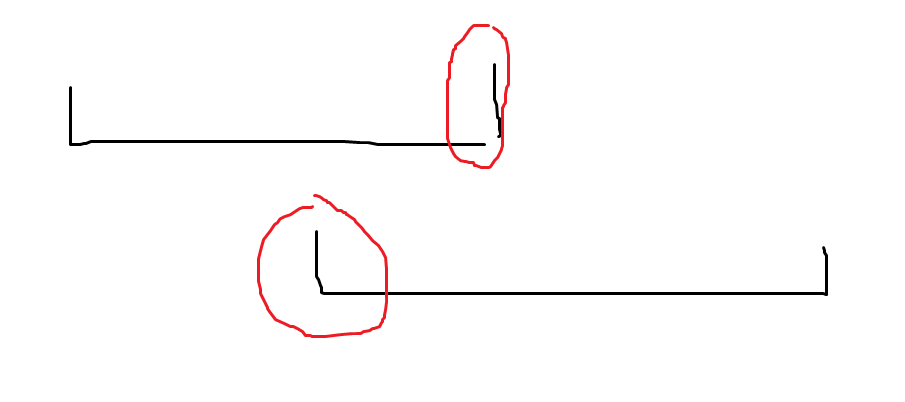
我们发现画红笔的两个地方最多只有一个产生贡献，然后有很多类似约束，于是我们可以建二分图跑最大独立集即可。

\(l_1,l_2..l_n,r_1,r_2..r_n\) 互不相同保证了图为二分图。

QOJ6508. CCPCF22H This is not an Abnormal Team!

给定一个二分图，你要把图分为大小为 \(1\) 或 \(2\) 或 \(3\) 的连通块，使得：大小为 \(1\) 的联通块数量尽量少，在此基础上大小为 \(3\) 的联通块数量尽量少。
其中数据满足 \(n\le 10^5,m\le 2\times 10^5\)。

如果只分为大小为 \(1\) 和 \(2\) 的，那就是最大匹配了。

可以发现 \(3\) 的作用是把 \(1\) 和 \(2\) 拼接起来，来消耗 \(1\)。

于是我们先跑一遍最大匹配，可以发现一个联通块内要么所有未匹配点都在左侧，要么都在右侧，否则出现增广路。

假设未匹配点都在左侧，那么这又是一个匹配的过程了，我们要将左侧的 \(1\) 块，和横跨左右的 \(2\) 块匹配起来，不妨以这个 \(2\) 块的右侧点为基准。

于是对于 \(1\) 块的点连边 \((S,u,1)\)，对于 \(2\) 块的点 \((l_u,r_u)\)，连边 \((r_u,T,1)\)，然后用 \(u\to r_v\) 的边（也就是左 \(1\) 到右 \(2\) 的连边）和 \(r_v\to l_v\) 的反悔边跑最大匹配即可。一定别忘记设置那个反悔边了！

两次都是单位边权的网络流，时间复杂度 \(O(m\sqrt n)\)。

P3227 [HNOI2013] 切糕

很重要的模型与思想。

切割之后会出现上下两部分，于是这就很像一个集合划分的问题，我们要划分上下两个点集。于是建立 \((S,id_{x,y,1},+\infty)\)，\((id_{x,y,r+1},T,+\infty)\) 和 \((id_{x,y,z},id_{x,y,z+1},v_{x,y,z})\)。

考虑处理限制，对于相邻格子中距离大于 \(D\) 的点连 \(\infty\) 的边表示无法被割开，注意这个地方要从高处往低处连。其实我们无法保证一列只被割了一条边，虽然本题建模出来其实是可以保证的，但是面对其他问题可能就不适用了，于是通法就是我们顺着链再反向连回去，建边 \((id_{x,y,r+1},id_{x,y,r},+\infty)\)，这可以让一条链切割两条边变得没有没有意义，自然也就不会去这么切了。

可以扩展为选择了距离超过 \(D\) 的时候有额外代价。

CF1630F Making It Bipartite

首先要求是一张二分图，也就是不能出现奇环。发现对于 \(3\) 个数，满足 \(a_i\mid a_j\) 且 \(a_j\mid a_k\) 的时候就会出现三元环也就不是二分图了。

于是一条倍数关系链上最多出现两个点。

考虑如何刻画这个要求，对于一个点我们对其设置一个状态 \((i,j)\) 表示在它的倍数关系链上前面有 \(i\) 个点，且它是第 \(j\) 个点。也就是说 \(j=i\) 的时候代表不选它，\(j=i+1\) 的时候代表选择它。

根据题目要求，符合条件的状态只有 \((0,0)\)，\((0,1)\)，\((1,1)\)，\((1,2)\)，\((2,2)\)。其中 \(j=i+1\) 的状态支付的代价为 \(0\)，\(i=j\) 的状态代价为 \(1\)。且呈现倍数关系的数之间的状态有约束要求，比如 \(x\mid y\) 的时候要求 \(x\) 所选状态的第二维小于等于 \(y\) 所选状态的第一维，这个要求根据我们对于这些状态的定义是可以显然得到的。

通过上一段的文字描述，我们可以发现这是一个很鲜明的切糕模型形式。

直接建图，对于单点之间各个状态的串联就按照上面所说的代价，注意为 \(0\) 代价的边我们可以直接不连了，因为在最小割中没有意义。对于各个点之间的约束，就直接对于倍数中第二维大于等于它的状态连一条 \(+\infty\) 的边即可。

CF786E ALT

二选一满足，考虑图论模型。这里建立二分图使用最小割。

左边为居民，右边为守卫，倍增优化建图跑 Dinic 即可。

然后就是最小割构造方案了，我们维护每个点在残量网络中离 \(S\) 的距离 \(dis_u\)，如果对于 \(u\)，存在 \(dis_u\)，就代表它在 \(S\) 集合，否则就在 \(T\) 集合。最后那些两个端点所属集合不同的边就是被割掉的边。

Gym103855I Marbles

有 \(n\) 个珠⼦装在了⼀些袋⼦⾥。每个珠⼦是红色或蓝色的。初始第 \(i\) 个珠⼦在第 \(i\) 个袋⼦⾥。
• 有 \(m\) 次操作：
• 1. 将两个袋⼦合并。
• 2. 第 \(i\) 个珠⼦丢失了。
• 3. 观察到某⼀个袋子里的红色珠子数量在 \([l,r]\) 内。
• 问是否有解，如果有解，输出⼀种每个珠⼦颜⾊的⽅案。
• \(n\le 2000，m\le 4000\)

很优美的一道题目。

合并两个袋子的过程就是建立一个虚点之后，两个袋子往上连虚点的过程，上下界为 \([0,\infty)\)。

如果一个袋子被观察范围是 \([l,r]\)，再被合并的时候上下界就是 \([l,r]\)，如果一个丢弃弹珠就在目前袋子向该原始点连一个 \([0,1]\) 的边。

最后会剩下若干个袋子，假设一个袋子包含了 \(\{1,4,5\}\)，那么这个袋子就向原始的 \(1,4,5\) 各连一条 \([0,1]\) 的边。

这些边的含义就是红球的数量，如果某个袋子里面有红球，它会顺着环跑一圈回来。

运行无源汇上下界可行流就行了。

P8501 [NOI2022] 二次整数规划问题

首先，约束条件可能和固有上下界产生冲突，导致区间内有些数不可能被取到，我们直接类似于 SPFA 跑 \(n\) 轮松弛一下这些约束就行了，这样子每个数在取值区间内的数都可能被取到。然后固定一些 \(l_i=r_i\) 的数，还有一些数 \(l_i\neq r_i\)，但是 \(1\in [l_i,r_i]，5\in [l_i,r_i]\)，这个时候就把 \(1,5\) 从值域中踢出去，原因会在下一段提及。

最大化的式子中可以发现，首先 \(v_1\) 和 \(v_k\) 无贡献，其次取 \(1,k\) 的时候对于 \(G\) 的贡献没有那么优。所以通过调整法，我们可以发现选 \(1\) 或选 \(k\) 不如选 \([2,k-1]\)。除了那些必须选 \(1\) 和 \(k\) 的位置外，值域可以缩小到 \([2,k-1]\)。

对于部分分，\(k=3,4\) 都可以运用基础调整法迅速得到最优解的形式。对于 \(k=3\) 的时候，能选 \(2\) 就选 \(2\)。对于 \(k=4\) 的时候，贡献函数关于未知数为线性形式，所以那些未确定数要么全选 \(2\)，要么全选 \(3\)。

对于 \(k=5\) 的时候。建议再读一遍第一段的第一步变量取值处理，然后再看这段文字。未确定数的取值有 \(\{2,3,4\}\)。首先思考约束关系，那些必定取某个值也就是 \(l_i=r_i\) 的位置如果对于未确定数产生约束的时候肯定在松弛的时候已经产生过了。比较难限制的是动区间的约束，比如两个取值为 \([2,4]\) 和 \([2,4]\) 的变量，要求距离 \(\le 1\)，也就是不能一个 \(2\)，另一个 \(4\)，在松弛那一步约束不到这里。可以发现在 \(\{2,3,4\}\) 集合内，约束为 \(1\) 的条件传递两次没有意义，因为传递两次之后就变成了距离约束为 \(2\)，而集合内部的最大距离也就是 \(2\)，所以没有用了。但是距离为 \(0\) 的约束传递多次还是紧的，可以用并查集处理。

于是，总结一下变量取值范围的约束大部分在松弛那一步已经处理完了，还有两个需要处理，一个是两个变量要求距离 \(\le 1\)（这个两个变量只可能是 \(m\) 条约束中的某个），还有一个是一些变量要求相等 （不一定为 \(m\) 条约束之一，可能是通过并查集传递的）。

处理完变量取值范围之后，我们回到最优化问题上来。可以发现贡献函数形式必定如下所示，其中 \(V_i=v_i+?\)，这个 \(?\) 代表一些距离大于 \(1\) 的变量贡献需要扣掉，反正是关于未知数是一个线性关系。

\[W=10^6(n^2-2c_2c_4)+\sum\limits_{i=2}^4c_iV_i+\lambda \]

化简式子，就是就是形如 \(-M(c_2-A_1)(c_4-A_2)+A_3\)。

令 \((c_2,c_4)\to (x,y)\)，我们需要最小化 \((x-A_1)(y-A_4)\)。

其中可以发现目前已知三个点肯定能取到，分别是 \((x_{\min},y_{\min})\)，\((x_{\min},y_{\max})\) 和 \((x_{\max},y_{\min})\)。\(x_{\min}\) 就是只有那些松弛过后 \(l_i=r_i\) 的点产生贡献，\(x_{\max}\) 则是把所有 \(2\in[l_i,r_i]\) 的点都压到了 \(2\)，保证能取到是因为这些动区间点聚集在一起之后距离肯定为 \(0\) 也就肯定满足约束，而剩下点还是那一句话定点对于动区间点的约束已经在松弛一步约束过了，所以这三个点肯定能取到。

我们现在需要处理出一个可能取到最优答案的点集，遇到哪个询问，就直接对于点集内所有点代入算一遍看看哪个最优就行了。你直接把所有可能的合法点放入这个点集，显然复杂度是要爆的。因此我们需要挑出一些有用的点放入，一些 \(100\%\) 不可能产生贡献的点就不放进去了。

题目要处理的就是平移之后的 \(x'y'\) 乘积最小值。可以发现如果平移之后，还存在点处于 \(1,2,4\) 象限，那么肯定包含上面三个定点之一，选择它们是最好的（这个可以自己画画图就能看出来）。因此先把这三个点纳入点集。

问题是如果所有点都被移动到了第三象限怎么办？乘法之后负负得正，我们可以作出判断，只有上凸壳上面的点是有效的（注意如果是 \(x,y>0\) 那么是下凸壳，但是这里 \(x,y<0\)，所以是上凸壳）。

根据引理，

在一个 \(V\times V\) 的矩形上，凸包点的个数是 \(O(V^{\frac{2}{3}})\) 的。

于是我们就把有用点点集大小缩小到了凸包大小量级，也就是 \(O(V^{\frac{2}{3}})\)。

可惜我们无法直接显式建立这个凸包。不过根据 P5540 的 trick，我们可以解决这个凸包问题。我们知道凸包上的两点 \(P(x_{\min},y_{\max})\) 和 \(Q(x_{\max},y_{\min})\)。我们可以通过已有的两点去构建这个凸包，直接寻找所有点还是不容易，考虑哪个点是一定在凸包上的，那么就是一个点 \(R\) 满足在直线 \(PQ\) 上方且离 \(PQ\) 距离最大。找到 \(R\) 点之后更新答案，并且分治为 \((P,R)\) 和 \((R,Q)\) 去解决问题，这样子我们每次找到一个肯定在凸包上的点，总的寻找复杂度也就是凸包上点的个数乘以单次寻找时间复杂度。

现在考虑如何找到 \(R\) 点，上述条件等价于三角形 \(PQR\) 的面积最大，也就是 \(\vec{RP}\times \vec{RQ}\) 最大。代入坐标，利用叉乘公式计算之后可以得到，希望最大化 \((X_Q-X_P)y_R+(Y_P-Y_Q)x_R\)，也就是最小化 \((X_P-X_Q)y_R+(Y_Q-Y_P)x_R\)。

也就是说每个数如果选 \(2\) 就会有 \(Y_Q-Y_P\) 的代价，如果选 \(4\) 就会有 \(X_P-X_Q\) 的贡献，选 \(3\) 没有贡献，同时一些数之间会有在上文中的两个约束。这显然是一个切糕模型的形式。每次利用切糕模型建图，代价可能是负的，平移 \(n\) 即可。跑最小割即可。利用最小割的流量信息求出一组方案，然后找到凸壳上的点，继续分治就行了。注意找到点之后要验证其是否在凸包上，以防复杂度退化。

时间复杂度 \(O(n^{\frac{2}{3}}(q+\rm Dinic()))\)。

PartⅡ. 2-sat

AGC059C Guessing Permutation for as Long as Possible

对于具有先后顺序的三组询问，\((a,b)~(b,c)~(a,c)\)，我们可以得出 \(b>a\wedge b>c\) 或 \(b<a \wedge b<c\)。可以发现这是一个 2-SAT 的形式，因此我们仿照 2-SAT 的建图方式建图。

对于三元组 \((a,b,c)\)，假设其第一次出现的询问是 \((a,b)\)，我们就将其拆成 \(a>b\) 和 \(a<b\)。然后将 \(a<b\) 和 \(b>c\) 连边，同时将 \(a>b\) 和 \(c>b\) 连边。这是双向边，直接并查集。需要满足 \(a<b\) 和 \(a>b\) 不在同一联通块内。

设最后连通块个数为 \(c\)，答案就是 \(2^{\frac{c}{2}}\)，因为一个某个联通块确定之后其相反联通块也会被确定，所以需要除以二。

CF587D Duff in Mafia

考虑二分答案之后转化为判定，由于每条边只有选和不选两种状态，所以可以用 2-SAT。

记录 \(id_{i,0}\) 表示第 \(i\) 条边不选，\(id_{i,1}\) 则表示选。

首先，对于边权大于 \(mid\) 的边，\(id_{i,1}\to id_{i,0}\)，表示不可选。

然后，对于一个点的连边形态有要求，对一个点其边中至多一种颜色出现了 \(2\) 次，其余均为 \(\le 1\) 次。

对于第一种情况，我们要求必须删这个出现两次颜色的边的其中一个，于是对于其他边 \(id_{i,1}\to id_{i,0}\) 表示不可删，对于这两条边 \(id_{i,1}\to id_{j,0}\)，\(id_{i,0}\to id_{j,1}\)，\(id_{j,0}\to id_{i,1}\)，\(id_{j,1}\to id_{j,0}\)。

对于第二种情况，我们可以选择删除至多一条边，也可以不删。于是 \(id_{i,1}\to id_{j,0}\)，但是这么连对于单个点会有 \(O(deg^2_u)\) 条边，可以用前后缀优化建图优化掉。时间复杂度 \(O((n+m)\log V)\)。

Part.Ⅲ Graph Theory

圆方树

可以对于点双连通分量相关题目建立圆方树。

对于一个点双联通分量建立一个方点，对于所有原图上的点建圆点，将方点与其包含的原图上的点所建圆点连边。所有非叶子圆点为割点。圆点连方点，方点连圆点。

CF1137C Museums Tour

把一个拆成 \(d\) 个点，分别代表在一周之内的某一天到达某个博物馆。

先 tarjan 一下，求出每个 scc 之内有几个博物馆，然后直接跑最长路 dp 就行了。

正确性是由于一个博物馆的两个状态不可能只有单向可达性，假如 \((x,0)\to (x,a)\)，那么 \((x,a)\to (x,a+a)\)，以此类推可以得到 \((x,a)\to (x,a\times d)\)，在模 \(d\) 的意义下就是 \((x,0)\)，所以二者在同一 scc 中只会被统计一次。

无来源

有一个 \(n\) 个点的图，初始没有边，接下来有 \(m\) 条边依次加入，保证无自环，任意两点最多一条边。每次加边后求出如果将该图补成竞赛图后，强连通分量个数的最小值。\(n\le 2\times 10^5,m\le 2\times 10^6\)。

结论：补图中一个联通块可以通过加边定向成一个强连通分量（唯一反例是连通块大小为 \(2\)）。

初始所有点都在一个强联通分量中，不过给某些边定下来了方向，所以强联通块数量会增加，这是一个分裂的过程不好处理。考虑倒序，不断给原图删边，相当于给补图加边，是强联通分量合并的过程，比较好处理。

所以先处理加入 \(m\) 条边之后的情况，求出此时补图中的所有联通块（依次处理所有未被加入点，标记当前点的所有出点，把剩下点拿走放进同一联通块内，注意特判两个点），然后用当前的 \(m\) 条边跑一次 tarjan 就可以得到所有 scc。由于这是一个竞赛图，所以 scc 的关系是一条链，每次删除一条边，就相当于我们可以给补图中的一条边定向，如果这条边无影响就不管，否则就就是合并 scc 链上的一个区间。

由于最多只会有 \(O(\sqrt m)\) 个强联通分量，所以可以直接暴力合并。

P5811 [IOI2019] 景点划分

不妨设 \(a\le b\le c\)。由于我们可以从大联通块中不断删叶子节点得到小联通块，所以我们发现小联通块是更好构造的，于是我们就是要找到两个大小分别为 \(a\) 和 \(b\) 的联通块。把剩下点分配给 \(c\) 即可。

我们需要尽可能均匀分配，所以联想到重心。对于树，我们找到重心，如果重心的一个最大子树 \(\ge a\)，就有解。否则无解。因为重心的任意一个子树大小都是 \(\le \dfrac{n}{2}\)。而 \(a\le b\le c\) 保证了 \(b\le \dfrac{n}{2}\)，所以如果能找到这么一个子树，那么剩下点给 \(b\) 用一定合法。反之如果找不到的话，那么 \(a\) 就必须占据重心位置，而 \(b\) 只能选择重心的某个子树，由于 \(\rm {maxsize} < a\le b\)，所以矛盾了。

对于非树，我们先找到一个 dfs 树，找到 dfs 树的重心，如果能找到一个子树大小 \(\ge a\) 还是可以同理构造。否则我们可以利用返祖边，首先添加 \(u\) 上方子树，不断添加 \(u\) 下方的与 \(u\) 上方子树有连边的子树，直到大小 \(\ge a\)，由于之前的 \(\rm {maxsize}<a\)，所以当前联通块大小 \(<2a\)，\(n-2a\ge b\)，故一定合法。

QOJ3301. Economic One-way Roads

需要找到一个刻画强联通图的方式，这里用耳分解，可以从一个点出发不断通过加一个环的一部分（起点和终点都在已加入的集合里）的方式来得到一个强联通分量。

我们设 \(f_s\) 表示通过耳分解得到 \(S\) 的最小代价，转移的时候枚举另外一个集合 \(T\) 表示加入集合，这个复杂度太高了。我们改一下，设 \(g_{s,u,v}\) 表示在 \(S\) 集合时，目前的耳构造到了 \(u\)，我们的终点是 \(v\) 的最小代价。

枚举集合 \(S\)，首先可以在扩展途中闭合一个环，就是用 \(g_{s,i,j}+G_{i,j}\) 更新答案 \(f_s\)。其中必须满足 \(i,j \in S\) 表示已经构造到最后一步了然后用边 \((i,j)\) 连接。然后需要注意一个点，就是我们求出 \(f_s\) 之后，应该用 \(f_s\) 反向更新 \(g_{s,i,j}\)。然后再用 \(g_{s,i,j}\) 向外扩展，枚举 \(u\)，\(g_{s\cup{u},u,j} \gets g_{s,i,j}+G_{i,u}\)。还有一个细节就是如果 \(i=j\)，我们要是只往外扩展一个点，可能会出现更新 \(g\) 时用 \(i\to u\)，然后更新答案的时候又用 \(u\to i\)，这就代表一条边被正反使用了，不符合要求，于是当 \(i=j\) 的时候，我们应该寻找两个不同 \(u\) \(v\) 强制将两个端点转到 \(u\) \(v\) 这样就行了，时间复杂度 \(O(2^nn^3)\)。

注意细节由于 dp 的时候是只加入对于强连通分量有贡献的边，但是这并不代表其他边不要定向，所以我们应该提前按照费用小的那边先给所有边定向，然后记录一下费用大的边翻转的费用。

P5807 【模板】BEST 定理 | Which Dreamed It

\(1\) 为起点，除了起点，其他点的最后一条出边不形成环，所以所有最后一条出边就是以 \(1\) 为根的内向树，钦定完了最后一条出边之后，剩下的边以任意顺序访问，是一个阶乘的形式。

因此有向图的欧拉回路个数：\(\prod\limits_u(deg_u-1)!\times\) 以某点为根的内向树个数

注意上述情况是没有指定根的情况，去掉了循环同构。如果固定了起点的话，就是 \(deg_1 !\) 了，所以我们需要额外 \(\times deg_1\)。

直接套用 Matrix-Tree 定理即可。

QOJ8056. Travel 2

\(2m+2n\) 是每条边都遍历两次，还有搜索树上每条边都遍历两次的量级。

考虑直接对于所有点暴搜，按照编号从小到大搜所有出边。但是直接这么搜会漏边，比如可能某个点还没搜完就回去之前的点了，使得某些点没到达。

考虑第一次进入每个点的边，显然这些边构成了一颗搜索树。

注意到上面说到的漏边情况，只有可能发生在从某个点回到了其搜索树父亲的时候才会发生。于是我们只需要顺着搜索树再搜一遍就行了。

所以某个点如果其所有出边都被遍历过了，且又回到了该点，那么对于该点标记一下。此时我们得到了其所有出边信息，所以直接遍历其所有出边，对于没有被标记的点 dfs 去继续搜出边。

第一部分的次数是每条边正反搜两次是 \(2m\)，第二部分是搜索树的边正反搜两次是 \(2(n-1)\)。

UOJ670.获奖名单

如果全部长度为 \(2\) 的话，直接两两匹配即可。我们采取左右交替放置的策略，考虑如果出现了一个长度为 \(1\) 的段和若干长度为 \(2\) 的段，当长度 \(1\) 段放置后之后再放 \(2\) 的时候，必然是另一边已经确定了一个字母，这样子不断左右构造。考虑图论建模，对于长度为 \(1\) 的段 \(u\)，建立 \((u,S)\)，对于长度为 \(2\) 的段 \(u~v\)，我们建立 \((u,v)\)，注意以上均为无向边，这样子长度为 \(2\) 的段如果反着走就代表翻着了。

所有长度为 \(1\) 的串所形成的边都在 \(S\) 联通块内。

对于长度为偶数的串，需要 \(S\) 所在联通块存在欧拉回路，其他联通块每种边出现两次，这样子就可以欧拉回路构造出一个回文，其他联通块内通过两两匹配构造回文。

对于长度为奇数的串，把上述的欧拉回路改为欧拉路径即可，这样子就能凑出奇数长度了。