线性同余生成器 (LCG)
线性同余生成器 (LCG)
概念
线性同余方法(LCG)是个产生伪随机数的方法
LCG的性能和随机性取决于选取的参数。如果选择恰当的参数,LCG可以生成长周期和均匀分布的伪随机数序列。然而,不恰当的参数选择可能导致序列的周期较短或者存在可预测的模式,从而影响其随机性和安全性
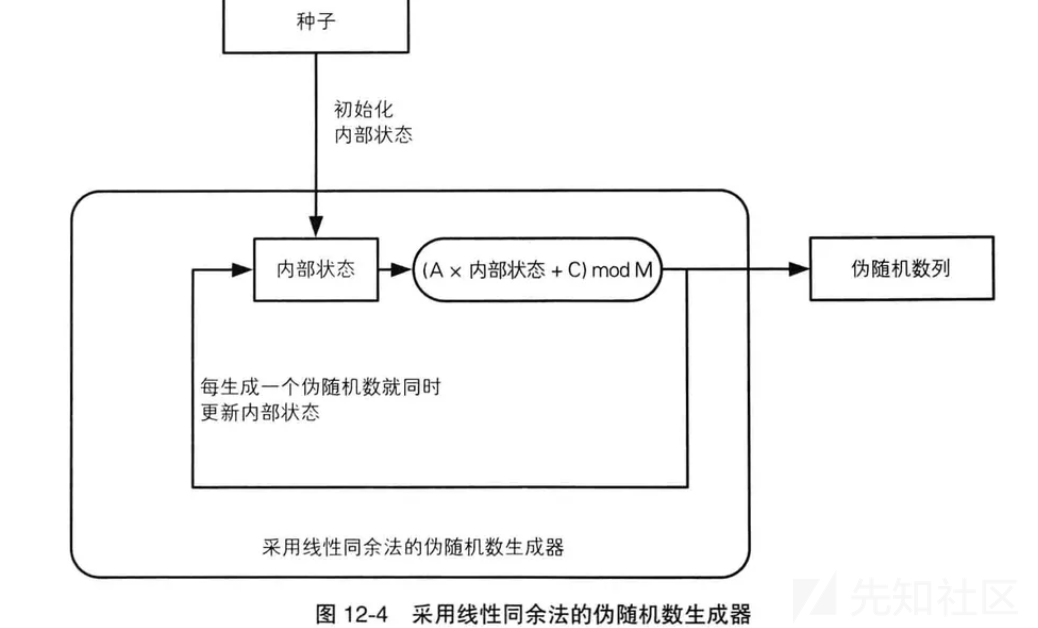
LCG的周期最大为 M,但大部分情况都会少于 M。要令LCG达到最大周期,应符合以下条件:
1.B,M 互质;
2.M 的所有质因数都能整除 A-1
3.若 M 是4的倍数,A-1 也是
4.A,B,N0 都比 M 小
5.A,B 是正整数
from functools import reduce
from math import gcd
from Crypto.Util.number import *
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % m
def crack_unknown_increment(states, modulus, multiplier):
increment = (states[1] - states[0]*multiplier) % modulus
return modulus, multiplier, increment
def crack_unknown_multiplier(states, modulus):
multiplier = (states[2] - states[1]) * modinv(states[1] - states[0], modulus) % modulus
return crack_unknown_increment(states, modulus, multiplier)
def crack_unknown_modulus(states):
diffs = [s1 - s0 for s0, s1 in zip(states, states[1:])]
zeroes = [t2*t0 - t1*t1 for t0, t1, t2 in zip(diffs, diffs[1:], diffs[2:])]
modulus = abs(reduce(gcd, zeroes))
return crack_unknown_multiplier(states, modulus)
# N[i+1] = (A*N[i]+B) % M
# A,B,N均未知
sequence = []
modulus, multiplier, increment = crack_unknown_modulus(sequence)
print('A = '+str(multiplier))
print('B = '+str(increment))
print('N = '+str(modulus))
公式及推论
公式
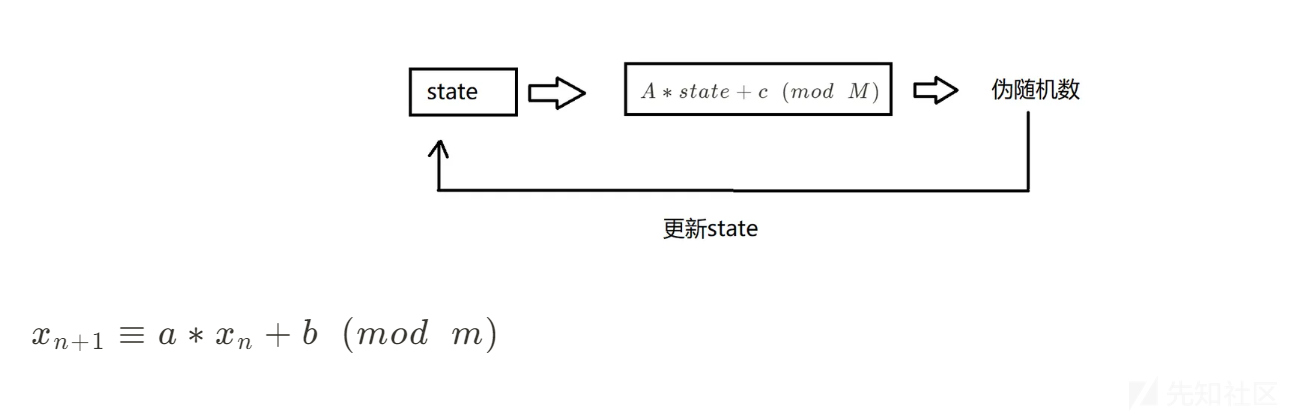
推论


基础题目分析
lcg_1
from Crypto.Util.number import *
flag = b'Spirit{***********************}'
plaintext = bytes_to_long(flag)
length = plaintext.bit_length()
a = getPrime(length)
b = getPrime(length)
n = getPrime(length)
seed = 33477128523140105764301644224721378964069
print("seed = ",seed)
for i in range(10):
seed = (a*seed+b)%n
ciphertext = seed^plaintext
print("a = ",a)
print("b = ",b)
print("n = ",n)
print("c = ",ciphertext)
# seed = 33477128523140105764301644224721378964069
# a = 216636540518719887613942270143367229109002078444183475587474655399326769391
# b = 186914533399403414430047931765983818420963789311681346652500920904075344361
# n = 155908129777160236018105193822448288416284495517789603884888599242193844951
# c = 209481865531297761516458182436122824479565806914713408748457524641378381493
seed,a,b,n,lcg所有参数都已知,逆回去就好
from Crypto.Util.number import *
seed = 33477128523140105764301644224721378964069
a = 216636540518719887613942270143367229109002078444183475587474655399326769391
b = 186914533399403414430047931765983818420963789311681346652500920904075344361
n = 155908129777160236018105193822448288416284495517789603884888599242193844951
c = 209481865531297761516458182436122824479565806914713408748457524641378381493
print("seed = ",seed)
for i in range(10):
seed = (a*seed+b)%n
flag = seed^c
print(long_to_bytes(flag))
#b'Spirit{0ops!___you_know__LCG!!}'
lcg_2
from Crypto.Util.number import *
flag = b'Spirit{*****************************}'
plaintext = bytes_to_long(flag)
length = plaintext.bit_length()
a = getPrime(length)
b = getPrime(length)
n = getPrime(length)
seed = plaintext
for i in range(10):
seed = (a*seed+b)%n
ciphertext = seed
print("a = ",a)
print("b = ",b)
print("n = ",n)
print("c = ",ciphertext)
# a = 59398519837969938359106832224056187683937568250770488082448642852427682484407513407602969
# b = 32787000674666987602016858366912565306237308217749461581158833948068732710645816477126137
# n = 43520375935212094874930431059580037292338304730539718469760580887565958566208139467751467
# c = 8594514452808046357337682911504074858048299513743867887936794439125949418153561841842276
flag就是seed,已知a,b,n,c求seed,即推论1
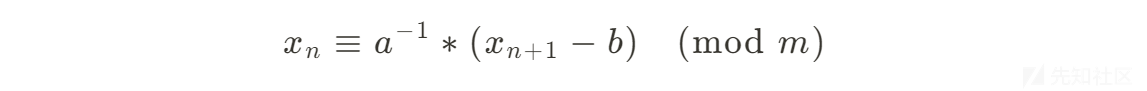
from Crypto.Util.number import *
a = 59398519837969938359106832224056187683937568250770488082448642852427682484407513407602969
b = 32787000674666987602016858366912565306237308217749461581158833948068732710645816477126137
n = 43520375935212094874930431059580037292338304730539718469760580887565958566208139467751467
c = 8594514452808046357337682911504074858048299513743867887936794439125949418153561841842276
seed=c
for i in range(10):
seed=(inverse(a,n)*(seed-b))%n
flag=seed
print(long_to_bytes(flag))
#b'Spirit{Orzzz__number_the0ry_master!!}'
lcg_3
from Crypto.Util.number import *
flag = b'Spirit{*********************}'
plaintext = bytes_to_long(flag)
length = plaintext.bit_length()
a = getPrime(length)
seed = getPrime(length)
n = getPrime(length)
b = plaintext
output = []
for i in range(10):
seed = (a*seed+b)%n
output.append(seed)
ciphertext = seed
print("a = ",a)
print("n = ",n)
print("output1 = ",output[6])
print("output2 = ",output[7])
# a = 3227817955364471534349157142678648291258297398767210469734127072571531
# n = 2731559135349690299261470294200742325021575620377673492747570362484359
# output1 = 56589787378668192618096432693925935599152815634076528548991768641673
# output2 = 2551791066380515596393984193995180671839531603273409907026871637002460
知道两个连续的随机数,已知a,n,推论3
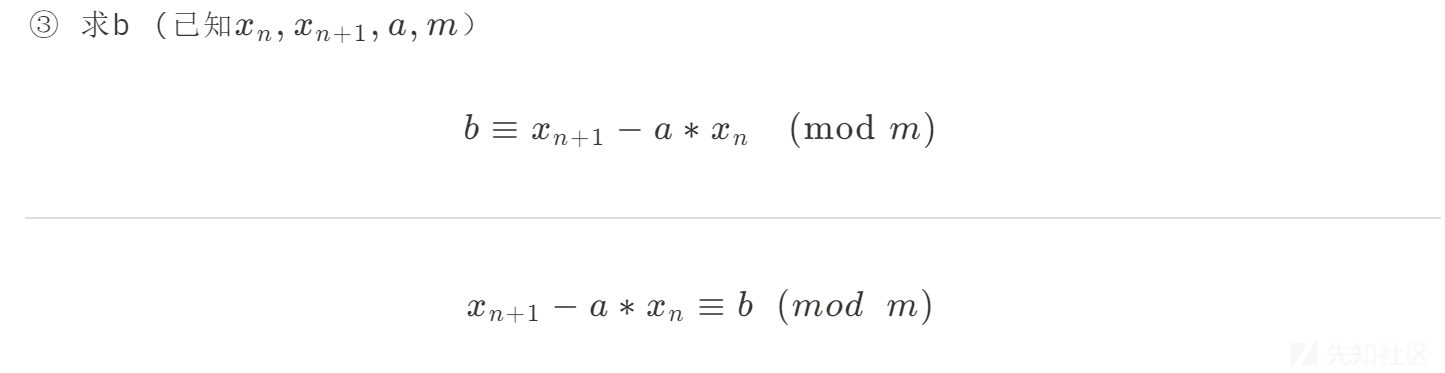
b→flag
from Crypto.Util.number import *
a = 3227817955364471534349157142678648291258297398767210469734127072571531
n = 2731559135349690299261470294200742325021575620377673492747570362484359
output1 = 56589787378668192618096432693925935599152815634076528548991768641673
output2 = 2551791066380515596393984193995180671839531603273409907026871637002460
b=(output2-a*output1)%n
print(long_to_bytes(b))
#b'Spirit{Y0u_@r3_g00d_at__math}'
lcg_4
from Crypto.Util.number import *
flag = b'Spirit{********************************}'
plaintext = bytes_to_long(flag)
length = plaintext.bit_length()
a = getPrime(length)
b = getPrime(length)
n = getPrime(length)
seed = plaintext
output = []
for i in range(10):
seed = (a*seed+b)%n
output.append(seed)
print("n = ",n)
print("output = ",output)
# n = 714326667532888136341930300469812503108568533171958701229258381897431946521867367344505142446819
# output = [683884150135567569054700309393082274015273418755015984639210872641629102776137288905334345358223, 285126221039239401347664578761309935673889193236512702131697050766454881029340147180552409870425, 276893085775448203669487661735680485319995668779836512706851431217470824660349740546793492847822, 670041467944152108349892479463033808393249475608933110640580388877206700116661070302382578388629, 122640993538161410588195475312610802051543155060328971488277224112081166784263153107636108815824, 695403107966797625391061914491496301998976621394944936827202540832952594905520247784142392337171, 108297989103402878258100342544600235524390749601427490182149765480916965811652000881230504838949, 3348901603647903020607356217291999644800579775392251732059562193080862524671584235203807354488, 632094372828241320671255647451901056399237760301503199444470380543753167478243100611604222284853, 54758061879225024125896909645034267106973514243188358677311238070832154883782028437203621709276]
flag→seed

from Crypto.Util.number import *
n = 714326667532888136341930300469812503108568533171958701229258381897431946521867367344505142446819
output = [683884150135567569054700309393082274015273418755015984639210872641629102776137288905334345358223, 285126221039239401347664578761309935673889193236512702131697050766454881029340147180552409870425, 276893085775448203669487661735680485319995668779836512706851431217470824660349740546793492847822, 670041467944152108349892479463033808393249475608933110640580388877206700116661070302382578388629, 122640993538161410588195475312610802051543155060328971488277224112081166784263153107636108815824, 695403107966797625391061914491496301998976621394944936827202540832952594905520247784142392337171, 108297989103402878258100342544600235524390749601427490182149765480916965811652000881230504838949, 3348901603647903020607356217291999644800579775392251732059562193080862524671584235203807354488, 632094372828241320671255647451901056399237760301503199444470380543753167478243100611604222284853, 54758061879225024125896909645034267106973514243188358677311238070832154883782028437203621709276]
#求a
x0=output[0]
x1=output[1]
x2=output[2]
a=((x2-x1)*inverse((x1-x0),n))%n
print("a=",a)
#求b
b=(x1-a*x0)%n
print("b=",b)
seed=output[-1]
for i in range(10):
seed = (inverse(a,n)*(seed-b))%n
print(long_to_bytes(seed))
# a= 65863586327872307178215811859890622391386702699190067821678721759311822315235571722857932007760
# b= 580530341837176922585879619790971707330065277035664726870365931385222825590112557483074386629351
# b'Spirit{Gr3at__J0b!_You_can_be___better!}'
lcg_5
from Crypto.Util.number import *
flag = b'Spirit{****************************************}'
plaintext = bytes_to_long(flag)
length = plaintext.bit_length()
a = getPrime(length)
b = getPrime(length)
n = getPrime(length)
seed = plaintext
output = []
for i in range(10):
seed = (a*seed+b)%n
output.append(seed)
print("output = ",output)
# output = [9997297986272510947766344959498975323136012075787120721424325775003840341552673589487134830298427997676238039214108, 4943092972488023184271739094993470430272327679424224016751930100362045115374960494124801675393555642497051610643836, 6774612894247319645272578624765063875876643849415903973872536662648051668240882405640569448229188596797636795502471, 9334780454901460926052785252362305555845335155501888087843525321238695716687151256717815518958670595053951084051571, 2615136943375677027346821049033296095071476608523371102901038444464314877549948107134114941301290458464611872942706, 11755491858586722647182265446253701221615594136571038555321378377363341368427070357031882725576677912630050307145062, 7752070270905673490804344757589080653234375679657568428025599872155387643476306575613147681330227562712490805492345, 8402957532602451691327737154745340793606649602871190615837661809359377788072256203797817090151599031273142680590748, 2802440081918604590502596146113670094262600952020687184659605307695151120589816943051322503094363578916773414004662, 5627226318035765837286789021891141596394835871645925685252241680021740265826179768429792645576780380635014113687982]
和上一题一样,但是n不知道,多了一步求n (推论4求m (已知多组x))
from Crypto.Util.number import *
import gmpy2
output = [9997297986272510947766344959498975323136012075787120721424325775003840341552673589487134830298427997676238039214108, 4943092972488023184271739094993470430272327679424224016751930100362045115374960494124801675393555642497051610643836, 6774612894247319645272578624765063875876643849415903973872536662648051668240882405640569448229188596797636795502471, 9334780454901460926052785252362305555845335155501888087843525321238695716687151256717815518958670595053951084051571, 2615136943375677027346821049033296095071476608523371102901038444464314877549948107134114941301290458464611872942706, 11755491858586722647182265446253701221615594136571038555321378377363341368427070357031882725576677912630050307145062, 7752070270905673490804344757589080653234375679657568428025599872155387643476306575613147681330227562712490805492345, 8402957532602451691327737154745340793606649602871190615837661809359377788072256203797817090151599031273142680590748, 2802440081918604590502596146113670094262600952020687184659605307695151120589816943051322503094363578916773414004662, 5627226318035765837286789021891141596394835871645925685252241680021740265826179768429792645576780380635014113687982]
def find_gcd(numbers): #求c中各元素的最大公约数
result = numbers[0]
for num in numbers[1:]:
result = gcd(result, num)
return result
#求n
t = []
for i in range(9):
t.append(output[i]-output[i-1])
all_n = []
for i in range(7):
tt=gcd((t[i+1]*t[i-1]-t[i]*t[i]), (t[i+2]*t[i]-t[i+1]*t[i+1]))
if tt>2**5:
all_n.append(tt)
n=find_gcd(all_n)
#求a
x0=output[0]
x1=output[1]
x2=output[2]
a=((x2-x1)*inverse((x1-x0),n))%n
#求b
b=(x1-a*x0)%n
seed = (inverse(a,n) * (x0 - b)) % n
print(long_to_bytes(seed))
#b'Spirit{final__lcg__is__co0m1ing__are_you_ready?}'


 浙公网安备 33010602011771号
浙公网安备 33010602011771号