Coppersmith 小根攻击解决ACD问题（the Approximate Common Divisor Problem）

我在打H&NCTF的factor题目碰到了这样的题目，所以想着探究一下。比赛当时我是参考2024-高校密码挑战赛赛题一-wp-crypto | 糖醋小鸡块的blog

得到了灵感。但是我不知道选取参数\(t=20,k=10\)到底有什么用，为什么能规约出243bit呢？

一：前言

如果说我们知道 \(x1,⋯,xl\) 满足:

\(x1=p*q1\) (1)

\(x2=p*q2\) (2)

……

\(xl=p*ql\)

那么我们想要获得 p，仅需要求最大公约数即可，即p=gcd(x1,⋯,xl),用辗转相除法可以很容易得出。

但是如果加上一个参数呢？

\(xl=p*ql+rl\)

如果r很小，那么可以尝试去爆破\(p=gcd(x1-r1,x2-r2)\)得到p

那如果r很大呢，显然就不现实了

二：原理

Coppersmith 小根攻击在 hint = A·p + r 模型中的应用

题目中，RSA 模数为：

N = p * q

同时泄露了如下构造的 hint：

hint = A * p + r

其中：

  • p 是 RSA 的一个素因子；
  • A 是已知的大素数；
  • r 是一个小整数（目标恢复对象）；
  • 已知 hint、N，目标是通过恢复 r 进一步恢复 p。

已知：

\[\text{hint} \equiv r \pmod{p} \quad \Rightarrow \quad f(r) \equiv 0 \pmod{p} \]

我们构造多项式：

\(f(x) = \text{hint} - x\)

显然，如果我们能找到一个满足 f(r) ≡ 0 mod p 且 r 足够小的根，就可以通过 Coppersmith 方法将其恢复。

Coppersmith 一元小根攻击原理简述

Coppersmith 提出了以下结论：

对任意模数 \(N\)，若一元多项式 \(f(x)\) 有一个小根 \(r\) 满足 \(f(r) \equiv 0 \pmod{N}\)，且 \(|r| < N^{1/d}\)（其中 \(d\) 是多项式的次数），那么可以在多项式系数构成的格（lattice）中找到对应的根。

格的构造方法

为了使用格规约（LLL 算法）恢复 \(r\)，我们将 \(f(x)\) 构造为一系列多项式：

\[f_i(x) = f(x)^i \cdot N^{\max(k - i, 0)} \quad \text{for } i = 0, 1, \ldots, t \]

其中参数含义如下：

  • \(t\)：控制多项式个数（构造 \(t+1\) 个）；
  • \(k\)：控制每个多项式中模数 \(N\) 的幂次，保证整除性；
  • \(R\)：我们估计 \(r\) 的最大值，即 \(R = 2^{\text{rbit}}\)。

将所有 \(f_i(x)\) 展开后得到 monomials，将它们作为向量坐标轴构造整数系数矩阵 \(L\)，再通过 LLL 进行规约，提取出一个“短向量”，它实际编码了某个整系数多项式 \(h(x)\)，满足：

\[h(x) \equiv 0 \pmod{N} \quad \text{且} \quad h(r) = 0 \]

我们最终对 \(h(x)\) 求解根即可得到 \(r\)。

参数选择建议

参数 意义 推荐值 说明
\(t\) 多项式个数控制 10–30 增大提升格规约成功率，但会变慢
\(k\) 控制模数 \(N\) 的参与程度 \(t//2\) 保证整除性，同时维持格结构合理
\(R\) 目标根的最大值估计 \(2^{rbit}\) 越大代表攻击越难成功

理论上，小根攻击可行的上界为：

\(|r| < N^{1/d}\)

在实际实验中，N = 1024 位时，使用 \(t=20\), \(k=10\) 通常可以成功恢复 \(r\) 为 240–245 位的整数。

脚本结构概览

攻击流程总结如下：

  1. 构造 \(f(x) = \text{hint} - x\)
  2. 构造一组 \(f_i(x) = f^i \cdot N^{\max(k-i, 0)}\)
  3. 将这些多项式的 monomial 系数矩阵化，构成格矩阵 \(L\)
  4. 使用 LLL 对 \(L\) 规约，得到整系数多项式 \(h(x)\)
  5. 解 \(h(x) = 0\) 得到 \(r\)，从而计算 \(p = gcd(\text{hint} - r，N)\)

脚本如下：

from Crypto.Util.number import getPrime
from sage.all import *
from tqdm import tqdm

Nbits = 1024
p = getPrime(Nbits // 2)
q = getPrime(Nbits // 2)
N = p * q

A = getPrime(Nbits // 2)

start_bit = 200
end_bit = 280
step = 5

print("Coppersmith 小根恢复实验")
print("-" * 60)
for rbit in tqdm(range(start_bit, end_bit + 1, step), desc="正在测试 rbit 位数", unit="bit"):
    r = getPrime(rbit)
    hint = A * p + r

    R = 2^rbit
    x = ZZ['x'].gens()[0]
    f = hint - x  # f(x) = hint - x

    t, k = 20, 10
    polynomials = []
    monomials = set()

    for i in range(t + 1):
        poly = (f)^i * N^max(k - i, 0)
        polynomials.append(poly)
        monomials.update(poly.monomials())

    monomials = sorted(list(monomials), key=lambda m: m.degree())
    L = Matrix(ZZ, len(polynomials), len(monomials))

    for i, poly in enumerate(polynomials):
        for j, m in enumerate(monomials):
            L[i, j] = poly.monomial_coefficient(m) * (R^m.degree())

    try:
        L_red = L.LLL()
    except:
        tqdm.write(f"[!] LLL failed at rbit = {rbit}")
        continue

    h = 0
    for j, m in enumerate(monomials):
        h += (L_red[0][j] // (R^m.degree())) * m

    try:
        h = h.change_ring(QQ).monic()
        roots = h.roots()
    except:
        tqdm.write(f"[!] Monic or roots() failed at rbit = {rbit}")
        continue

    if roots:
        tqdm.write(f"[√] Success at rbit = {rbit:3d} | recovered r = {int(roots[0][0])}")
    else:
        tqdm.write(f"[×] Fail    at rbit = {rbit:3d} → 后续终止")
        break

我的建议是先用大step，后面在哪个位置停住了就确定范围，再令step=1

攻击成功与否的判断

  • 若 LLL 成功规约出 \(h(x)\) 并找到根 \(r\)，说明攻击成功；
  • 若失败，说明当前设置下无法规约出如此大的 \(r\)，应降低 rbit 或提高 \(t,k\) 继续尝试；
  • 实验中，一旦某个 rbit 失败，后续更大的 rbit 理论上也不可能成功，可以提前停止测试。

恢复r

只要得到能够规约的bits，后面的就参考糖醋小鸡块师傅的攻击方法，结合copper解决

from Crypto.Util.number import *
from tqdm import *
from itertools import *
from multiprocessing import Pool

################################################ gen data
e = 
N = 
c = 
m = 1
rho =    #能够规约的最大值
a = ["pad"] + [hint]


def attack(ii):
    a = ["pad"] + [hint - 2^rho*ii]

    ################################################ params
    t,k = 20,10 #上面得到的参数
    R = 2^rho
    indices = []
    for i in product([i for i in range(t+1)] , repeat=m):
        if(sum(list(i)) <= t):
            indices.append(["pad"] + list(i))


    ################################################ attack
    PR = ZZ[tuple(f"X{i}" for i in range(m))]
    X = ["pad"] + list(PR.gens())
    poly = []
    monomials=set()
    for i in indices:
        f = 1
        for ij in range(1,len(i)):
            f *= (X[ij] - a[ij])^i[ij]
        l = max(k-sum(i[1:]),0)
        f *= N^l
        poly.append(f)
        for mono in f.monomials():
            monomials.add(mono)


    ################################################# LLL and resultant to find roots
    L = Matrix(ZZ,len(poly),len(monomials))
    monomials = sorted(monomials)
    for row,shift in enumerate(poly):
        for col,monomial in enumerate(monomials):
            L[row,col] = shift.monomial_coefficient(monomial)*monomial(*([R]*m))


    res = L.LLL()
    vec1 = res[0]

    h = 0
    for idx,monomial in enumerate(monomials):
        h += (vec1[idx] // monomial(*([R]*m))) * monomial
    h = h.change_ring(ZZ)
    res1 = h.monic().roots()

    if(res1 != []):
        print(ii,res1)

lists = [i for i in range(2^5)] #爆破参数，因为已知r是248bits，得到243bits，还要爆破5位
with Pool(64) as pool:
    r = list(pool.imap(attack, lists[::-1]))

然后\(r=ii*(2**rho)+res\)即可。

hint ≡ r mod p，所以 p 是 hint - r 的一个因子。可以用gcd解决，然后就是最简单的rsa解法。

三：例题

H&NCTF2025Ez-factor

题目：

from Crypto.Util.number import *
import uuid

rbits = 248
Nbits = 1024

p = getPrime(Nbits // 2)
q = getPrime(Nbits // 2)
N = p * q
r = getPrime(rbits)
hint = getPrime(Nbits // 2) * p + r
R = 2^rbits
e=0x10001
n=p*q
phi=(p-1)*(q-1)
flag = b'H&NCTF{' + str(uuid.uuid4()).encode() + b'}'
m=bytes_to_long(flag)
c=pow(m,e,n)
print("N=",N)
print("hint=",hint)
print(c)
N= 155296910351777777627285876776027672037304214686081903889658107735147953235249881743173605221986234177656859035013052546413190754332500394269777193023877978003355429490308124928931570682439681040003000706677272854316717486111569389104048561440718904998206734429111757045421158512642953817797000794436498517023
hint= 128897771799394706729823046048701824275008016021807110909858536932196768365642942957519868584739269771824527061163774807292614556912712491005558619713483097387272219068456556103195796986984219731534200739471016634325466080225824620962675943991114643524066815621081841013085256358885072412548162291376467189508
c=32491252910483344435013657252642812908631157928805388324401451221153787566144288668394161348411375877874802225033713208225889209706188963141818204000519335320453645771183991984871397145401449116355563131852618397832704991151874545202796217273448326885185155844071725702118012339804747838515195046843936285308

这道题我在H&NCTF2025 haN个人wp（密码有全解） - Mirai_haN - 博客园

这篇博客里用的参数是t=20,k=10，这里调整一下参数看看怎么个事。我调整的参数

\(t, k = 22, 11，start_bit = 200，end_bit = 248，step = 5\)

显示240成功，245失败，直接缩小距离：

from Crypto.Util.number import getPrime
from sage.all import *
from tqdm import tqdm

Nbits = 1024
p = getPrime(Nbits // 2)
q = getPrime(Nbits // 2)
N = p * q

A = getPrime(Nbits // 2)

start_bit = 240
end_bit = 248
step = 1

print("Coppersmith 小根恢复实验")
print("-" * 60)
for rbit in tqdm(range(start_bit, end_bit + 1, step), desc="正在测试 rbit 位数", unit="bit"):
    r = getPrime(rbit)
    hint = A * p + r

    R = 2^rbit
    x = ZZ['x'].gens()[0]
    f = hint - x  # f(x) = hint - x

    t, k = 22, 11
    polynomials = []
    monomials = set()

    for i in range(t + 1):
        poly = (f)^i * N^max(k - i, 0)
        polynomials.append(poly)
        monomials.update(poly.monomials())

    monomials = sorted(list(monomials), key=lambda m: m.degree())
    L = Matrix(ZZ, len(polynomials), len(monomials))

    for i, poly in enumerate(polynomials):
        for j, m in enumerate(monomials):
            L[i, j] = poly.monomial_coefficient(m) * (R^m.degree())

    try:
        L_red = L.LLL()
    except:
        tqdm.write(f"[!] LLL failed at rbit = {rbit}")
        continue

    h = 0
    for j, m in enumerate(monomials):
        h += (L_red[0][j] // (R^m.degree())) * m

    try:
        h = h.change_ring(QQ).monic()
        roots = h.roots()
    except:
        tqdm.write(f"[!] Monic or roots() failed at rbit = {rbit}")
        continue

    if roots:
        tqdm.write(f"[√] Success at rbit = {rbit:3d} | recovered r = {int(roots[0][0])}")
    else:
        tqdm.write(f"[×] Fail    at rbit = {rbit:3d} → 后续终止")
        break

得到：

正在测试 rbit 位数:  67%|██████▋   | 6/9 [00:41<00:20,  6.88s/bit]      
[√] Success at rbit = 245 | recovered r = 32864327473780248680062751134399456579500016622695289896516862433859499561
正在测试 rbit 位数:  67%|██████▋   | 6/9 [00:48<00:24,  8.03s/bit]      
[×] Fail    at rbit = 246 → 后续终止

说明最多能规约出245bits，这里建议减1，怕有误差

进行攻击：

from Crypto.Util.number import *
from tqdm import *
from itertools import *
from multiprocessing import Pool

################################################ gen data
e = 65537
N = 155296910351777777627285876776027672037304214686081903889658107735147953235249881743173605221986234177656859035013052546413190754332500394269777193023877978003355429490308124928931570682439681040003000706677272854316717486111569389104048561440718904998206734429111757045421158512642953817797000794436498517023
c = 32491252910483344435013657252642812908631157928805388324401451221153787566144288668394161348411375877874802225033713208225889209706188963141818204000519335320453645771183991984871397145401449116355563131852618397832704991151874545202796217273448326885185155844071725702118012339804747838515195046843936285308
m = 1
rho = 244
a = ["pad"] + [128897771799394706729823046048701824275008016021807110909858536932196768365642942957519868584739269771824527061163774807292614556912712491005558619713483097387272219068456556103195796986984219731534200739471016634325466080225824620962675943991114643524066815621081841013085256358885072412548162291376467189508]


def attack(ii):
    a = ["pad"] + [128897771799394706729823046048701824275008016021807110909858536932196768365642942957519868584739269771824527061163774807292614556912712491005558619713483097387272219068456556103195796986984219731534200739471016634325466080225824620962675943991114643524066815621081841013085256358885072412548162291376467189508 - 2^244*ii]

    ################################################ params
    t,k = 22,11
    R = 2^rho
    indices = []
    for i in product([i for i in range(t+1)] , repeat=m):
        if(sum(list(i)) <= t):
            indices.append(["pad"] + list(i))


    ################################################ attack
    PR = ZZ[tuple(f"X{i}" for i in range(m))]
    X = ["pad"] + list(PR.gens())
    poly = []
    monomials=set()
    for i in indices:
        f = 1
        for ij in range(1,len(i)):
            f *= (X[ij] - a[ij])^i[ij]
        l = max(k-sum(i[1:]),0)
        f *= N^l
        poly.append(f)
        for mono in f.monomials():
            monomials.add(mono)


    ################################################# LLL and resultant to find roots
    L = Matrix(ZZ,len(poly),len(monomials))
    monomials = sorted(monomials)
    for row,shift in enumerate(poly):
        for col,monomial in enumerate(monomials):
            L[row,col] = shift.monomial_coefficient(monomial)*monomial(*([R]*m))


    res = L.LLL()
    vec1 = res[0]

    h = 0
    for idx,monomial in enumerate(monomials):
        h += (vec1[idx] // monomial(*([R]*m))) * monomial
    h = h.change_ring(ZZ)
    res1 = h.monic().roots()

    if res1 != []:
        for item in res1:
            res = item[0]  
            r = ii * 2^rho + res
            print(f"{ii}, {item}, \n r={r}") 

lists = [i for i in range(2^4)]
with Pool(64) as pool:
    r = list(pool.imap(attack, lists[::-1]))

得到：r=310384729555967603261671853388867753979360895944109353196595111340924855459

解简单的rsa：

import gmpy2
from Crypto.Util.number import long_to_bytes
N= 155296910351777777627285876776027672037304214686081903889658107735147953235249881743173605221986234177656859035013052546413190754332500394269777193023877978003355429490308124928931570682439681040003000706677272854316717486111569389104048561440718904998206734429111757045421158512642953817797000794436498517023
hint= 128897771799394706729823046048701824275008016021807110909858536932196768365642942957519868584739269771824527061163774807292614556912712491005558619713483097387272219068456556103195796986984219731534200739471016634325466080225824620962675943991114643524066815621081841013085256358885072412548162291376467189508
c=32491252910483344435013657252642812908631157928805388324401451221153787566144288668394161348411375877874802225033713208225889209706188963141818204000519335320453645771183991984871397145401449116355563131852618397832704991151874545202796217273448326885185155844071725702118012339804747838515195046843936285308
r=310384729555967603261671853388867753979360895944109353196595111340924855459
p=gmpy2.gcd(hint-r,N)
q=N//p
e=65537
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,N)
print(long_to_bytes(m))
#b'H&NCTF{ac354aae-cb6b-4bd1-a9cd-090812b8f93e}'
H&NCTF2025 Ez-factor-pro

就看看怎么得到r的吧，后面sm4 ai也能解

题目：

from Crypto.Util.number import *
from Crypto.Util.Padding import *
from gmssl.sm4 import CryptSM4, SM4_ENCRYPT
from hashlib import sha256
from random import *
import uuid
rbits = 252
Nbits = 1024

p = getPrime(Nbits//2)
q = getPrime(Nbits//2)
N = p*q
r = getPrime(rbits)
hint = getPrime(Nbits// 2)*p+r
R = 2^rbits
flag = b'H&NCTF{'+str(uuid.uuid4()).encode()+b'}'
leak=p*q*r
r_bytes = long_to_bytes(leak)
iv = r_bytes[:16] if len(r_bytes) >= 16 else r_bytes + b'\0'*(16-len(r_bytes))
key = sha256(str(p + q + r).encode()).digest()[:16] 
crypt_sm4 = CryptSM4()
crypt_sm4.set_key(key, SM4_ENCRYPT)
padded_flag = pad(flag, 16)
c = crypt_sm4.crypt_cbc(iv, padded_flag)
print("N=",N)
print("hint=",hint)
print(c)
#N = 133196604547992363575584257705624404667968600447626367604523982016247386106677898877957513177151872429736948168642977575860754686097638795690422242542292618145151312000412007125887631130667228632902437183933840195380816196093162319293698836053406176957297330716990340998802156803899579713165154526610395279999
#hint = 88154421894117450591552142051149160480833170266148800195422578353703847455418496231944089437130332162458102290491849331143073163240148813116171275432632366729218612063176137204570648617681911344674042091585091104687596255488609263266272373788618920171331355912434290259151350333219719321509782517693267379786
#c = 476922b694c764725338cca99d99c7471ec448d6bf60de797eb7cc6e71253221035eb577075f9658ac7f1a40747778ac261787baad21ee567256872fa9400c37

用测试代码看参数

from Crypto.Util.number import getPrime
from sage.all import *
from tqdm import tqdm

Nbits = 1024
p = getPrime(Nbits // 2)
q = getPrime(Nbits // 2)
N = p * q

A = getPrime(Nbits // 2)

start_bit = 240
end_bit = 252
step = 1

print("Coppersmith 小根恢复实验")
print("-" * 60)
for rbit in tqdm(range(start_bit, end_bit + 1, step), desc="正在测试 rbit 位数", unit="bit"):
    r = getPrime(rbit)
    hint = A * p + r

    R = 2^rbit
    x = ZZ['x'].gens()[0]
    f = hint - x  # f(x) = hint - x

    t, k = 27,13
    polynomials = []
    monomials = set()

    for i in range(t + 1):
        poly = (f)^i * N^max(k - i, 0)
        polynomials.append(poly)
        monomials.update(poly.monomials())

    monomials = sorted(list(monomials), key=lambda m: m.degree())
    L = Matrix(ZZ, len(polynomials), len(monomials))

    for i, poly in enumerate(polynomials):
        for j, m in enumerate(monomials):
            L[i, j] = poly.monomial_coefficient(m) * (R^m.degree())

    try:
        L_red = L.LLL()
    except:
        tqdm.write(f"[!] LLL failed at rbit = {rbit}")
        continue

    h = 0
    for j, m in enumerate(monomials):
        h += (L_red[0][j] // (R^m.degree())) * m

    try:
        h = h.change_ring(QQ).monic()
        roots = h.roots()
    except:
        tqdm.write(f"[!] Monic or roots() failed at rbit = {rbit}")
        continue

    if roots:
        tqdm.write(f"[√] Success at rbit = {rbit:3d} | recovered r = {int(roots[0][0])}")
    else:
        tqdm.write(f"[×] Fail    at rbit = {rbit:3d} → 后续终止")
        break

得到：

正在测试 rbit 位数:  54%|█████▍    | 7/13 [02:33<02:34, 25.71s/bit]      
[√] Success at rbit = 246 | recovered r = 103481985767264517426495113854780189210799617812947619990557524067534720921
正在测试 rbit 位数:  54%|█████▍    | 7/13 [03:15<02:47, 27.92s/bit]      
[×] Fail    at rbit = 247 → 后续终止

用t, k = 27,13，rho=245来攻击：

from Crypto.Util.number import *
from tqdm import *
from itertools import *
from multiprocessing import Pool

################################################ gen data
e = 65537
N = 133196604547992363575584257705624404667968600447626367604523982016247386106677898877957513177151872429736948168642977575860754686097638795690422242542292618145151312000412007125887631130667228632902437183933840195380816196093162319293698836053406176957297330716990340998802156803899579713165154526610395279999
hint = 88154421894117450591552142051149160480833170266148800195422578353703847455418496231944089437130332162458102290491849331143073163240148813116171275432632366729218612063176137204570648617681911344674042091585091104687596255488609263266272373788618920171331355912434290259151350333219719321509782517693267379786
m = 1
rho = 245
a = ["pad"] + [hint]


def attack(ii):
    a = ["pad"] + [hint - 2^245*ii]

    ################################################ params
    t,k = 27,13
    R = 2^rho
    indices = []
    for i in product([i for i in range(t+1)] , repeat=m):
        if(sum(list(i)) <= t):
            indices.append(["pad"] + list(i))


    ################################################ attack
    PR = ZZ[tuple(f"X{i}" for i in range(m))]
    X = ["pad"] + list(PR.gens())
    poly = []
    monomials=set()
    for i in indices:
        f = 1
        for ij in range(1,len(i)):
            f *= (X[ij] - a[ij])^i[ij]
        l = max(k-sum(i[1:]),0)
        f *= N^l
        poly.append(f)
        for mono in f.monomials():
            monomials.add(mono)


    ################################################# LLL and resultant to find roots
    L = Matrix(ZZ,len(poly),len(monomials))
    monomials = sorted(monomials)
    for row,shift in enumerate(poly):
        for col,monomial in enumerate(monomials):
            L[row,col] = shift.monomial_coefficient(monomial)*monomial(*([R]*m))


    res = L.LLL()
    vec1 = res[0]

    h = 0
    for idx,monomial in enumerate(monomials):
        h += (vec1[idx] // monomial(*([R]*m))) * monomial
    h = h.change_ring(ZZ)
    res1 = h.monic().roots()

    if res1 != []:
        for item in res1:
            res = item[0]  
            r = ii * 2^rho + res
            print(f"{ii}, {item}, \n r={r}") 

lists = [i for i in range(2^7)]
with Pool(64) as pool:
    r = list(pool.imap(attack, lists[::-1]))

得到

126, (42423940599061053472159969219266251718242090735467449446125954222952455085, 1), 
 r=7166351305785506670352015492214713707534657162937963088592442157834795391917
127, (-14115165473847245074505550804507140788237393964552357213765444218411377747, 1), 
 r=7166351305785506670352015492214713707534657162937963088592442157834795391917

那么\(p=gmpy2.gcd(hint-r,N)\)

结束战斗

四：丢番图近似 SDA 格攻击

参考AGCD近似最大公约数问题 | 独奏の小屋

\(xl=p*ql+rl\)

image-20210903140354348

对于上述问题，我们需要描述得更精确些，其中 \(p\) 的大小为 \(\eta\) 位，\(r_i\) 的大小为 \(\rho\) 位（包含正负），而 \(q_i\) 的大小为 \(\gamma - \eta\) 位（即 \(x\) 的大小为 \(\gamma\) 位 ）。这类题目会给很多组x，虽然最少两组就能构造格，但是肯定是越多成功率越高

ACD 所需参数为 \((\gamma, \eta, \rho)\)。

以 \((x_0, x_1)\) 对为例，我们考虑

\[\begin{align} q_0x_1 - q_1x_0 &= q_0(q_1p + r_1) - q_1(q_0p + r_0) \tag{4} \\ &= q_0q_1p + q_0r_1 - q_1q_0p - q_1r_0 \tag{5} \\ &= q_0r_1 - q_1r_0 \tag{6} \end{align} \]

对于 \(l - 1\) 组，我们可以构建方程组

\[(q_0, q_1, \cdots, q_l) \begin{bmatrix} 2^{\rho + 1} & x_1 & x_2 & \cdots & x_l \\ & -x_0 & & & \\ & & -x_0 & & \\ & & & \ddots & \\ & & & & -x_0 \end{bmatrix} = (q_02^{\rho + 1}, q_0r_1 - q_1r_0, \cdots, q_0r_l - q_lr_0) \tag{7} \]

可以证明的是，解向量是格中的短向量。

生成代码：

from Crypto.Util.number import getPrime, getRandomRange

def gen(k:int, gamma: int, eta: int, rho: int):
    xs = []
    qs = []
    rs = []
    p = getPrime(eta)
    for _ in range(k):
        q = getPrime(gamma - eta)
        r = getRandomRange(-pow(2, rho) + 1, pow(2, rho) - 1)
        qs.append(q)
        rs.append(r)
        xs.append(p * q + r)
    return p, qs, rs, xs

k = 5   #个数
eta = 768  #p大小 
gamma = 1024 + eta #x大小
rho = 256 #r大小
#q的大小为 gamma - eta
p, qs, rs, xs = gen(k, gamma, eta, rho)
print("p =", p)
print("qs =", qs)
print("rs =", rs)
print("xs =", xs)

解密代码：

k = 5
rho = 256
xs = []


M = matrix(ZZ, k, k)
M[0, 0] = 2^(rho + 1)
for j in range(1, k):
    M[0, j] = xs[j]  
for i in range(1, k):
    M[i, i] = -xs[0]  
L = M.LLL()
q0 = ZZ(L[0, 0] / M[0, 0]).abs()
r = ZZ(xs[0] % q0)
r0 = r if r <= 2**rho else r - q0
p = ZZ((xs[0] - r0) / q0)
print("r0 =", r0)
print("q0 =", q0)
print("p =", p)

改了一下代码，原博客的生成方式是e0 = ZZ(xs[0] % q0)，但是%运算返回的是正值，如果r0的真实值是负值那么会导致r0算错接着导致p错误。
证明：

\(x_s[0] = p \times q_0 + r_0\)

\(x_s[0] = (p-1) \times q_0 + (q_0 + r_0)\)

\(p \times q_0 + r_0 = (p-1) \times q_0 + q_0 + r_0\)

\(x_s[0] \mod q_0 = (q_0 + r_0) \mod q_0 = q_0 + r_0\)

  • 因为 |r_0| < q_0，所以 q_0 - |r_0| > 0
  • 又因为 |r_0| > 0，所以 q_0 - |r_0| < q_0
  • 综上：0 < q_0 + r_0 < q_0

攻击条件：

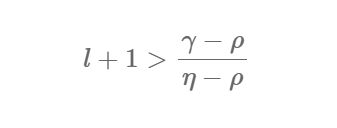
五：正交格近似 OL 格攻击

暂时不会，慢慢研究把

菜鸟一枚，要是有错误欢迎各路大佬指正

posted @ 2025-06-22 15:35  Mirai_haN  阅读(321)  评论(0)    收藏  举报