【清华集训2014】主旋律

https://i.cnblogs.com/EditPosts.aspx?opt=1

https://blog.csdn.net/qq_39972971/article/details/79386886#commentBox

删掉一些边强连通——>保留一些边不强连通

也就是，缩点之后变成DAG（且>1个点)

简化一下，考虑s这个导出子图，选择一个边集是DAG的方案数。

经典问题，枚举入度为0的点，然后容斥

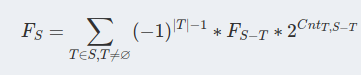
对于强连通呢？

可以直接枚举缩点的情况，复杂度不可估量。

发现，对于T，系数只和T的奇偶性有关，所以我们不需要知道T内部划分，只要知道T被划分成了几个SCC

所以

F(s)表示s这个导出子图的是强连通的边集数量。G(s),H(s)分别表示，s这个集合划分成奇数、偶数个SCC的方案数且任意两个SCC之间没有边。

转移：

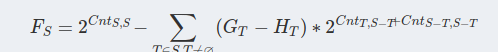
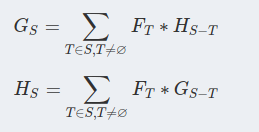
第一个的T=S时候，G（S）不能包含S本身是一个SCC的情况

所以先不枚举T=S，最后再处理。

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Modulo{
const int mod=1e9+7;
il int ad(int x,int y){return x+y>=mod?x+y-mod:x+y;}
il int sub(int x,int y){return ad(x,mod-y);}
il int mul(int x,int y){return (ll)x*y%mod;}
il void inc(int &x,int y){x=ad(x,y);}
il void inc2(int &x,int y){x=mul(x,y);}
il int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;}
template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);}
template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);}
}
using namespace Modulo;
namespace Miracle{
const int N=15;
const int M=266;
int n,m;
bitset<M>in[1<<N],out[1<<N];
int f[1<<N],g[1<<N],h[1<<N];
int mi[M];
int cnt(int s,int t){return (out[s]&in[t]).count();}
int main(){
    rd(n);rd(m);
    mi[0]=1;
    for(reg i=1;i<=m;++i) mi[i]=mul(mi[i-1],2);
    int x,y;
    for(reg i=1;i<=m;++i){
        rd(x);rd(y);
        --x;--y;
        for(reg s=0;s<(1<<n);++s){
            if((s>>x)&1) out[s].set(i);
            if((s>>y)&1) in[s].set(i); 
        }
    }
    h[0]=1;g[0]=0;f[0]=1;
    for(reg s=1;s<(1<<n);++s){
        f[s]=mi[cnt(s,s)];
        int lo=s&(-s);
        for(reg t=(s-1)&s;t;t=(t-1)&s){
            inc(f[s],mod-mul(sub(g[t],h[t]),mi[cnt(t,s-t)],mi[cnt(s-t,s-t)]));
            
            if(!(t&lo)) continue;
            inc(g[s],mul(f[t],h[s-t]));
            inc(h[s],mul(f[t],g[s-t]));
        }
        inc(f[s],mod-sub(g[s],h[s]));
        inc(g[s],mul(f[s],h[0]));
        inc(h[s],mul(f[s],g[0]));
    }
    cout<<f[(1<<n)-1];
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
*/