51nod1584 加权约数和
枚举较大的作为i,干掉max,乘2,再减去i=j的部分

第一个方向,就是处理
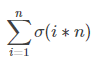
然后大力反演一波
大致思路就是把miu(d)往前提,变成枚举n的约数的形式
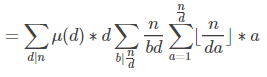
虽然这个玩意根本看不出来有什么可以算下去的理由。。。
带回去:各种交换求和号,把后面的sigma变成可以提前预处理的东西

已经可以做到O(nlogn)预处理O(sqrt(n))询问,(感觉题目就是这样的复杂度吧。。。)
可以做到更好:
枚举d,i的上限是n/d
不如直接枚举i*d
然后变成枚举约数形式!(往往这里是化简的关键!因为枚举约数的形式可以O(nlogn)暴力预处理)

F是积性函数
要支持快速计算p^k才能线性筛
但是当n是p^k形式好像不太能快速计算?反正约数就k+1个,可以暴力计算
可以直接计算,因为有miu(d)一项,所以只有1,p两项有值
手动算一下即可。
O(n)预处理+O(1)查询
反正我懒,直接枚举约数
upda:以上在fp,因为ssumd不是积性函数,F并不是积性函数
O(nlogn)预处理+O(1)查询
至于

直接同理代换sigma(i^2),然后莫比乌斯反演,d提到i的后面去。
预处理一些东西即可。
总复杂度:O(n)+O(T)
总复杂度:O(nlogn)+O(T)
Code:O(nlogn)预处理的代码:
#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Modulo{ const int mod=1e9+7; int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;} void inc(int &x,int y){x=ad(x,y);} int mul(int x,int y){return (ll)x*y%mod;} void inc2(int &x,int y){x=mul(x,y);} int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);} template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);} } using namespace Modulo; namespace Miracle{ const int N=1e6+5; int pri[N],tot; int vis[N]; int s[N],d[N],mu[N],mdiv[N]; int iv[N]; int h[N],g[N]; int f[N]; void sieve(int n){ mu[1]=1;d[1]=1; for(reg i=2;i<=n;++i){ if(!vis[i]){ pri[++tot]=i; mu[i]=mod-1;mdiv[i]=1+i; d[i]=1+i; } for(reg j=1;j<=tot;++j){ if(i*pri[j]>n) break; vis[i*pri[j]]=1; int to=i*pri[j]; if(i%pri[j]==0){ mu[to]=0; d[to]=d[i]/mdiv[i]*(mdiv[i]*pri[j]+1); mdiv[to]=mdiv[i]*pri[j]+1; break; } mu[to]=mod-mu[i]; d[to]=d[i]*d[pri[j]]; mdiv[to]=mdiv[pri[j]]; } } iv[1]=1; for(reg i=1;i<=n;++i){ s[i]=ad(s[i-1],d[i]); if(i!=1) iv[i]=mul(mod-mod/i,iv[mod%i]); } for(reg i=1;i<=n;++i){ for(reg j=i;j<=n;j+=i){ f[j]=ad(f[j],mul(mu[i],i,j,s[j/i],d[j/i])); h[j]=ad(h[j],iv[i]); } } for(reg i=1;i<=n;++i){ inc(f[i],f[i-1]); h[i]=mul(h[i],d[i]); } for(reg i=1;i<=n;++i){ for(reg j=i;j<=n;j+=i){ g[j]=ad(g[j],mul(mu[i],h[j/i])); } } for(reg i=1;i<=n;++i){ g[i]=mul(g[i],i,i); g[i]=ad(g[i],g[i-1]); } } int main(){ sieve(N-4);int t; rd(t);int x; int o=0; while(t--){ rd(x);++o; int ans=ad(mul(2,f[x]),mod-g[x]); printf("Case #%d: %d\n",o,ans); } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
推式子好题
其实就几个套路:
0.sigma(i*j)的转化
1.分成一个个部分逐一击破
2.莫比乌斯反演
3.把miu(d)往前提,尽量变成枚举约数的形式,易于预处理后面一些东西,加上miu(d),可以线性筛、整除分块、枚举约数来处理
4.枚举T=i*d


 浙公网安备 33010602011771号
浙公网安备 33010602011771号