sequence——强行推式子+组合意义


考虑长度<=x的方案数F(x),然后(F(x)-F(x-1))*x贡献到答案里
n平方的做法可以直接DP,
感觉有式子可言,
就推出式子:类似coat,每个长度为i的计算i次。
再容斥下:
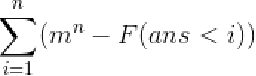
F是方案数,还是求:
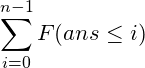
枚举分成的段数,枚举多少个超过i进行容斥:
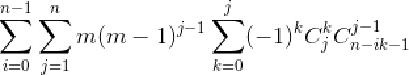
突破口:有个n-i*k-1,意味着i*k<=n,这样的i和k暴力枚举一共nlogn复杂度!
提出来,考虑干掉j
强行推式子:
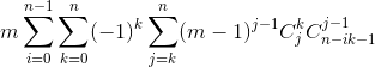

处理:
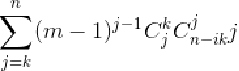
(怎么看怎么也看不出什么道理的样子)
来找组合意义吧:
有n-ik个球,我们先从中选出j个,再从选出的j个中选出k个。在j个球中我们选出一个特殊的球,对于剩下的球用m-1种颜色染色。
考虑讨论这个特殊的球是不是这k个球中的
即可得到;
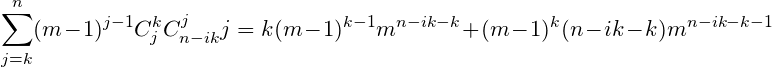 (这里少写了C(n-i*k-k,k))
(这里少写了C(n-i*k-k,k))
预处理m-1的次幂和m的次幂和阶乘阶乘逆元
O(nlogn)
别忘了最后用n*m^n-
#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} int mod; namespace Modulo{ int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;} void inc(int &x,int y){x=ad(x,y);} int mul(int x,int y){return (ll)x*y%mod;} void inc2(int &x,int y){x=mul(x,y);} int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} } using namespace Modulo; namespace Miracle{ const int N=300000+5; int n,m; int jie[N],inv[N]; int iv[N]; int m0[N],m1[N]; int C(int n,int m){ if(n<0||m<0||n<m) return 0; return mul(jie[n],mul(inv[m],inv[n-m])); } int main(){ rd(n);rd(m);rd(mod); jie[0]=1; for(reg i=1;i<=n;++i) jie[i]=mul(jie[i-1],i); inv[n]=qm(jie[n],mod-2); for(reg i=n-1;i>=0;--i) inv[i]=mul(inv[i+1],i+1); iv[1]=1; for(reg i=2;i<=n;++i){ iv[i]=mul(mod-mod/i,iv[mod%i]); } m0[0]=m1[0]=1; for(reg i=1;i<=n;++i){ m0[i]=mul(m0[i-1],m); m1[i]=mul(m1[i-1],m-1); } int ans=0; for(reg i=0;i<n;++i){ for(reg k=0;k<=n;++k){ if(i*k+k>n) break; int tmp=0;// if(k!=0) tmp=ad(tmp,mul(C(n-i*k,k),mul(k,mul(m1[k-1],m0[n-i*k-k])))); if(n-i*k-k-1>=0) tmp=ad(tmp,mul(C(n-i*k,k),mul(m1[k],mul(m0[n-i*k-k-1],n-i*k-k)))); tmp=mul(tmp,(k&1)?mod-1:1); tmp=mul(tmp,iv[n-i*k]); ans=ad(ans,tmp); } } ans=mul(ans,m); ans=ad(mul(n,qm(m,n)),mod-ans); ot(ans); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
突破口是i,k总共对数nlogn级别,干掉j用组合意义大力推导


 浙公网安备 33010602011771号
浙公网安备 33010602011771号