[题集]计算几何
1

n<=500
法一:随机化最大团
法二:
每个蜘蛛是一个三维直线(x,y,t)
考虑按照所属面分别考虑这些蜘蛛
一些个蜘蛛相交,当且仅当这些直线共面
还有一种蜘蛛交在一点的情况,先判掉:
枚举两个直线,确定平面
枚举剩下的直线,考虑是否有交点
先考虑是否有所有直线交在一点
然后平行的只保留一个
再考虑共面
如果之前有三直线不共点:直接查是不是在平面上
否则如果和第一第二条直线交点重合,先留着,最后和某一个交点不重合的进行判断是否共面
2
给出一个点集
• 你要选择一个子集,其中每个点有 pi 的概率在子集中
• 求凸包面积的期望
𝑛 ≤ 10^3
凸包的面积计算可以独立
考虑每个边在所有凸包上出现的贡献
带方向枚举每条边,这条边存在当且仅当右侧没有点并且两个端点存在
每次级角排序+扫描线即可
3
你有 𝑛 个点
• 求最多能选出多少个其中的点,使得这些点两两之间的连线不和
以原点为圆心 𝑟 为半径的圆相交
𝑛 ≤ 2000
https://www.lydsy.com/JudgeOnline/problem.php?id=4660
其实,就是这些点和圆的两个切线之间的圆弧有关系,设圆弧为si
则这个集合的两两圆弧必须相交并且不互相包含
枚举第一个圆弧是哪个,剩下可选择的圆弧按照左端点排序,右端点必然是上升的,所以对右端点求LIS即可
挺巧的
4
平面上有很多蓝点和红点
你需要求一个最大的蓝点为顶点的凸多边形,要求其边界和内部都不能
出现红点
n<=100
bzoj3778共鸣
类似THUWC2019 D2T3
考虑枚举左下角,f[i][j]最后一个是j,倒数第二个是i,O(n^3)
发现枚举下一个的时候,就是多了一个三角形,所以预处理这个三角形内部有没有红点即可
预处理方法:
法一:O(n^3)
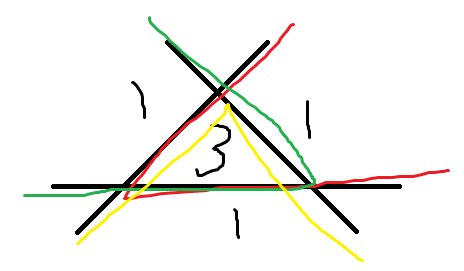
把三个角内部的红色点都加上,黑色是该区域红点计算次数
这个可以预处理以每个点的级角序排序结果+双指针:O(n^3)预处理
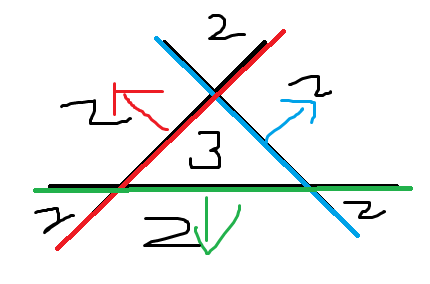
每个线段箭头方向的红点数量也加上
然后减去所有红点个数的2倍
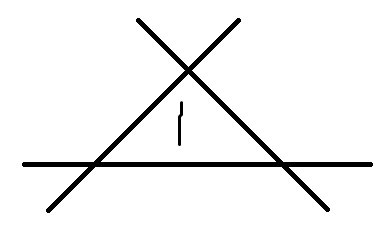
就是最后的答案了!
法二:不完全O(n^4)
枚举右下角的点s,把涉及到的点放进数组
级角序排序
顺序枚举两个点i,j和s形成三角形,同时用指针维护可能出现在三角形的红点编号区间[be+1,ptr]
暴力在这个区间看是否有红点在三角形中
只要随便判断叉积是否为负什么的即可

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Modulo{ const int mod=998244353; int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;} void inc(int &x,int y){x=ad(x,y);} int mul(int x,int y){return (ll)x*y%mod;} void inc2(int &x,int y){x=mul(x,y);} int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} } //using namespace Modulo; namespace Miracle{ const int N=105; const int inf=0x3f3f3f3f; int n,m; struct po{ int x,y; po(){} po(int xx,int yy){x=xx;y=yy;} po friend operator +(po a,po b){ return po(a.x+b.x,a.y+b.y); } po friend operator -(po a,po b){ return po(a.x-b.x,a.y-b.y); } int friend operator *(po a,po b){ return a.x*b.y-a.y*b.x; } }a[N],b[N],st[N],no[N],std; int ca,cb; bool smal(po a,po b){ return atan2(a.y-std.y,a.x-std.x)<atan2(b.y-std.y,b.x-std.x); } bool cmp(po a,po b){ double d1=atan2(a.y-std.y,a.x-std.x),d2=atan2(b.y-std.y,b.x-std.x); if(d1!=d2) return d1<d2; return max(a.x,a.y)<max(b.x,b.y); } int f[N][N],ok[N][N]; int ans; void sol(int now){ ca=cb=0; for(reg i=1;i<=n;++i){ if(i==now) continue; if(a[i].x>std.x||(a[i].x==std.x&&a[i].y>=std.y)) st[++ca]=a[i]; } for(reg i=1;i<=m;++i){ if(b[i].x>std.x||(b[i].x==std.x&&b[i].y>=std.y)) no[++cb]=b[i]; } sort(st+1,st+ca+1,cmp);sort(no+1,no+cb+1,cmp); for(reg i=1;i<=ca;++i){ int be=0; while(be<cb&&smal(no[be+1],st[i])) ++be; int ptr=be; for(reg j=i+1;j<=ca;++j){ ok[i][j]=0; while(ptr<cb&&!smal(st[j],no[ptr+1])) ++ptr; for(reg k=be+1;k<=ptr;++k){ int sz=(st[i]-no[k])*(st[j]-no[k]); if(sz>=0){ ok[i][j]=-1; } } } } memset(f,-inf,sizeof f); for(reg i=1;i<=ca;++i){ for(reg j=i+1;j<=ca;++j){ if(ok[i][j]!=-1){ f[i][j]=max(f[i][j],(st[i]-std)*(st[j]-std)); } for(reg k=j+1;k<=ca;++k){ if(ok[j][k]!=-1&&(st[j]-st[i])*(st[k]-st[i])>=0){ f[j][k]=max(f[j][k],f[i][j]+(st[j]-std)*(st[k]-std)); } } ans=max(ans,f[i][j]); } } } int main(){ rd(n);rd(m); for(reg i=1;i<=n;++i) rd(a[i].x),rd(a[i].y); for(reg i=1;i<=m;++i) rd(b[i].x),rd(b[i].y); for(reg i=1;i<=n;++i){ std=a[i]; sol(i); } printf("%.2lf",(double)ans/2.0); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
5
平面上有 𝑛 个圆
你需要从一个起点到一个终点
每次,如果你在其中一个圆内,你可以把自己绕圆心旋转一个角度
问能不能在有限步内走到
n<=50

求交点,暴力BFS
6
给一个格点凸多边形,两个人轮流操作
每次操作需要画一个格点凸多边形(面积不能是 0),满足该多
边形的顶点在上一个多边形的内部或边界上,但不能和上一个多
边形的顶点重合
求是先手必胜还是后手必胜
𝑛 ≤ 100, |𝑥|, |𝑦| ≤ 10^5
伪博弈题
只要凸多边形内部有一个三角形,那么先手就必胜了
枚举横坐标,考虑这个横坐标这一列有多少个点(枚举n个外边界,卡出边界即可)
如果存在>=2个有点,存在一个>=2个,先手必胜
否则一定都共线,先手必败



 浙公网安备 33010602011771号
浙公网安备 33010602011771号