【学习笔记】反射容斥
基本公式
最平凡
考虑平凡的网格图计数,从 \((0,0)\) 往右或往上走,走到 \((n,m)\) 方案数为 \(\binom{n+m}{n}\)。
较平凡
若不经过直线 \(y = x+b\),直接在第一次经过这个直线的地方翻折,如下图。
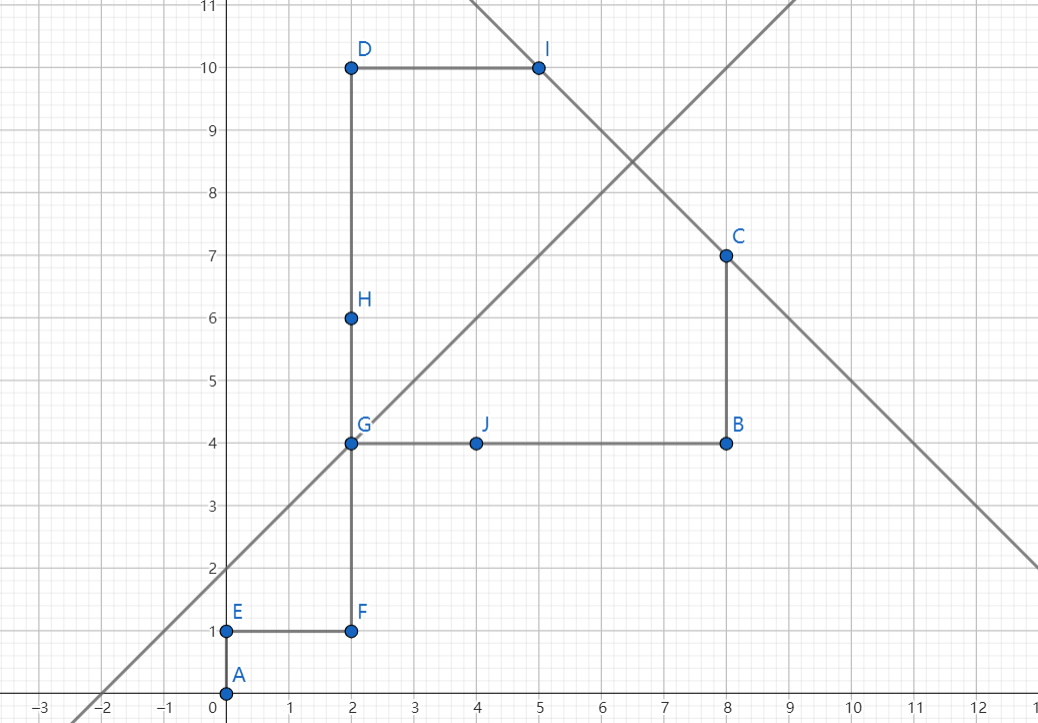
\(A\to G\to C\) 翻转成 \(A \to G \to I\),这些都是一一对应的。
方案就减去 \((0,0)\to (m-b,n+b)\) 的方案数 \(\binom{n+m}{n}-\binom{m+n}{m-b}\)。
平凡
考虑不经过 \(y=x+b,y=x+c\) 两条直线,设两条直线为 \(B,C\)。
把一条路径表示为依次穿过的路径,如 \(BBCCB\),考虑到多次穿过一条直线只用保留一条,就变成 \(BCBCBC,CBCBCB\)。
直接开始容斥,\(ans=\empty -B-C+BC+CB-BCB-CBC+BCBC+CBCB...\)。
可以分为 \(BCBC\) 和 \(CBCB\) 统计,每次穿过一条直线把目标点关于这条直线对称即可。
复杂度 \(\Theta(\dfrac{n+m}{|b-c|})\)。
例题
P3266
考虑每行 \(a_{i,j}<a_{i,j+1}\),且 \(a_{i,j} \in [0,m],j\in [1,m]\),所以每行中有且仅有一个 \([0,m]\) 的数不出现。
\(f_{i,j}\) 第 \(i\) 行 \(j\) 不出现方案数。
\(f_{i,j} = \sum\limits_{k=0}^{j+1} f_{i-1,k}\)
等价于 \(f_{i,j}=f_{i,j-1}+f_{i-1,j+1}\),答案为 \(f_{n+1,m}\)。
组合意义是从 \((1,0)\) 出发到 \((n+1,m)\),每次往右或往左上,当 \(x=1\) 时可以往上的方案数,转动 \(45\degree\),发现是从 \((0,0)\) 走到 \((n+m+1,n)\) 且不经过 \(y=x+1,y=x-m-2\) 的方案,按照上面的方法做就行。
#include <bits/stdc++.h>
#define _rep(i, x, y) for(int i = x; i <= y; ++i)
#define _req(i, x, y) for(int i = x; i >= y; --i)
#define _rev(i, u) for(int i = head[u]; i; i = e[i].nxt)
#define pb push_back
#define fi first
#define se second
#define mst(f, i) memset(f, i, sizeof f)
using namespace std;
#ifdef ONLINE_JUDGE
#define debug(...) 0
#else
#define debug(...) fprintf(stderr, __VA_ARGS__), fflush(stderr)
#endif
typedef long long ll;
typedef pair<int, int> PII;
namespace fastio{
char ibuf[50007],*p1 = ibuf, *p2 = ibuf;
#ifdef ONLINE_JUDGE
#define get() p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, 50007, stdin), p1 == p2) ? EOF : *p1++
#else
#define get() getchar()
#endif
template<typename T> inline void read(T &t){
T x = 0, f = 1;
char c = getchar();
while(!isdigit(c)){
if(c == '-') f = -f;
c = getchar();
}
while(isdigit(c)) x = x * 10 + c - '0', c = getchar();
t = x * f;
}
template<typename T, typename ... Args> inline void read(T &t, Args&... args){
read(t);
read(args...);
}
template<typename T> void write(T t){
if(t < 0) putchar('-'), t = -t;
if(t >= 10) write(t / 10);
putchar(t % 10 + '0');
}
template<typename T, typename ... Args> void write(T t, Args... args){
write(t), putchar(' '), write(args...);
}
template<typename T> void writeln(T t){
write(t);
puts("");
}
template<typename T> void writes(T t){
write(t), putchar(' ');
}
#undef get
};
using namespace fastio;
#define multitest() int T; read(T); _rep(tCase, 1, T)
namespace Calculation{
const ll mod = 1e9 + 7;
ll ksm(ll p, ll h){ll base = p % mod, res = 1; while(h){if(h & 1ll) res = res * base % mod; base = base * base % mod, h >>= 1ll;} return res;}
void dec(ll &x, ll y){x = ((x - y) % mod + mod) % mod;}
void add(ll &x, ll y){x = (x + y) % mod;}
void mul(ll &x, ll y){x = x * y % mod;}
ll sub(ll x, ll y){return ((x - y) % mod + mod) % mod;}
ll pls(ll x, ll y){return ((x + y) % mod + mod) % mod;}
ll mult(ll x, ll y){return x * y % mod;}
}
using namespace Calculation;
const int N = 4e6 + 5;
ll n, m, pw[N], inv[N];
ll C(ll n, ll m){
if(n < m || m < 0) return 0;
if(n == m || !m) return 1;
return pw[n] * inv[m] % mod * inv[n - m] % mod;
}
ll b, c, x, y;
ll calc(ll x, ll y){return C(x + y, x);}
void work(ll &x, ll &y, ll b){
ll tx = x, ty = y;
y = tx + b, x = ty - b;
}
void work(ll &b, ll &c){
b = 2 * c - b;
}
int main(){
read(n, m), pw[1] = inv[1] = 1;
_rep(i, 2, 4e6) pw[i] = pw[i - 1] * i % mod, inv[i] = (-mod / i + mod) * inv[mod % i] % mod;
_rep(i, 2, 4e6) inv[i] = inv[i - 1] * inv[i] % mod;
b = 1, c = -m - 2, x = n + m + 1, y = n;
ll ans = calc(x, y);
for(int i = 1; x >= 0 && y >= 0; ++i){
if(i & 1){
work(x, y, b), dec(ans, calc(x, y));
work(c, b);
}else{
work(x, y, c), add(ans, calc(x, y));
work(b, c);
}
}
b = 1, c = -m - 2, x = n + m + 1, y = n;
for(int i = 1; x >= 0 && y >= 0; ++i){
if(i & 1){
work(x, y, c), dec(ans, calc(x, y));
work(b, c);
}else{
work(x, y, b), add(ans, calc(x, y));
work(c, b);
}
}
writeln(ans);
return 0;
}
GYM104053J
\(4s_i=(a_i +1)^2\) 即 \(4s_{i-1} = (a_i-1)^2\),即 \(a_i = 1\pm 2\sqrt{s_{i-1}}\)。
\(s_i=s_{i-1} -2\sqrt{s_{i-1}}+1=(\sqrt{s_{i-1}} -1)^2\) 或 \(s_i = s_{i-1} + 2\sqrt{s_{i-1}}+1=(\sqrt{s_{i-1}}+1)^2\)。考虑二元组 \((i,\sqrt{s_i})\),可以走到 \((i,\sqrt{s_i}+1),(i,\sqrt{s_i}-1)\)。
同样旋转一下,又因为 \(|a_i|\le m\),所以转化为从 \((0,0)\) 出发,不经过直线 \(y=x+\dfrac{m+1}{2}+1,y=x-1\),最后终点在 \(y=-x+n\) 上的方案。
可以直接枚举终点,复杂度 \(\Theta(b-c)\),乘上容斥复杂度就是 \(\Theta(n+m)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号