算法随想Day33【贪心算法】| LC738-单调递增的数字、LC996-监控二叉树

LC738. 单调递增的数字

用queue容器辅助实现的版本

int monotoneIncreasingDigits(int n)
{
    deque<int> que;
    int temp = n;
    while (temp > 0)
    {
        que.emplace_front(temp % 10);
        temp /= 10;
    }

    int index = que.size();
    for (int i = que.size() - 1; i >= 1; --i)
    {
        if (que[i] < que[i - 1])
        {
            --que[i - 1];
            for (int j = i; j < index; ++j)
            {
                que[j] = 9;
            }
            index = i;
        }
    }

    int result = 0;
    for (int j = 0; j < que.size(); ++j)
    {
        result = 10 * result + que[j];
    }
    return result;
}

用数值本身实现的版本。这种方法在做的时候遇到一个问题，times变量会达到10^10，超出signed int的正值范围，需要把一些相关的变量/常量设置成long long型的，否则会出现如下错误情况

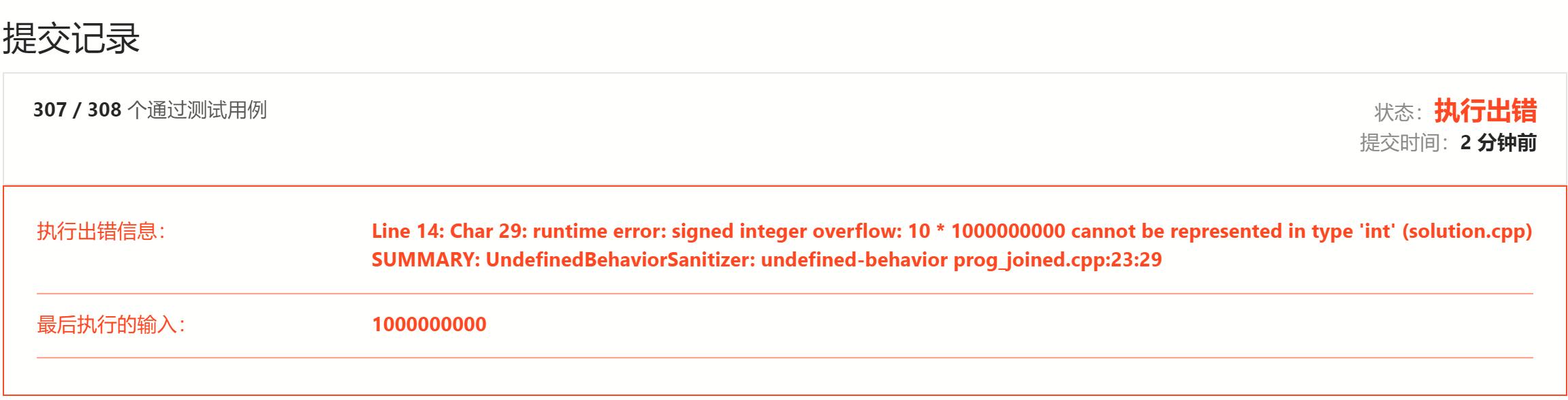
int monotoneIncreasingDigits(int n)
{
    int N_temp = n;
    long long times = 10;
    int right = N_temp % 10;
    N_temp /= 10;
    while (N_temp > 0)
    {
        int Right_temp = N_temp % 10;
        if (Right_temp > right)
        {
            long long lln = n / (10ll * times) * (10ll * times) + (Right_temp - 1) * times + (times - 1);
            n = (int)lln;
            --Right_temp;
        }
        times *= 10ll;
        right = Right_temp;
        N_temp /= 10ll;  
    }
    return n;
}

示例题解中，使用string容器辅助实现的版本：

• 省去了to_string 和 stoi 的过程，需要自己编写函数。

• 只需找出最左边开始需要填充9的位置，后面再for也统一赋"9"即可

int monotoneIncreasingDigits(int n) {
    string record = to_string(n);
    int k = record.size();
    for(int i = record.size()-1; i > 0; i--){
        if(record[i-1] > record[i]){
            k = i;
            record[i-1]--;
        }
    }
    for(int i = k; i < record.size(); i++){
        record[i] = '9';
    }
    return stoi(record);
}

LC996. 监控二叉树

开始自己琢磨的：根据节点的左右孩子状态，确定当前节点的返回值和是否需要增加摄像头，会出现问题。没有考虑到的情况，（如一条链表型树，0->0->0->0->0->0，按照开始的想法，从底向顶进行后续遍历，其实会每隔一个节点就安装一个监控，形成1->0->1->0->1->0的情况，但其实只需要0->1->0->0->1->0即可全部覆盖），就是忽略了一个贪心的前提，每个监控能够监控到其上、中、下三层，所以一旦安装了监控，其往上两层都不用安装了，即从叶子节点的角度开始节省监控。如安装了第一个监控时，即0->0->0->0->1->0，往上走，来到第三个0的地方，此时可以把它当中一个新的叶子节点，这是相对其父子节点来说的（父子节点存不存在另当别论）。

Carl哥思路：给节点设置状态

​ 0：无覆盖 1：有摄像头 2：有覆盖

空节点应该被视为“有覆盖”的状态，因为如果是“无覆盖”的话，其父子节点（对整个树来说是叶子节点）就必须得安装监控，就做不到在叶子节点中最大化地节省监控

状态转移，分类讨论：

• 叶子节点，左右孩子都为2“有覆盖”，则设置其为“无覆盖”
• 左右孩子，至少有1个为“无覆盖”，则设置其为“有摄像头”
• 左右孩子，至少有1个为“有摄像头”，则设置其为“有覆盖”
• 处于整个树的根节点，且此时为“无覆盖”，则此时需要加多一个摄像头

////开始自己写的
int count = 0;
int CameraLoop(TreeNode* root)  //错误版本
{
    if (root == nullptr)
    {
        return -1;
    }
    int ret = 0;
    int left = CameraLoop(root->left);
    int right = CameraLoop(root->right);
    if (left == -1 && right == -1)
    {
        ret = 0;
    }
    else if ((left == -1 && right == 0) || (left == 0 && right == -1))
    {
        ++count;
        ret = 1;
    }
    else if ((left == 1 && right == -1) || (left == -1 && right == 1))
    {
        ret = 0;
    }
    else if ((left == 1 && right == 0) || (left == 0 && right == 1))
    {
        ++count;
        ret = 1;
    }
    else if (left == 1 && right == 1)
    {
        ret = 0;
    }
    else if (left == 0 && right == 0)
    {
        ++count;
        ret = 1;
    }
    return ret;
}

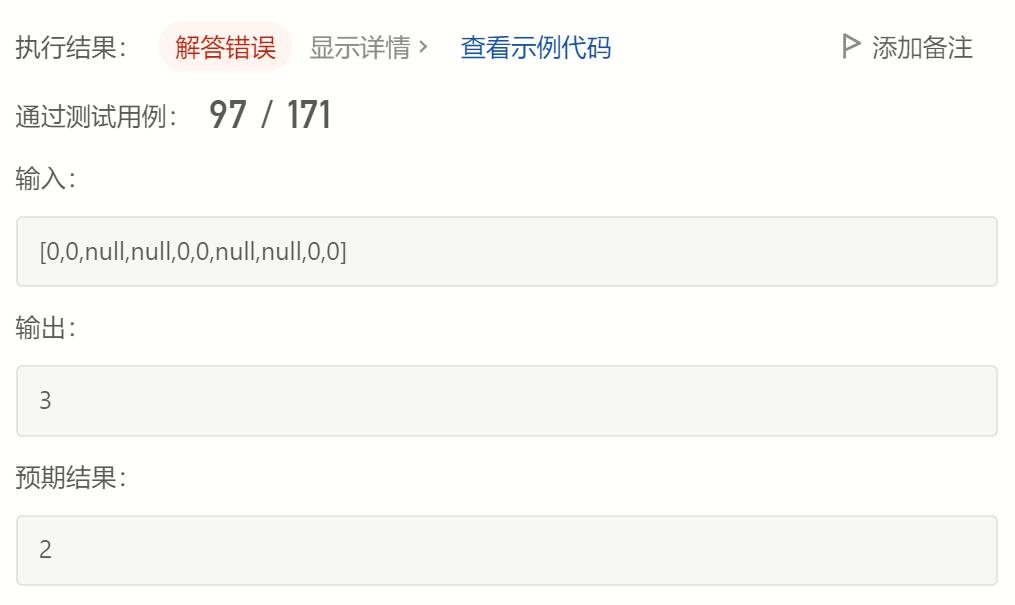
根据Carl哥的状态转移思路，写的一版

TreeNode* OriginRoot;
int CameraNum = 0;
int CameraLoop(TreeNode* root)
{
    if (root == nullptr)
    {
        return 2;
    }
    int left = CameraLoop(root->left);
    int right = CameraLoop(root->right);
    int ret = 0;
    ////若当前为整个树的根节点，且孩子中没有camera，要自己装一个
    if (root == OriginRoot && left != 1 && right != 1)
    {
        ++CameraNum;
    }
    else if (left == 2 && right == 2)  //叶子节点，无覆盖
    {
        ret = 0;
    }
    //if ((left == 0 && right == 2) || (left == 2 && right == 0))
    else if (left == 0 || right == 0)  //孩子中至少有一个没覆盖的，这里都要加camera
    {
        ++CameraNum;
        ret = 1;
    }
    else if (left == 1 || right == 1)  //孩子中至少有一个装了摄像头的，这里都无需再装
    {
        ret = 2;
    }
    return ret;
}