算法随想Day8【字符串】| LC28-实现 strStr() 、LC459-重复的子字符串

KMP算法

前缀是包含首字母，不包含尾字母的所有子串。

后缀是包含尾字母，不包含首字母的所有子串。

如有：

​ 文本串 aabaabaaf

​ 模式串 aabaaf

对模式串来说，其前后缀：

前缀有	后缀有
a	f
aa	af
aab	aaf
aaba	baaf
aabaa	abaaf

前缀表，通常被称为next数组

a	0
aa	1
aab	0
aaba	1
aabaa	2
aabaaf	0

这样就对模式串生成了一个序列：

a a b a a f

0 1 0 1 2 0

遇到第一个不匹配的字符时，如aabaaf匹配文本串，遇到第一个不匹配的为f字符，然后找f前面那个字符在序列中对应的数值（“2”），之后的匹配就不用从模式串的第一个a开始匹配了，可以从aabaa中的a开始，而b的索引下标刚好是最长相等前缀的长度 -- “2”。

next数组的实现

初始化：

• 前缀末尾：prefix_tail，同时也代表着suffix_tail，包括suffix_tail之前的子串的最长相等前后缀的长度

• 后缀末尾：suffix_tail，这里的后缀末尾指的是，如aabaa中的第三个"a"

需要比较前缀和后缀所对应的字符是否相等，因为后缀是不包含字符串的首字母的，所以suffix_tail应该初始化为1。

在建立next数组时，要考虑的情况有：

• 前后缀不相同的情况：不断地让prefix_tail往回退，直到重新与当前suffix匹配或回到字符串首字母
• 前后缀相同的情况：让prefix_tail向前走一步

void getNext(vector<int>& next, string s)
{
	int prefix_tail = 0;
    //vector<int> next(s.size(), 0)
    next[0] = 0;
	for (suffix_tail = 1; suffix_tail < s.size(); suffix_tail++)
    {
        while (prefix_tail > 0 && s[suffix_tail] != s[prefix_tail])
        {
            prefix_tail = next[prefix_tail - 1];
        }
        
        if (s[suffix_tail] == s[prefix_tail])
        {
            prefix_tail++;
        }
        next[suffix_tail] = prefix_tail;
    }
}

模拟运行过程时，从头遍历的是文本串，如若遇到某个模式串的字符与当前文本串指向字符不同的时候，让模式串的当前指针根据next表（ next[ptr_needle - 1] ）进行回退。

int strStr(string haystack, string needle)
{
    if (needle.size() == 0)  //和库函数strstr()保持一致
    {
        return 0;
    }
    int needle_size = needle.size();
    vector<int> next(needle_size, 0);
    getNext(next, needle);
    int ptr_needle = 0, ptr_haystack = 0;
    for (ptr_haystack = 0; ptr_haystack < haystack.size(); ptr_haystack++)
    {
        while (ptr_needle > 0 && needle[ptr_needle] != haystack[ptr_haystack])
        {
            ptr_needle = next[ptr_needle - 1];
        }
        if (needle[ptr_needle] == haystack[ptr_haystack])
        {
            ptr_needle++;
        }
        if (ptr_needle == needle_size)
        {
            return (ptr_haystack - needle_size + 1);
        }
    }
}

思考总结：

创建next数组和模拟运行，这两个过程的编码思想十分的相似，但又有些细节的不同。

• 创建next数组中，是在模式串中运用双指针，固定一个指针(suffix)用于遍历，而另一个prefix是根据suffix的行为而动态移动的。

• 模拟运行中，在文本串和模式串中各自应用一个指针，其中文本串的指针用于从头遍历，而模式串中的指针则根据前者的行为而动态移动。

LC459. 重复的子字符串

暴力解法

bool repeatedSubstringPattern(string s)
{
    int i, j;
    bool flag = true;
    int size = s.size();
    if (size < 2)
    {
        return false;
    }
    for (i = 1; i < (size >> 1); i++)  //这里要用<=，即对半分字符串的情况
    {
        if (size % i != 0)
        {
            continue;
        }
        flag = true;
        for (j = i; j < size; j++)
        {
            if (s[j] != s[j - i])
            {
                flag = false;
                break;
            }
        }
    }
    return flag;
}

移除匹配法：

bool repeatedSubstringPattern_erase(string s)
{
    string str = s + s;
    str.erase(str.begin());  //对新字符串进行掐头去尾
    str.erase(str.end() - 1);
    //新字符串中若能再出现s，说明满足题意
    if ((str.find(s)) == std::string::npos)
    {
        return false;
    }
    return true;
}

KMP妙解法：

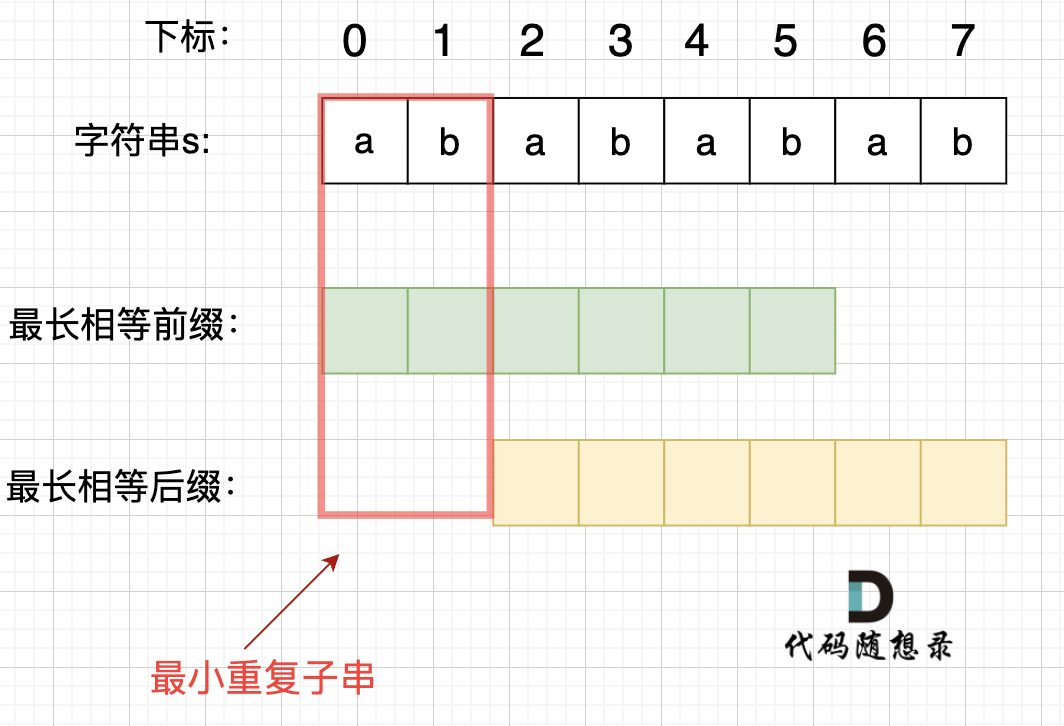
找到字符串的最长相等前后缀，如果该字符串是由重复的子字符串构成的，最长相等前缀和最长相等后缀是相同的，两者错开的长度，就是会重复的子字符串。

对abababab，next数组应该为00123456，通过数学公式，可推得：

next[len - 1] != 0 && len % (len - (next[len - 1] ) == 0

代码实现：

class Solution {
public:
    void getNext (int* next, const string& s){
        next[0] = 0;
        int j = 0;
        for(int i = 1;i < s.size(); i++){
            while(j > 0 && s[i] != s[j]) {
                j = next[j - 1];
            }
            if(s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }
    bool repeatedSubstringPattern (string s) {
        if (s.size() == 0) {
            return false;
        }
        int next[s.size()];
        getNext(next, s);
        int len = s.size();
        if (next[len - 1] != 0 && len % (len - (next[len - 1] )) == 0) {
            return true;
        }
        return false;
    }
};