算法随想Day6【哈希表】| LC454-四数之和Ⅱ、LC383-赎金信、LC15-三数之和、LC18-四数之和

LC454. 四数之和Ⅱ

先按O(n^2)将4组分成两组后，再按照两数之和的做法即可。其中umap中存储的value值是key出现的次数。

int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4)
{
    int i, j;
    int size = nums1.size();
    int temp = 0, count = 0;
    unordered_map<int, int> umap;
    ////分组(O(n^2))后再按照两数之和的做法
    for (i = 0; i < size; i++)
    {
        for (j = 0; j < size; j++)
        {
            temp = nums1[i] + nums2[j];
            umap[temp] = (umap.find(temp) != umap.end()) ? (umap[temp] + 1) : 1;
            //if (umap.find(temp) != umap.end())
        }
    }
    for (i = 0; i < size; i++)
    {
        for (j = 0; j < size; j++)
        {
            temp = nums3[i] + nums4[j];
            if (umap.find(0 - temp) != umap.end())
            {
                count += umap[0 - temp];
            }
        }
    }
    return count;
}

LC383. 赎金信

bool canConstruct(string ransomNote, string magazine)
{
    int i;
    int size = magazine.size();
    vector<int> vec_magaz(26, 0);
    if (ransomNote.size() > size)
    {
        return false;
    }
    for (i = 0; i < size; i++)
    {
        vec_magaz[magazine[i] - 97]++;
    }
    for (i = 0; i < ransomNote.size(); i++)
    {
        vec_magaz[ransomNote[i] - 97]--;
    }
    for (i = 0; i < 26; i++)
    {
        if (vec_magaz[i] < 0)
        {
            return false;
        }
    }
    return true;
}

LC15. 三数之和

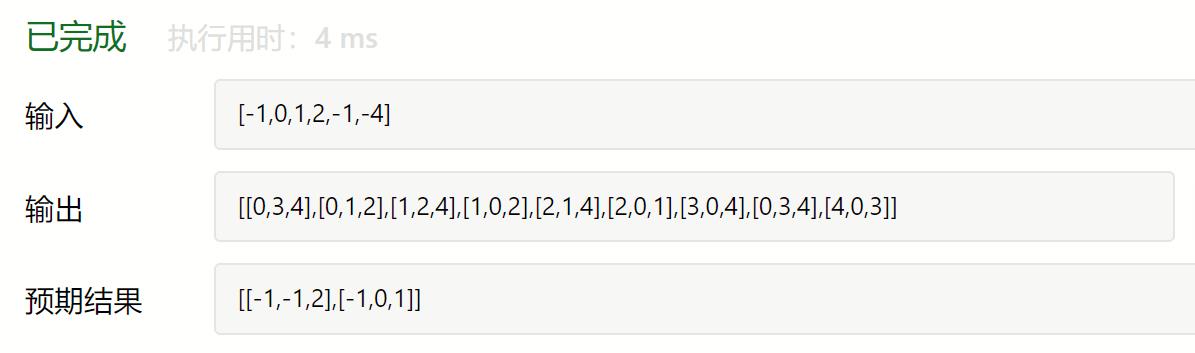
开始参照之前两数之和的思路，写了一个硬解的版本，但其实忽略的问题还是挺多的：

• 没审好题目，最好返回的是数值本身，而不是其对应的索引下标，所以可以先对整个向量进行排序的，因为即使被改变了下标，也不影响结果输出。

• 没考虑到结果需要的去重问题

vector<vector<int>> threeSum(vector<int>& nums)
{
    int i, j;
    int size = nums.size();
    vector<vector<int>> result;
    unordered_multimap<int, unordered_set<int>> umap;
    for (i = 0; i < size; i++)
    {
        for (j = i + 1; j < size; j++)
        {
            umap.insert(make_pair(nums[i] + nums[j], unordered_set<int>{i, j}));
        }
    }
    for (i = 0; i < size; i++)
    {
        //auto it = umap.begin();
        int a = 0 - nums[i];
        if (umap.find(0 - nums[i]) != umap.end())
        {
            for (auto it = umap.begin(); it != umap.end(); it++)
            {
                if (0 - nums[i] == it->first)
                {
                    it->second.insert(i);
                    if (3 == it->second.size())
                    {
                        result.push_back(vector<int>{it->second.begin(), it->second.end()});
                    }
                }
                
            }
        }
    }
    return result;
}

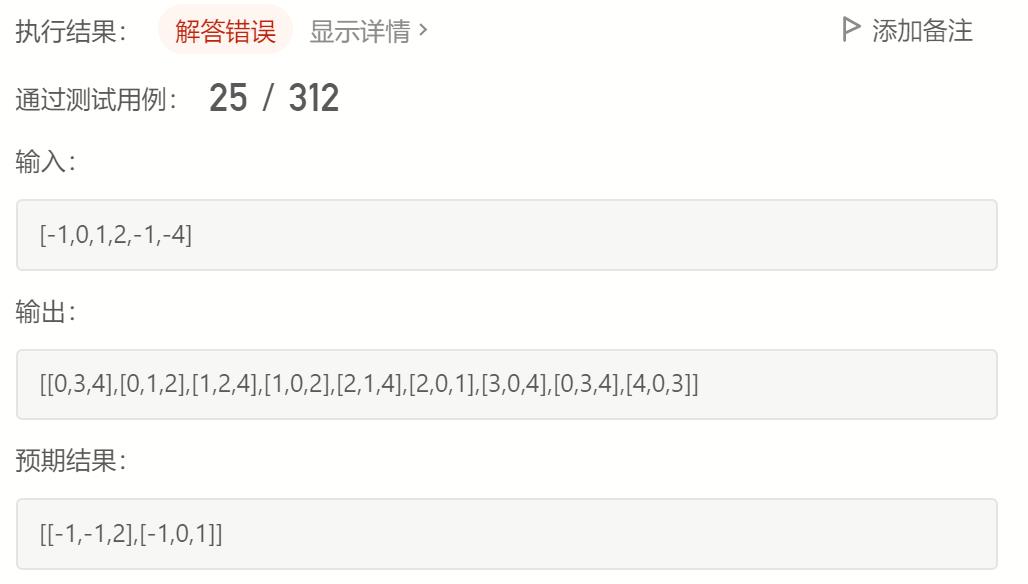
死缠烂打修改下，还是：

vector<vector<int>> threeSum(vector<int>& nums)
{
    int i, j;
    int size = nums.size();
    vector<vector<int>> result;
    unordered_multimap<int, vector<int>> umap;
    for (i = 0; i < size; i++)
    {
        for (j = i + 1; j < size; j++)
        {
            umap.insert(make_pair(nums[i] + nums[j], vector<int>{nums[i], nums[j]}));
            break;
        }
    }
    for (i = 0; i < size; i++)
    {
        //auto it = umap.begin();
        if (umap.find(0 - nums[i]) != umap.end())
        {
            for (auto it = umap.begin(); it != umap.end(); it++)
            {
                if (0 - nums[i] == it->first)
                {
                    it->second.push_back(nums[i]);
                    if (3 == it->second.size())
                    {
                        result.push_back(vector<int>{it->second.begin(), it->second.end()});
                    }
                }
                
            }
        }
    }
    return result;
}

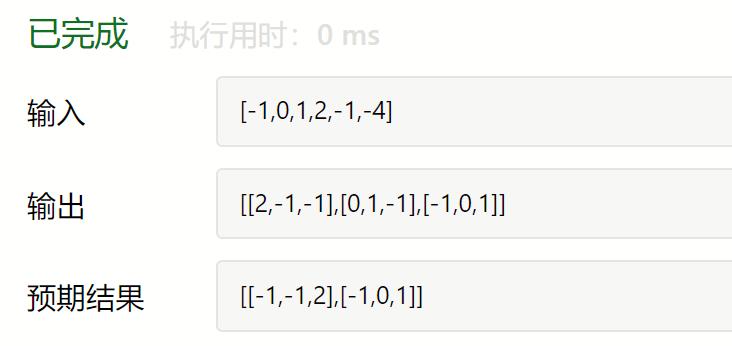
Carl讲解代码，思路：排序 + 双指针：

vector<vector<int>> threeSum(vector<int>& nums) {
    vector<vector<int>> result;
    sort(nums.begin(), nums.end());
    // 找出a + b + c = 0
    // a = nums[i], b = nums[left], c = nums[right]
    for (int i = 0; i < nums.size(); i++) {
        // 排序之后如果第一个元素已经大于零，那么无论如何组合都不可能凑成三元组，直接返回结果就可以了
        if (nums[i] > 0) {
            return result;
        }
        // 错误去重a方法，将会漏掉-1,-1,2 这种情况
        /*
        if (nums[i] == nums[i + 1]) {
            continue;
        }
        */
        // 正确去重a方法
        if (i > 0 && nums[i] == nums[i - 1]) {
            continue;
        }
        int left = i + 1;
        int right = nums.size() - 1;
        while (right > left) {
            // 去重复逻辑如果放在这里，0，0，0 的情况，可能直接导致 right<=left 了，从而漏掉了 0,0,0 这种三元组
            /*
            while (right > left && nums[right] == nums[right - 1]) right--;
            while (right > left && nums[left] == nums[left + 1]) left++;
            */
            if (nums[i] + nums[left] + nums[right] > 0) right--;
            else if (nums[i] + nums[left] + nums[right] < 0) left++;
            else {
                result.push_back(vector<int>{nums[i], nums[left], nums[right]});
                // 去重逻辑应该放在找到一个三元组之后，对b 和 c去重
                while (right > left && nums[right] == nums[right - 1]) right--;
                while (right > left && nums[left] == nums[left + 1]) left++;

                // 找到答案时，双指针同时收缩
                right--;
                left++;
            }
        }

    }
    return result;
}

LC18. 四数之和

四数之和，和三数之和是一个思路，都是使用双指针法, 基本解法就是在三数之和的基础上再套一层for循环。

对于三数之和，双指针法就是将原本暴力O(n^{3)的解法，降为O(n}2)的解法，四数之和的双指针解法就是将原本暴力O(n^{4)的解法，降为O(n}3)的解法。

双指针法将时间复杂度：O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级，题目如下：

• 27.移除元素
• 15.三数之和
• 18.四数之和

链表相关双指针题目：

• 206.反转链表
• 19.删除链表的倒数第N个节点
• 面试题 02.07. 链表相交
• 142题.环形链表II

vector<vector<int>> fourSum(vector<int>& nums, int target) {
    vector<vector<int>> result;
    sort(nums.begin(), nums.end());
    for (int k = 0; k < nums.size(); k++) {
        // 剪枝处理
        if (nums[k] > target && nums[k] >= 0) {
            break; // 这里使用break，统一通过最后的return返回
        }
        // 对nums[k]去重
        if (k > 0 && nums[k] == nums[k - 1]) {
            continue;
        }
        for (int i = k + 1; i < nums.size(); i++) {
            // 2级剪枝处理
            if (nums[k] + nums[i] > target && nums[k] + nums[i] >= 0) {
                break;
            }

            // 对nums[i]去重
            if (i > k + 1 && nums[i] == nums[i - 1]) {
                continue;
            }
            int left = i + 1;
            int right = nums.size() - 1;
            while (right > left) {
                // nums[k] + nums[i] + nums[left] + nums[right] > target 会溢出
                if ((long) nums[k] + nums[i] + nums[left] + nums[right] > target) {
                    right--;
                // nums[k] + nums[i] + nums[left] + nums[right] < target 会溢出
                } else if ((long) nums[k] + nums[i] + nums[left] + nums[right]  < target) {
                    left++;
                } else {
                    result.push_back(vector<int>{nums[k], nums[i], nums[left], nums[right]});
                    // 对nums[left]和nums[right]去重
                    while (right > left && nums[right] == nums[right - 1]) right--;
                    while (right > left && nums[left] == nums[left + 1]) left++;

                    // 找到答案时，双指针同时收缩
                    right--;
                    left++;
                }
            }

        }
    }
    return result;
}