[学习]leetCode Hot100刷题记录!

序言

由于最近发现自己在之前只注重于Java工程能力的提升,忽略了自己在算法和数据结构还有其他计算机基础能力上的提升,导致现在想投大厂发现自己的基础能力真的一坨,这样子对自己未来的发展肯定也不友好,所以打算在现在实习的间隙当中提升自己的基础能力,算法就从leetCodeHot100开始,有些算法现在还不会,所以我打算带着问题去学习.

2025/05/12 周一

1.两数之和

这道题的解法思路就是使用哈希表,哈希表的基础知识前面已经复习了解过了
使用一个HashMap记录已经遍历过的数据,key为数据,value为索引,如果当前的target减去当前遍历到的数字在map中有这个key,则直接返回value,也就是数组

private int[] solution(int[] nums, int target) {
        Map<Integer, Integer> data = new HashMap<>();
        data.put(nums[0], 0);
        for (int i = 1; i < nums.length; i++) {
            if (data.containsKey(target - nums[i])) {
                return new int[]{data.get(target - nums[i]), i};
            } else {
                data.put(nums[i], i);
            }
        }
        return null;
    }

这里如果不使用contains的话也可以直接get然后判断是否为空

49. 字母异位词分组

看到这道题的时候想到String可以转化成char数组,再由char数组进行排序后重组成String,如果字母相同就能得到相同的String.有思路之后就开始实现

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        List<List<String>> result = new ArrayList<>();
        if (strs == null || strs.length == 0) {
            return result;
        }
        Map<String, List<String>> map = new HashMap<>();
        for (String str : strs) {
            char[] charArray = str.toCharArray();
            Arrays.sort(charArray);
            String sorted = new String(charArray);
            if (!map.containsKey(sorted)) {
                map.put(sorted, new ArrayList<>());
            }
            map.get(sorted).add(str);
        }
        map.forEach((k, v) -> {
            result.add(v);
        });
        return result;
    }
}

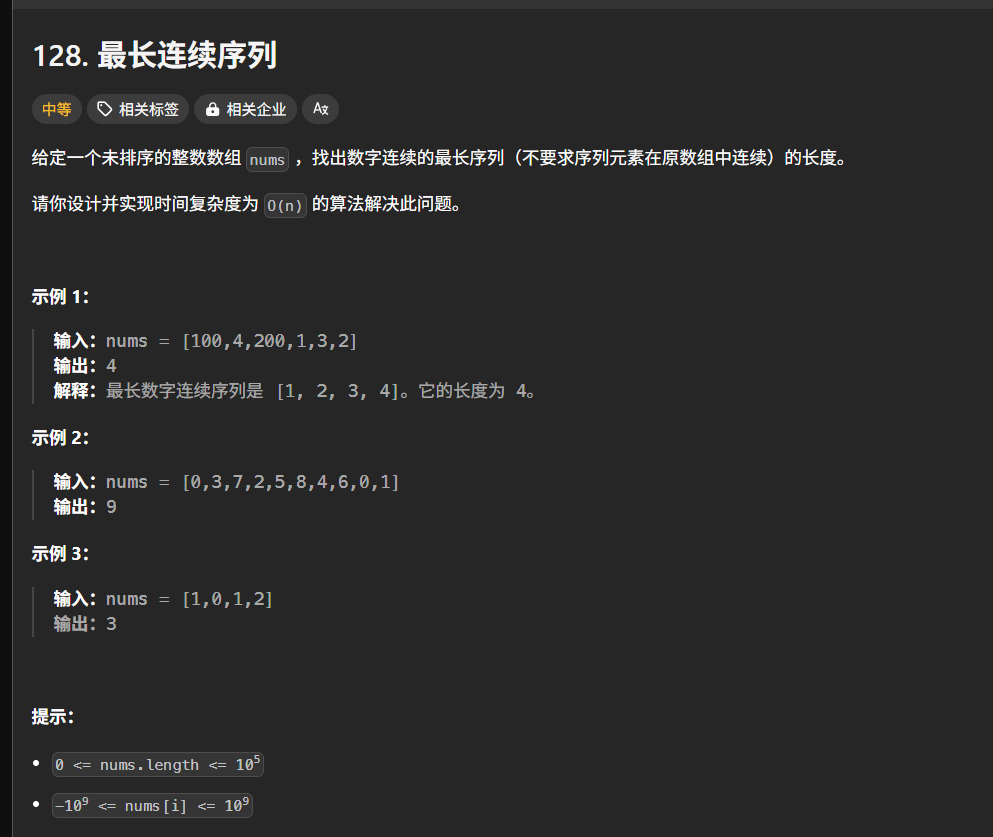
128. 最长连续序列-----(卡住)

说实话,看到这题我是一时间想不出什么思路的,后来去看了一下题解,一开始的思路就是想把无序的序列排序之后再使用HashMap进行去重,最后从第一位开始+1之后看下Map里面有没有这个key,但是这个有个问题,那就是Map是没有索引这种东西的,如果出现0,1,3,4,5,6,7,8这种序列就不好数了.所以这里想不出怎么办了~~(有想过HASHSET,但是用的不熟)~~
随后去看了一眼题解,题解的方式就是遍历HashSet当中的每一个key(hashSet就是用Hashmap原理去重,他的每一个Value都是Object,这里复习到了).

for (int integer : integers) {
		//查找当前的数是否为序列开始
            if (!integers.contains(integer - 1)) {
		//如果是序列开始的话那么将current序列开始的数字设置成当前遍历到的数字.
		//因为是取最长,所以这里使用currentResult记录当前序列的长度.
                int currentNum = integer;
                int currentResult = 1;
		//通过while遍历来确定序列长度,在这个循环结束之后比较currentResult和LongestResult谁更大
		//取最长
                while (integers.contains(currentNum + 1)) {
                    currentNum++;
                    currentResult++;
                }
                longestResult = Math.max(longestResult, currentResult);
            }
        }

完整代码:

class Solution {
    public int longestConsecutive(int[] nums) {
        Set<Integer> num_set = new HashSet<Integer>();
        for (int num : nums) {
            num_set.add(num);
        }

        int longestStreak = 0;

        for (int num : num_set) {
            if (!num_set.contains(num - 1)) {
                int currentNum = num;
                int currentStreak = 1;

                while (num_set.contains(currentNum + 1)) {
                    currentNum += 1;
                    currentStreak += 1;
                }

                longestStreak = Math.max(longestStreak, currentStreak);
            }
        }

        return longestStreak;
    }
}

复盘: 这道题在思考的时候要考虑去重和找到序列的开始,我一开始的HashMap的还是有缺陷.这个解决方案的思路钥匙就是查找当前数是否为序列开始,如果是则通过累加HashMapKey查找,此时的时间复杂度是O(1),每一次断序列都和前面的序列对比一下长度,取最长.

2025/05/13 周二

今天还是有点焦虑,就算开始学习稳步来了,一想到自己离自己喜欢的公司(哔哩哔哩,米哈游)还有这么远的距离,就想赶紧进步

283.移动零-----时隔一年又复习到双指针

为什么是时隔一年呢?因为上一次做算法还是刚刚正式系统的接触到计算机的时候,那时候就听说数据结构和算法很重要了,所以就开始看,但是因为基础薄弱所以就先搁置了.

这里使用到的是双指针这个概念,一个慢指针一个快指针.慢指针和快指针初始化在数组起始,快指针遍历数组,当遇到0的时候跳过,遇到非0的时候与慢指针交换数据,随后慢指针向前一位,具体实现如下:

private static void moveZeroes(int[] nums) {
        int slowPointer = 0;
        int fastPointer = 0;
        while (fastPointer < nums.length) {
            if (nums[fastPointer] != 0) {
                int temp = nums[slowPointer];
                nums[slowPointer] = nums[fastPointer];
                nums[fastPointer] = temp;
                slowPointer++;
            }
            fastPointer++;
        }
    }

这里我有个问题,也就是开头并不是0的时候,这样子不就发送快指针向前走,慢指针不动了吗?这里是我纯纯铸币了,当第一位也就是快慢指针在一起的时候,如果当前指针指向的data部位0,则双指针向前挪,慢指针只会停留在0上,而快指针不会停留在0上而是会继续向前走

11. 盛最多水的容器-----第一次接触到贪心算法

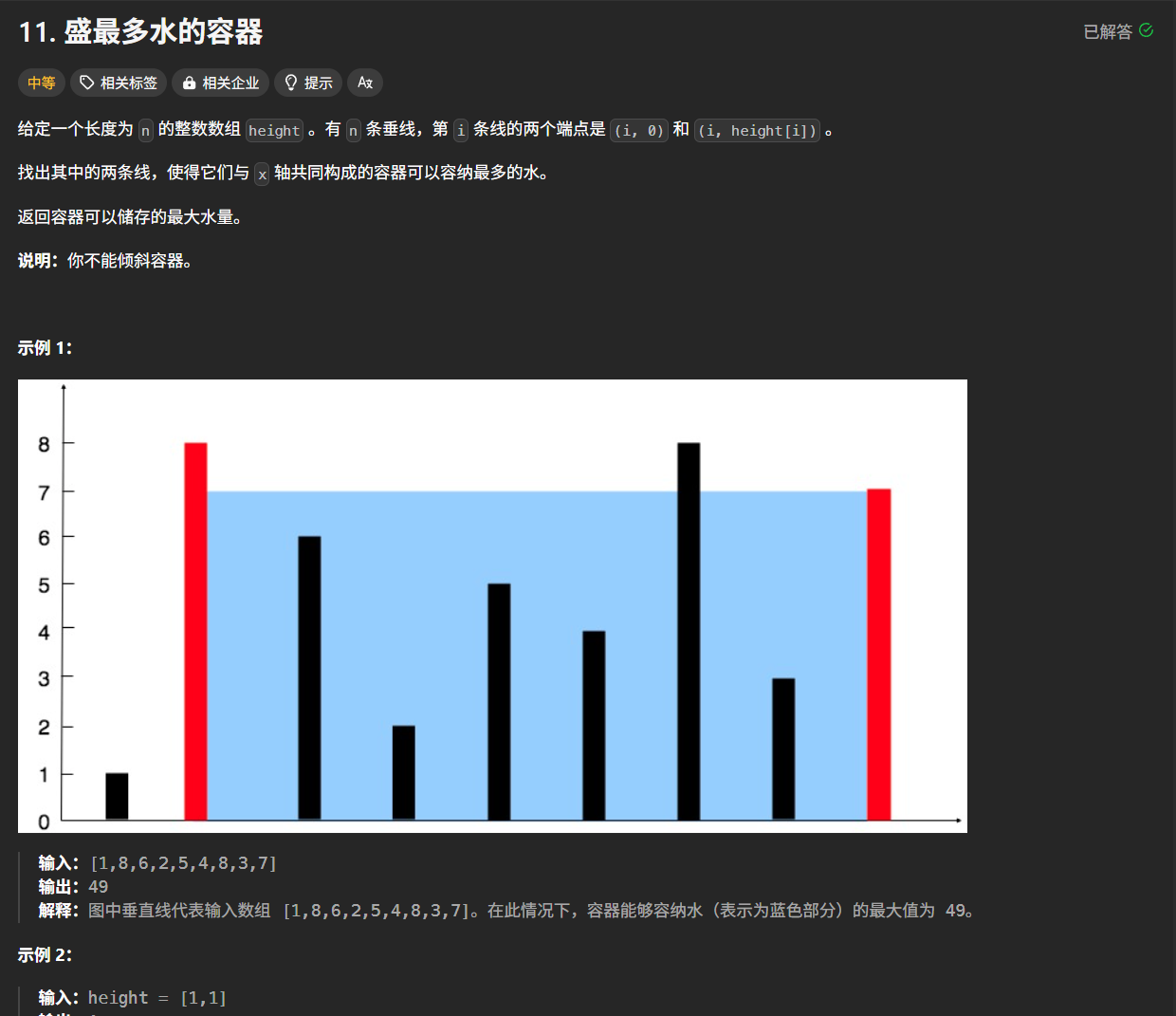
在第一次看到这道题目的时候,我愣住了,原因是我不知道怎么才算最大的,怎么找比较好.我一开始的思路就是使用双指针,但是双指针的实现思路就是一边不变,另一边持续向一边移动,每次移动的时候计算(最低顶点*路径)的面积,这样子左右都来一次,每次计算的时候都对比当前面前是否为最大面积,最后计算出最大面积.
这种思路在前面几个case的时候是没问题的,但是其中几个case是过不了,也就是说当前的这个算法存在着缺陷,然后我就去看了题解,当中用到了贪心算法,先来看代码吧

private static int maxArea(int[] height) {
        if (height.length < 2) {
            return 0;
        }
        int left = 0, right = height.length - 1;
        int max = 0;
        while (left < right) {
            max = Math.max(max, Math.min(height[left], height[right]) * (right - left));
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        return max;
    }

这里我们可以理出思路:
当节点少于2个的时候,不成立面积,直接返回0
初始化左右指针
当左边指针小于右边的的时候,循环计算面积
再令端点高度较低的一方向较高的一方移动,如果齐平则右边移动(这里参考贪心算法,是我不会的知识点,还要去学习)
当左右指针重合的时候,这时结束循环,返回循环中最大的面积.至此得到答案.
其实到这里我对这道题还是一知半解,为什么小的那边不能再作为容器的边界了?这里放个力扣官方解答的图作为参考,明天先着重学习一下贪心算法

2025/5/15 今天真的是上强度了

昨天回到家之后太累了,回来看了一下牛客,焦虑的不行没状态刷题

15.三数之和------双指针的运用

这道题说实话,我第一次看见真没什么思路,感觉算法题很有挫败感的一点也是这里,刚开始刷题没有经验,看到题目不知道用什么思路去解题
这里我们用到了双指针,先将这个数组进行排序,从小到大,这样子左边就一定是最小数,从左边开始遍历,左指针为i+1,右指针为nums.length-1,当i>0的时候,如果当前的数等于上一个数,例如 -1 -1 2,这里i=1的时候为-1,跟i-1 也是-1一样,就直接跳过这次循环,当left小于right的时候,就是经典的双指针开始互相前进,当i和左右指针相加大于0的时候,说明数字大了,要将大的指针往左移动,反之同理,在移动之后要检查一下移动后的指针指向跟上一个值是不是一样的,如果为0则为结果,加入list,再将指针移动一位.代码如下:

private static List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums);
        for (int i = 0; i < nums.length; i++) {
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            int left = i + 1, right = nums.length - 1;
            while (left < right) {
                if (nums[i]+nums[left]+nums[right]>0){
                    right--;

                }else if (nums[i]+nums[left]+nums[right]<0) {
                    left++;

                }else {
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    left++;
                    right--;
                    while (left < right && nums[left] == nums[left - 1]) {
                        left++;
                    }
                    while (left < right && nums[right] == nums[right + 1]) {
                        right--;
                    }
                }
            }
        }
        return result;
    }

42.接雨水-----这位更是重量级

今天看到这道题,感觉很像最大装水,最大装水的思想是贪婪思想和双指针,这道题适用双指针算法,不过主流的可能是前缀?还没彻底吃透,现在想知道以后如果遇到这种不会的算法题该怎么开始思考,这里先放个视频,过几天如果还知道怎么解的话或者理解透彻了就回来补上思路,因为现在写感觉有点像抄书
盛水最多的容器

2025/05/16 周五

今天没去公司,请假,思考自己的未来,非常内耗,找朋友出去喝了点聊了一下,发现很多时候不全是自己不够努力,而是整个就业环境就不是很好,没有好的学历所以基本没有机会去面试.

3. 无重复字符的最长子串------滑动窗口初见

第一次听到滑动窗口这个概念还是在学习TCP协议里面见到的,这里用到的滑动窗口可以学习一下这个思想.

2025/05/18 周日

56.合并区间

根据二维数组当中每个数组的第一个数进行排序,随后维护一个数组,判断第i个数组和当前list数组的最后一位关系

class Solution {
    public int[][] merge(int[][] intervals) {
        if (intervals.length == 0) {
            return new int[][]{};
        }
        List<int[]> res = new ArrayList<>();
        Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
        res.add(intervals[0]);
        for (int i = 1; i < intervals.length; i++) {
            if (res.getLast()[1] >= intervals[i][0]) {
                res.getLast()[1] = Math.max(res.getLast()[1], intervals[i][1]);
            } else {
                res.add(new int[]{intervals[i][0], intervals[i][1]});
            }
        }
        return res.toArray(new int[res.size()][]);
    }
}

2025/05/20------动态规划

最近在学习动态规划DP,看了代码随想录的教程,提供了一个很好的思路:动态规划五步法
1.确定dp数组及下标的含义
2.确定递推公式（状态转移方程）
3.初始化dp数组
4.确定遍历顺序
5.举例推导dp数组
这里我们先最简单的爬楼梯进行举例

这里我们先第一步,确认dp数组以及下标的含义,分析一下题目,这里的n台阶其实就是n-1阶和n-2阶方法的和,之后我们就开始第二部,确定推导公式,这里要注意一点dp[i]代表的是方法总和,而不是第几阶,
所有路径的最后一步只有两种可能：
从第3阶跨1阶到第4阶
这种路径的总数 = 爬到第3阶的方法数（dp[3]）
对应路径：1→2→3→4、1→3→4、2→3→4（共3种）
从第2阶跨2阶到第4阶
这种路径的总数 = 爬到第2阶的方法数（dp[2]）
对应路径：1→2→4、2→4（共2种）
我们能最先确定的两个下标就是0和1和2,这里的0定位成1(至于为什么去看代码随想录的动态规划视频),那么也就是dp[0]和dp[1]
之后再确定遍历顺序,这里根据题目是从前到后遍历

private static int climbStairs(int n) {
	//边界情况
        if (n <= 2) {
            return n;
        }
	//因为0台阶也算,所以这里n+1
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 2; i < dp.length; i++) {
            dp[i] = dp[i - 2] + dp[i - 1];
        }
        return dp[n];
    }

AC

总结:动态规划主要就是根据这五步法来解题.再多做点题灵活运用加深理解

2025/05/23------动态规划,数组

62.不同路径

跟我我们之前学习的动态规划五步法,这里我们先要确定dp数组的含义(这里题目题意就不多解释了),地图为一个二维数组,每一格为走到当前格子的路径数量,确定dp[i][j]为i,j时当前的路径数量;第二步就是确认推导公式了,这里我们可以看到机器人是从左上角下来的,也就是说其实往右下角走机器人只会从格子的左边和上边到达,所以这里dp[i][j] = dp[i][j-1]+dp[i-1][j];第三步就是初始化dp数组了,我们看到这里我们最上边和最左边都是一条直线,也就是说上面的每一个格子都是1(题目规定机器人只能走右边或下边,所以这里不存在从下面走上来);初始化完成之后我们就可以确定遍历顺序了,这是就是从左往右从前往后;最后打印数组;

private static int uniquePaths(int m, int n) {
//        确认dp含义
        int[][] dp = new int[m][n];
//        分析完推导公式 dp[i][j] = dp[i-1][j](上方)+dp[i][j-1](左方)
//        初始化边缘
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }

        return dp[m - 1][n - 1];
    }

63.不同路径II

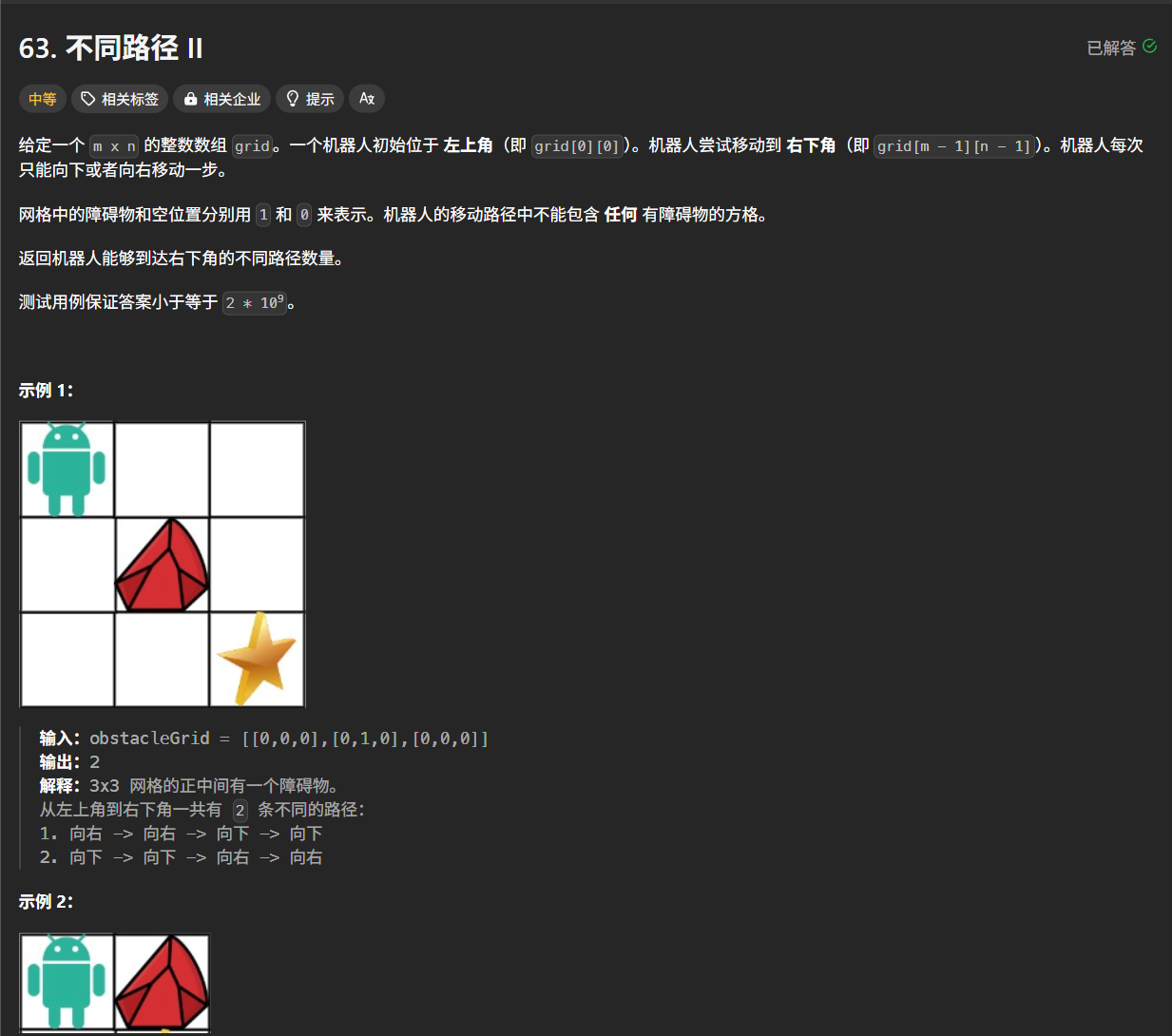
这题跟上一题的难度区别就是地图中间多了一个障碍.解题思路跟上一题相比,初始化的时候需要注意一下,当障碍物在最左边或者是最上边的时候,初始化过去时障碍物后面的都是0

private static int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];

        for (int i = 0; i < m; i++) {
            if (obstacleGrid[i][0] == 1) {
                break;
            }
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            if (obstacleGrid[0][i] == 1) {
                break;
            }
            dp[0][i] = 1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 0) {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
                System.out.print(dp[i][j]);
            }
            System.out.println();
        }
        return dp[m - 1][n - 1];
    }

因为有障碍的格子是1,所以0就是除了最左边和最上边之外没有走过的位置,所以只判断这些地方

343.整数拆分------有疑惑才会有进步

🔍 动态规划五步法分析

1. DP数组定义

dp[i]表示：

数字 i 拆分成至少两个数的和时，这些数的最大乘积。
- 比如 dp[4] = 4（因为 4 = 2 + 2，乘积 2×2=4 最大）。

2. 递推公式

目标：求dp[i]，我们要尝试所有可能的拆分方式：
- 把 i 拆成 j + (i-j)（j 从 1 到 i-1）。
- 对每种拆分方式，计算两种情况的乘积：
  1. 不继续拆分：直接乘 j × (i-j)（比如 5=2+3 → 2×3=6）。
  2. 继续拆分：j × dp[i-j]（比如 5=2+3，但 3 可以继续拆成 1+2 → 2×1×2=4）。
- 取这两种情况的最大值：max(j×(i-j), j×dp[i-j])。
- 最终 dp[i] 是所有 j 情况中的最大值。

3. DP数组初始化

dp[0] = 0, dp[1] = 0（因为不能拆分）。
dp[2] = 1（2=1+1，乘积是 1）。

4. 遍历顺序

从小到大计算：因为 dp[i] 依赖 dp[i-j]（比如算 dp[5] 需要 dp[4]、dp[3]）。

5. 举例验证

以 i=5 为例：

拆分方式	不继续拆分 (`j×(i-j)`)	继续拆分 (`j×dp[i-j]`)	最大值
`1 + 4`	`1×4 = 4`	`1×dp[4] = 1×4 = 4`	`4`
`2 + 3`	`2×3 = 6`	`2×dp[3] = 2×2 = 4`	`6`
`3 + 2`	`3×2 = 6`	`3×dp[2] = 3×1 = 3`	`6`
`4 + 1`	`4×1 = 4`	`4×dp[1] = 4×0 = 0`	`4`

最终 dp[5] = max(4, 6, 6, 4) = 6（最优拆法是 2+3 或 3+2）。

💡 关键问题：为什么要用 `dp[i-j]`？

你的例子：`i=5` 的拆法 `2 + 4`

你疑惑：“2×4=8 看起来很大，但 4 还能继续拆，会不会更大？”
实际上：
- 4 的最优拆法是 2+2=4（乘积 2×2=4）。
- 如果拆5=2+3：
  - 不继续拆：2×3=6。
  - 继续拆 3：3 的最优拆法是 1+2=3（乘积 1×2=2），所以 2×2=4。
  - 显然 6 > 4，所以直接 2×3=6 更好。

`dp[i-j]` 的作用

dp[i-j] 是 数字 i-j 的最优拆分乘积，它已经计算过所有可能的拆分方式！
它避免了重复计算：如果不用 dp[i-j]，你需要在每次拆 j + (i-j) 时重新计算 (i-j) 的拆分方式，效率极低。

dp[i]就是数字为i时能拆的最大乘积,这道题主要是加强了我对推导公式和动态规划的理解,动态规划的核心思想就是将每一步的最优解拆出来,一步步做到指定的值,所以要理解dp数组的含义,里面就是每一个步骤的最优解

posted @ 2025-05-12 22:19 MingHaiZ 阅读(188) 评论(0) 收藏举报

刷新页面返回顶部

MingHaiZ