【学习笔记】图论杂谈(二)
# 壹:【同余BFS】
- 同余最短路是处理线性组合表示数或最小代价满足同余条件问题的利器。
- 核心思想:用最短路算法维护不同同余类的最小代价,将数论问题转化为图上最短路问题。
【Problem】
# 贰:【差分约束】
不做详细探究
最短路跑的是 \(<=0\) 的最大值,最长路跑的是 \(>=0\) 的最小值
负环无解原因:至少有一组不等式永远无法被满足
【Problem】
# 参:【2-SAT】
一:【问题描述】
有 \(n\) 个变量, \(m\) 个限制, \(n\) 个变量取值为 \({0,1}\) ,求是否存在解,使得满足 \(m\) 个限制
\(m\) 个限制都可以转化为以下形式:若 \(A\) 取 \(a\) ,则 \(B\) 取 \(b\)
二:【解法】
对于以上问题,有一个求解的套路
对于一个变量 \(A\) 建两个点 \((A,A')\) ,分别表取 \((1,0)\)
对于一个限制 \(W\) 转化成若干条有向边 \(u->v\) ,表 \(u\) 成立则 \(v\) 成立
如果存在 \(A\) 和 \(A'\) 在同一个 \(SCC\) 中,则无解
若有解,对于每个二元组 \((A,A')\) 取其中拓扑序较大的点(即 \(SCC\) 编号较小的点)
三:【证明】
1.【如果存在 \(A\) 和 \(A'\) 在同一个 \(SCC\) 中,则无解】
如果 \(A\) 和 \(A'\) 在同一个 \(SCC\) 中,则两个都需要成立
然而 \(A\) 和 \(A'\) 本身是互斥关系(仅有一个成立),逻辑矛盾,所以无解
2.【如果不存在 \(A\) 和 \(A'\) 在同一个 \(SCC\) 中,则一定有解】
如果 \(A\) 和 \(A'\) 弱联通,钦定 \(A\) 的拓扑序小于 \(A'\) 的拓扑序
则有 \(A\) 成立则 \(A'\) 成立, \(A'\) 成立不一定 \(A\) 成立,所以可以取 \(A'\)
如果 \(A\) 和 \(A'\) 不连通,则 \(A\) 和 \(A'\) 任取其一
综上所述,对于每个变量 \(A\) 都可以取拓扑序较大的点 \(A'\)
所以有解
【Problem】
# 肆:【欧拉回路】
一:【定义】
- 【欧拉路径】:不重不漏经过每条边的路径
- 【欧拉回路】:起点终点相同的欧拉路径
- 【半欧拉图】:只存在欧拉路径的图
- 【欧拉图】:存在欧拉回路的图
这里定义
- 有向图中 \(otd\) 为出度, \(ind\) 为入度
- 无向图中 \(ind\) 为度数
二:【判定】
以下边都需要联通
1.【半欧拉图】
【有向图】
- 有两个点,一个点 \(S\) 满足 \(otd==ind+1\) ,一个点 \(T\) 满足 \(ind==otd+1\)
- 其他点满足 \(ind==otd\)
【无向图】
- 有两个点,满足 \(ind\) 为奇数,任意钦定 \(S,T\)
- 其他点满足 \(ind\) 为偶数
2.【欧拉图】
【有向图】
- 所有点满足 \(ind==otd\) ,任意钦定 \(S=T\)
【无向图】
- 所有点满足 \(ind\) 为偶数,任意钦定 \(S=T\)
三:【求解】
有向图欧拉路径,无向图欧拉路径,有向图欧拉回路,无向图欧拉回路,求解方法相同,故不分类讨论
从 \(S\) 处 \(DFS\) ,遇到 \(T\) 回溯,回溯时把点加入序列
需要加当前弧优化,否则复杂度错误
四:【证明】
1.【四个判定】
- 可以用环分解证明
很显然,感觉没用,懒得学
2.【回溯时加入序列】
画个图感性理解
【Problem】
# 伍:【三四元环计数】
三四元环都是对于无向图而言的,它们的定义看名字就好了
这里先讨论三四元环求解的共同步骤,再分开讨论
这里定义无向图度数为 \(deg\) ,有向图出度为 \(otd\) ,入度 \(ind\)
一:【共同步骤】
将边定向, \(deg\) 小的指向 \(deg\) 大的,如果相同,编号小的指向编号大的
新建图为 \(DAG\) ,且每个点的 \(otd<=\sqrt{m}\)
1.【 \(DAG\) 证明】
\(deg\) 和编号的大小比对满足传递性,所以新建图为 \(DAG\)
2.【 \(otd\) 限制】
这里采取反证
如果存在一个点 \(otd>=\sqrt{m}+1\) ,则有至少\(\sqrt{m}+1\)个点的\(otd>=\sqrt{m}+1\)
度数之和至少为 \({(\sqrt{m}+1)}^2=m+1+\sqrt{m}>m\),不存在
所以 \(otd<=\sqrt{m}\)
二:【三元环】
无向图的三元环 \((u,v,w)\) ,转为有向图后,有且仅有以下一种形式
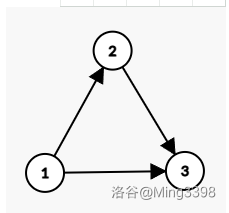
我们在 \(u\) 处统计答案
即枚举 \(u\) ,对 \(u\) 的所有出点打上标记
枚举 \(u\) 的出点 \(v\) ,枚举 \(v\) 的出点 \(w\)
如果 \(w\) 被打上了标记, \(ans++\)
复杂度 \(O(m\sqrt{m})\)
int ans = 0;
for(int i = 1; i <= n; ++i) {
for(int v : out[i]) vis[v] = 1;
for(int v : out[i]) for(int w : out[v]) if(vis[w]) ++ans;
for(int v : out[i]) vis[v] = 0;
}
三:【四元环】
无向图的四元环 \((u,v,w,x)\) ,转为有向图后,有多种形式,可以用一张图简单表示
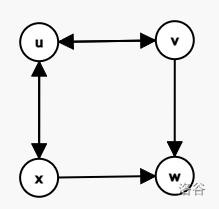
感性理解这张图:三元环 \((v,w,x)\) 的 \((v,x)\) 边上多了 \(u\) ,反向思考,对于一个点 \(u\) ,枚举其邻点 \(v\) ,对 \(v\) 做三元环计数(其中一条边靠 \(x\) 枚举,一条边自己枚举)
我们枚举 \(u\),再用原图边枚举 \(v\) ,再枚举 \(v\) 的出点 \(w\) ,把贡献记在 \(w\) 上,暴力统计答案(这里要求 \(deg_u<deg_w\) ,保证不会被重复统计)
复杂度 $O(m\sqrt{m}) $
int ans = 0;
for(int i = 1; i <= n; ++i) {
static int f[maxn];
for(int v : to[i]) for(int w : out[v]) if(cmp(i, w)) ans += f[w]++;
for(int v : to[i]) for(int w : out[v]) f[w] = 0;
}
【Problem】
# 陆:【最小树形图】
十级考纲懒得学



 浙公网安备 33010602011771号
浙公网安备 33010602011771号