算法系列之复杂度
认识复杂度
评估算法优劣的核心指标是什么?
- 时间复杂度(流程决定)
- 额外空间复杂度(流程决定)
- 常数项时间(实现细节决定)
时间复杂度
何为常数时间的操作?
如果一个操作的执行时间不以具体样本量为转移,每次执行时间都是固定时间。称这样的操作为常数时间操作。
常见的常数时间的操作
- 常见的算术运算(+、-、*、/、%等)
- 常见的位运算(>>、>>>、<<、|、&、^等)
- 赋值、比较、自增、自减操作等
- 数组寻址操作
总之,执行时间固定的操作,都是常数时间的操作。
反之,执行事件不固定的操作,都不是常数时间的操作。
如何确定算法流程的总操作数量与样本数量之间的表达式关系?
- 想象该算法流程所处理的数据状况,要按照最差情况来。
- 把整个流程彻底拆分为一个个基本动作,保证每个动作都是常数时间的操作。
- 如果数据量为N,看看基本动作的数量和N是什么关系。
如何确定算法流程的时间复杂度?
当完成了表达式的建立,只要把最高阶项留下即可。低阶项都去掉,高阶项的系数也去掉。即为
时间复杂度的意义:衡量算法流程的复杂程度的一种指标,该指标只与数据量有关,与过程之外的优化无关。
时间复杂度的估算
- 选择排序
- 冒泡排序
- 插入排序
选择排序
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
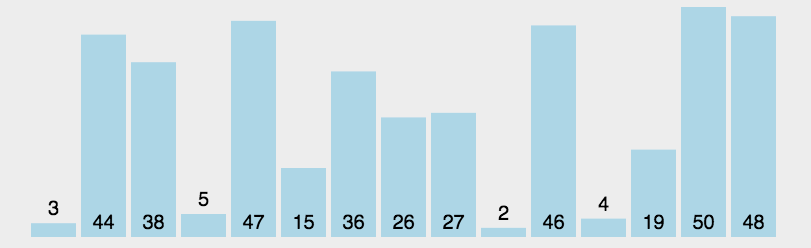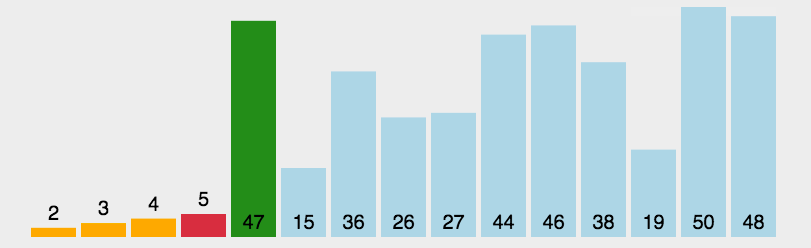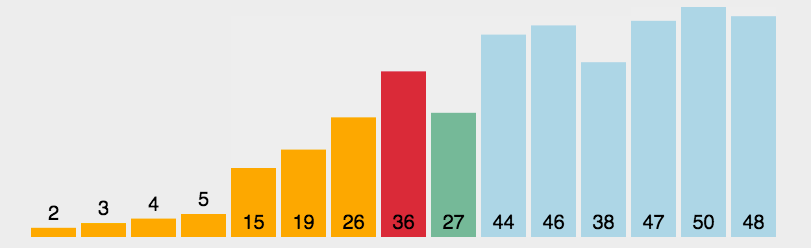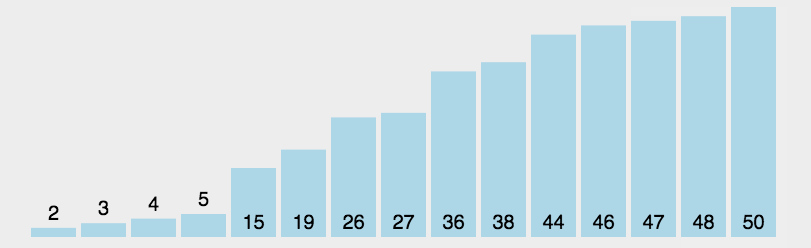
实现
public class SelectionSort {
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
// 0 ~ N-1
// 1 ~ N-1
// ...
for (int i = 0; i < arr.length; i++) {
// 最小值在哪个位置上 i ~ N-1
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) { // i ~ N-1 上找最小值的下标
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, minIndex, i);
}
}
private static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
分析过程:
- 在
arr[0, n-1]中,找到最小值所在的位置,然后把最小值交换到0位置。 - 在
arr[1, n-1]中,找到最小值所在的位置,然后把最小值交换到1位置。 - 在
arr[2, n-1]中,找到最小值所在的位置,然后把最小值交换到2位置。 - …
- 在
arr[n-1, n-1]中,找到最小值所在的位置,然后把最小值交换到N-1位置。
由上述过程可知,当arr数组的长度为n时,第一步常数操作的数量为N,第二步常数操作的数量为N-1,第三步常数操作的数量为N-2,以此类推,直到常数操作的数量为1。
很容易看出,此流程的常数操作的数量为一个等差数列。
如果一个等差数列的首项记作 a,公差记作 d,那么该等差数列第 n 项 an 的一般项为:
而一个等差数列的和,等于其首项与末项的和,乘以项数除以2。
公式证明如下:
将等差数列和写作以下两种形式:
将两公式相加来消掉公差 d,可得
带入(2)式,可得第二种及第三种形式。
从上面的第三种形式展开可见,任意一个可以写成
形成的数列和,其原来数列都是一个等差数列,其中公差 d = 2q,首项 a = p + q。
时间复杂度,该指标只与数据量有关,与过程之外的优化无关。因此总的常数操作数量为:
其中a,b,c为常数,根据(1)式可得:选择排序的时间复杂度为
冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
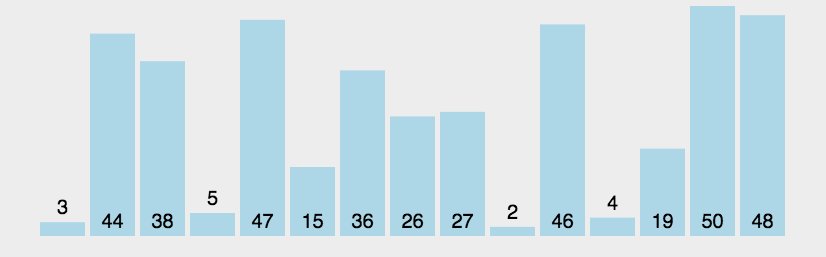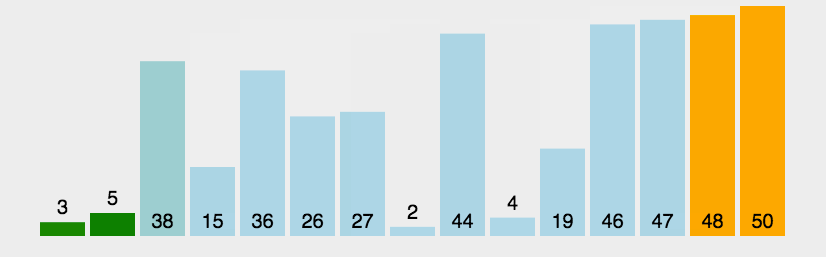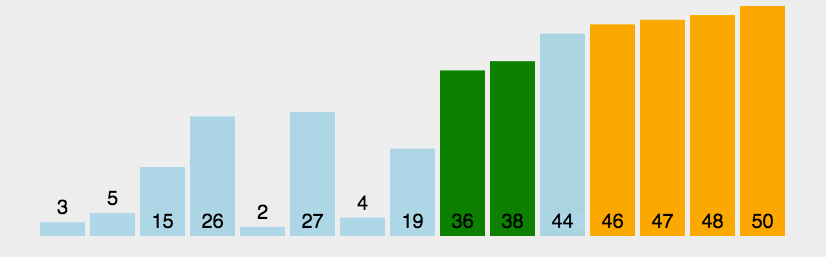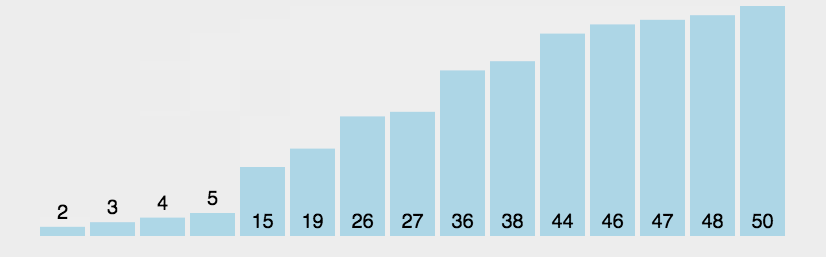
实现
public class BubbleSort {
public static void bubbleSort(int[] arr) {
if (arr == null | arr.length < 2) {
return;
}
for (int e = arr.length - 1; e > 0; e--) {
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}
private static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
分析过程:
- 在
arr[0, n-1]中,i的取值范围为[0, e),而e的取值范围为(0, arr.length-1],arr[i]和arr[i+1]比较,较大的值向后移 - 在
arr[0, n-2]中,i的取值范围为[0, e),而e的取值范围为(0, arr.length-2],arr[i]和arr[i+1]比较,较大的值向后移 - 在
arr[0, n-3]中,i的取值范围为[0, e),而e的取值范围为(0, arr.length-3],arr[i]和arr[i+1]比较,较大的值向后移 - …
- 在
arr[0, 1]中,重复上述过程,执行完毕。
由上述过程可知,当arr数组的长度为n时,第一步常数操作的数量为n-1,第二步常数操作的数量为N-2,第三步常数操作的数量为N-3,以此类推,直到常数操作的数量为1。
很容易看出,此流程的常数操作的数量为一个等差数列。
证明详见(2)~(8),所以,冒泡排序的时间复杂度为:
插入排序
插入排序(Insertion sort)是一种简单直观且稳定的排序算法。如果有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,但要求插入后此数据序列仍然有序,这个时候就要用到一种新的排序方法——插入排序法,插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序,
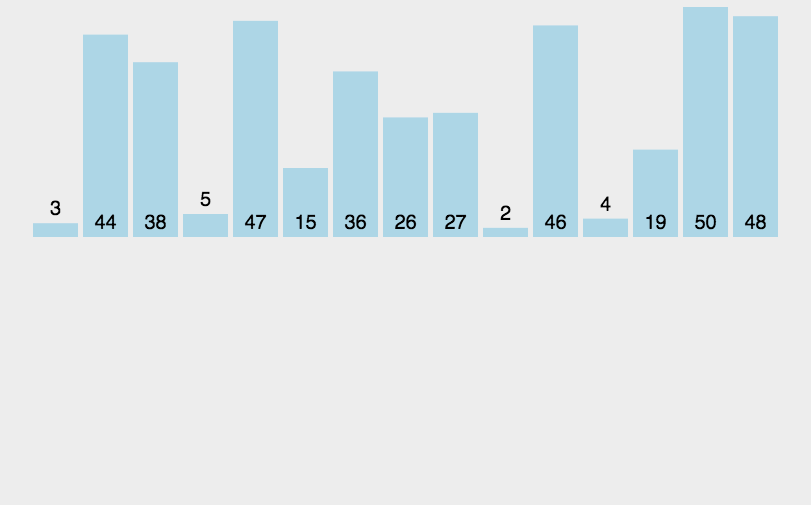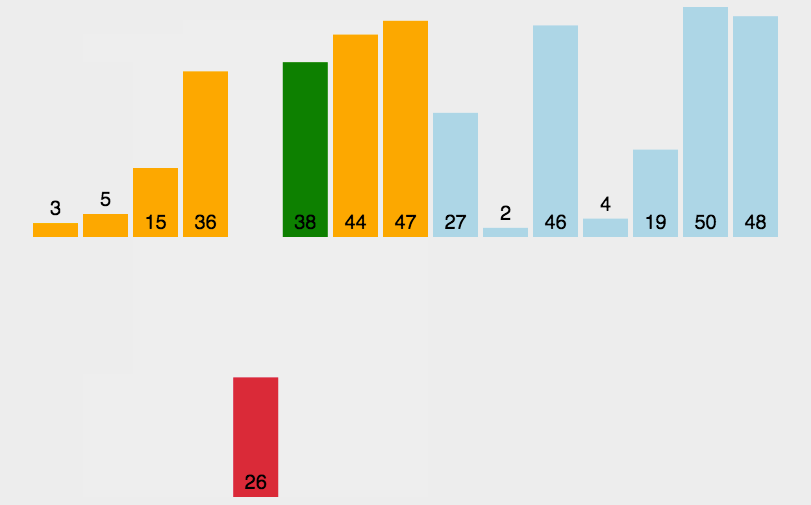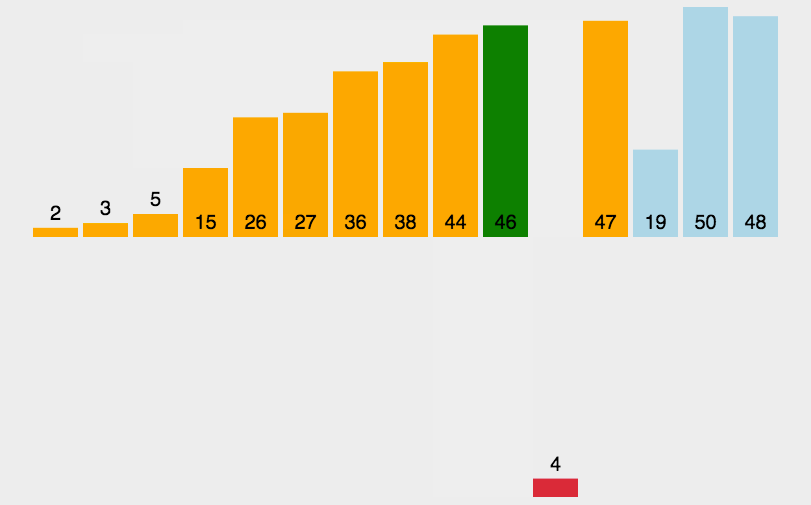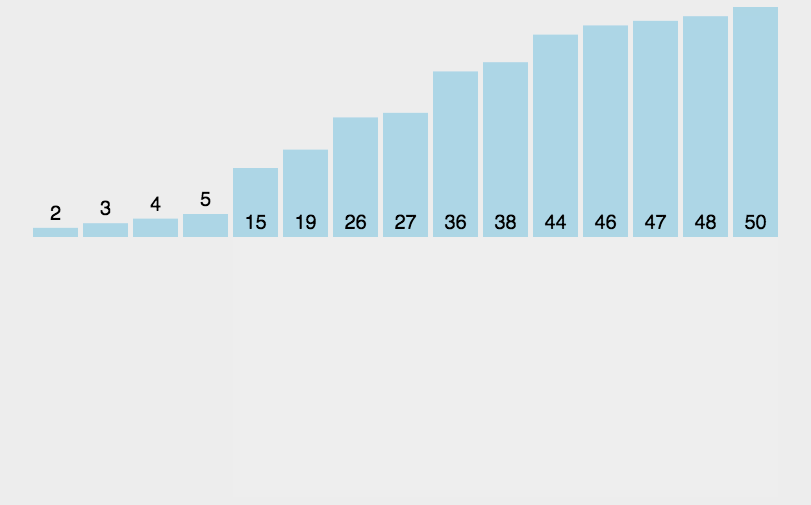
实现
public class InsertionSort {
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 1; i < arr.length; i++) {
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
private static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
分析过程:
- 令
arr[0, 0]上有序,这个范围内只有一个数,默认有序。 - 令
arr[0, 1]上有序,从arr[1]与之前的元素对比,如果arr[1]<arr[0],交换,否则不交换。 - …
- 令
arr[0, i]上有序,从arr[i]与之前的元素对比,如果arr[i]<arr[j](j的取值范围为[0, i-1]),交换,否则不交换,继续进行对比。 - 最后,想让
arr[1, n-1]上有序,arr[n-1]不停向左移动,直到数组左边的元素比arr[n-1]小时,停止移动。
实际估算时,这个算法流程的复杂程度,会因数据的排列状况不同而不同。按处理流程复杂度的原则来看,此时,按照最坏情况处理:
即数组为降序排列,而插入排序将数组改为升序。
由上述流程可得,,当arr数组的长度为n时,第一步常数操作的数量为1,第二步常数操作的数量为2,第三步常数操作的数量为3,以此类推,直到常数操作的数量为n-1。
很容易看出,此流程的常数操作的数量为一个等差数列。
证明详见(2)~(8),所以,冒泡排序的时间复杂度为:
注意
- 算法的过程,和具体的语言无关。
- 若要分析一个算法流程的时间复杂度,那么需要对该流程非常熟悉
- 一定要确保在拆分算法流程时,拆分出来的所有行为都是常数时间的操作。
常见的时间复杂度
效率从快到慢:
- O(1)
- O(logN)
- O(N)
- O(N*logN)
- O(N^2) O(N^3) … O(N^K)
- O(2^N) O(3^N) … O(K^N)
- O(N!)
额外空间复杂度
在算法流程中,需要开辟一些空间来支持算法流程。如果所需的空间是必要的、与现实目标有关的,则不算额外空间,即:
作为输入参数的空间,不算额外空间。
作为输出结果的空间,也不算额外空间。
除此之外,流程中如果还需要开辟空间才能使流程继续下去,那么,这部分空间就是额外空间。
如果流程中只需要开辟有限几个变量,额外空间复杂度为O(1)。
常数项时间
在处理时间复杂度时,通常将常数项时间忽略,因为,当n趋于无穷大时,常数项对一个算法的影响忽略不计。
但是,当两个算法对其时间复杂度相比较时,两个算法高阶项相同,例如:同为O(N)。那么此时,就需要对比常数项时间。
而常数项时间的对比,需要有深厚的功底,掌握流程中的每个细节,有一个简单的办法是,直接测试(控制变量),让后计算时间。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号