跟着迪哥学Python数据分析和机器学习(三）

数据分析与预处理

查看样本数据是否均衡

 

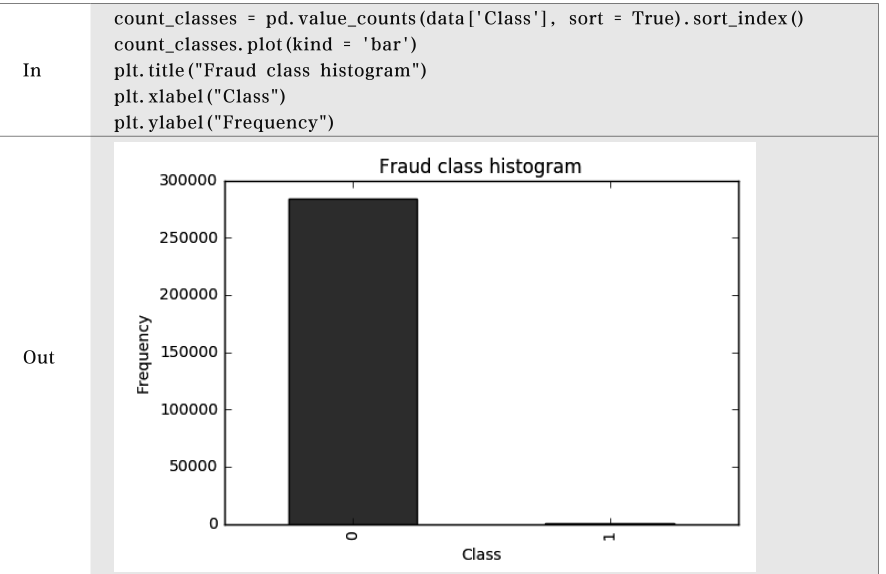
 样本不均衡解决方案

（1）下采样

　　让正常样本和异常样本数据一样少。

　　缺点：原始数据很丰富，下采样过后，只利用了其中一小部分。

（2）过采样

　　让异常样本和正常样本一样多。

　　缺点：异常数据是造出来的。

特征标准化

数据特征决定结果的上限，而模型的调优只决定如何接近这个上限

 　　特征标准化就是希望数据经过处理后得到的每一个特征的数值都在较小范围内浮动，公式如下：

$Z=\frac{X-X_{mean} }{std(X)} $

其中$Z$为标准化后的数据

$X$为原始数据

$X_{mean}$为原始数据的均值

$std(X)$为原始数据的标准差

过程分解：

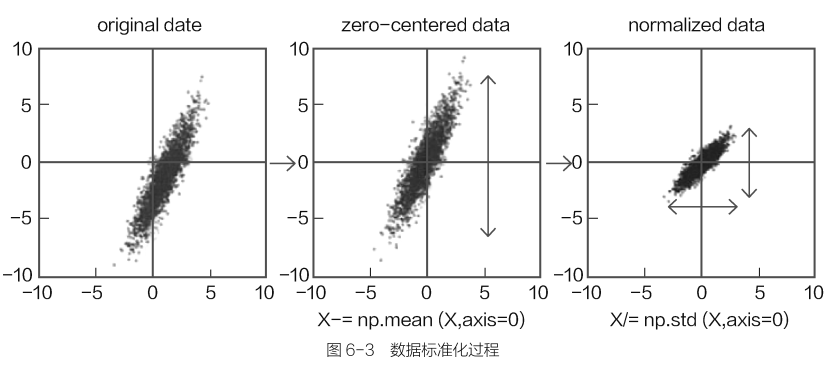
　　①将数据的各个维度减去其各自的均值，这样数据就以原点为中心对称。其中数值浮动较大的数据，其标准差也必然更大；数值浮动较小的数据，其标准差也会比较小。

　　②再将结果除以各自的标准差，就相当于当大的数据压缩到较小的空间中，让小的数据能够伸张一些。

数据标准化过程

 

 

 　　sklearn工具包核心三大板块：Classification、Regression、Clustering，以及数据降维（Dimensionality reduction）、模型选择（Model selection）、数据预处理（Preprocessing）

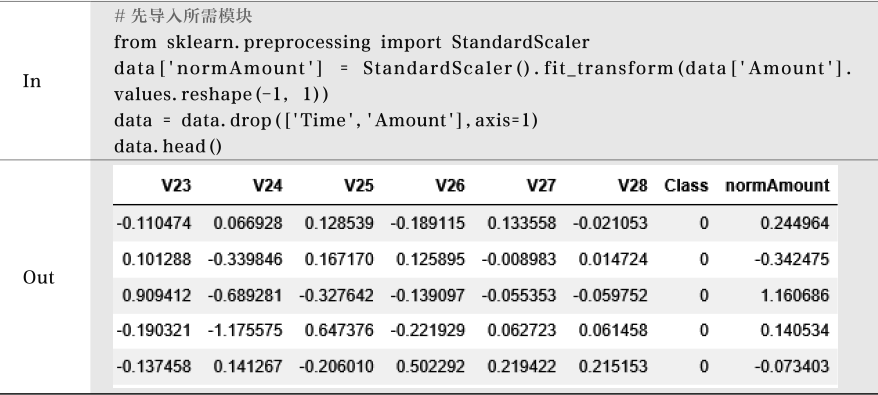
　　使用sklearn工具包来完成特征标准化操作

 

 下采样方案

　　对正常样本进行采样，得到与异常样本一样多的个数即可。

　　交叉验证：把训练集切分成多份，例如分成10份。在验证某一次结果时，需要把整个过程分成10步，第一步用前9份当做训练集，最后一份当做验证集，得到一个结果。以此类推，每次都依次用另外一份当做验证集，其他部分当做训练集。这样经过10步之后，就得到10个结果，每个结果分别对应其中每一小份，组合在一起恰好包含原始训练集中所有数据，再对最终得到的10个结果进行平均，就得到最终模型评估的结果。

 

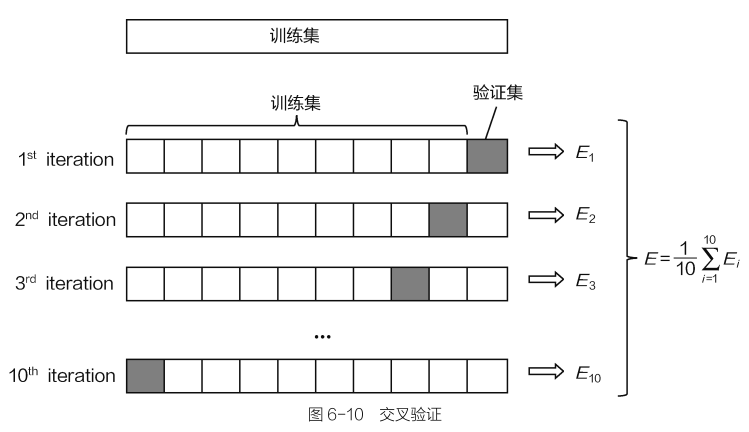
模型评估方法

　　准确率：准确率=符合条件的测定值个数/总测定值个数*100%=分类器正确分类的样本数与总样本数之比。

　　召回率（recall）：观察给定目标，针对这个目标统计你取得了多大成绩，而不是针对整体而言。

TP、TN、FP、FN：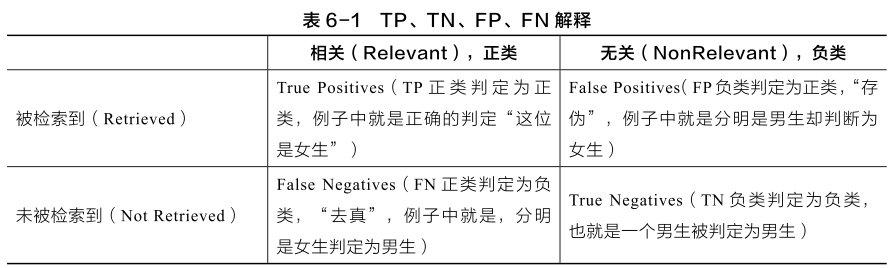

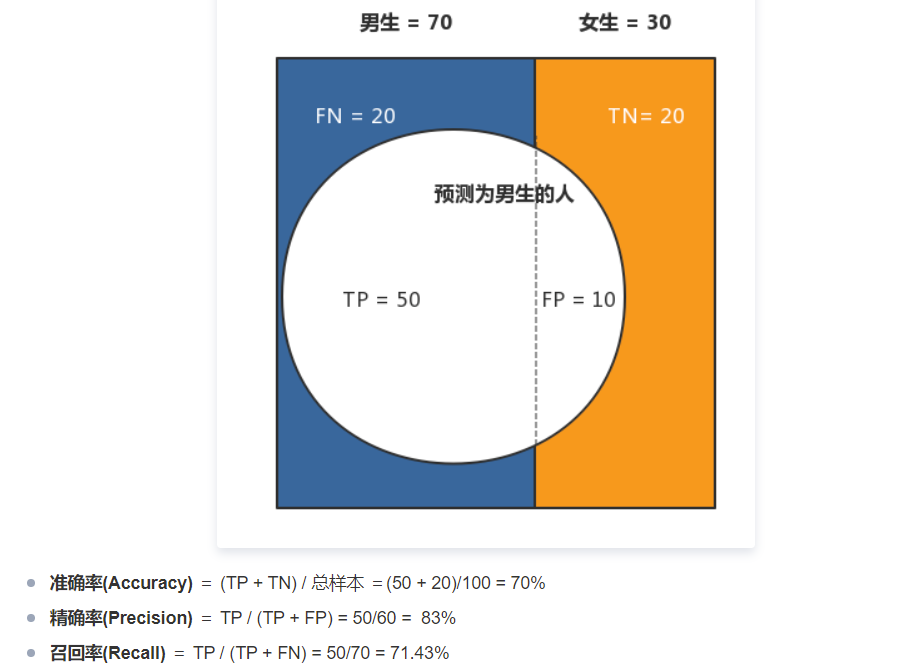
• 准确率（Accuracy）:表示在分类问题中，做对的占总体的百分比。

　　          $Accuracy=\frac{TP+TN}{TP+TN+FP+FN} $

• 召回率（Recall）：表示在正例中有多少能预测到，覆盖面的大小

　　　　   $Recall=\frac{TP}{TP+FN} $

• 精确度（Precision）:表示被分为正例中实际为正例的比例

　　　　   $P=\frac{TP}{TP+FP} $

正则化惩罚

 

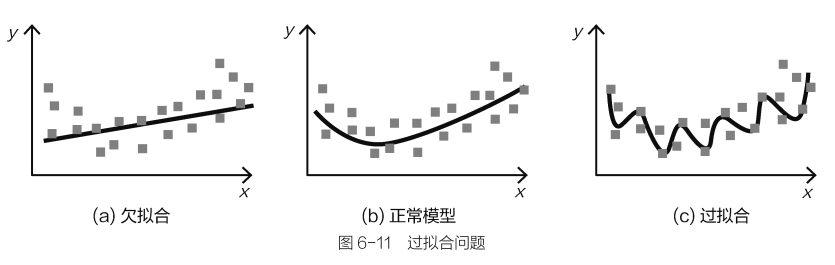
　　在机器学习中，通常都是先用简单的模型进行尝试，如果达不到要求，再做复杂一点的，而不是先用最复杂的模型来做。

　　过拟合：训练集效果越来越好，但是测试集效果反而越来越差。

　　对于统一算法，模型的复杂成都由其中要求解的参数（例如梯度下降中优化的参数）来控制。正则化惩罚就是为解决过拟合准备的，即惩罚数值较大的权重参数，让它们对结果的影响小一点。

　　惩罚项：用于惩罚那些模型参数，惩罚项会与目标函数组合在一起，让模型在迭代过程中就开始重视这个问题，而不是见面完成后再来调整。

　　常见有L1和L2正则化惩罚项：

　　　　L1正则化：$J=J_{0} +\alpha \sum_{w}^{} |w|$

　　　　　　此种方式下，$\theta _{1} :[1,0,0,0],\theta _{2} :[0.25,0.25,0.25,0.25]$结果仍然相同。

　　　　L2正则化：$J=J_{0} +\alpha \sum_{w}^{}w^{2} $

　　　　　　惩罚力度更大，对权重参数求平方和，目的就是让大的更大，相对惩罚更多。$\theta _{1} $的惩罚为1，$\theta _{2} $的惩罚只有0.25，表明$\theta _{1} $带来的损失更大，在模型效果一致的前提下，当然选择整体效果更优的$\theta _{2} $组模型。

在惩罚项前面还有一个$\alpha$系数，它表示正则化惩罚的力度。

如果$\alpha$值比较大，意味着要非常严格地对待权重参数，此时正则化惩罚的结果会对整体目标函数产生较大影响。

如果$\alpha$值比较小，意味着惩罚的力度较小，不会对结果产生太大影响。

 逻辑回归模型

参数对结果的影响

 

混淆矩阵

分类阈值对结果的影响