跟着迪哥学Python数据分析和机器学习(二）

回归算法

线性回归方程

$h_{\theta }(x) =\theta _{0} +\theta _{1}x_{1}+\theta _{2}x_{2}=\sum_{i=0}^{n}\theta _{i}x_{i}=\theta ^{T}x$

$\theta _{0}$为偏置项

误差项分析

误差项：真实值和预测值之间的差异。在样本中，每一个真实值和预测值之间都会存在一个误差

$y^{i} =\theta ^{T} x^{(i)}+\varepsilon ^{(i)}$

其中$i$为样本编号，$\theta ^{T} x^{(i)} $为预测值，$y^{i}$ 为真实值

误差$\varepsilon$是独立且具有相同的分布，并且服从均值为0方差为$\theta ^{2}$的高斯分布。

 　  相同分布是指符合同样的规则，即在相同银行的条件下来建立这个回归模型。

　　高斯分布用于描述正常情况下误差的状态。高斯分布也就是正态分布，是指数据正常情况下的样子。

　　　　高斯分布表达式为：$p^{(\varepsilon ^{(i)} )} =\frac{1}{\sqrt{2\pi } \sigma } exp(-\frac{(\varepsilon ^{(i)} )^{2} }{2\sigma^{2}  } )$

　　　　高斯分布图　

似然函数求解

将$y^{i} =\theta ^{T} x^{(i)}+\varepsilon ^{(i)}$代入高斯分布函数，可得

　　$p(y^{(i)}|x^{(i)};\theta ) =\frac{1}{\sqrt{2\pi } \sigma } exp(-\frac{(y^{i}-\theta ^{T} x^{(i)})^{2} }{2\sigma^{2} } )$

　　此函数的基本思路：找到最合适的参数来拟合数据点，可以把它当做是参数与数据组合后得到的跟标签值一样的可能性大小（如果预测值和标签值一模一样，那就做得很完美了）。对于这个可能性来说，大点好还是小点好呢？当然是大点好了，因为得到的预测值跟真实值越接近，意味着回归方程做得越好。所以就有了极大似然估计，找到最好的参数$\theta$，使其与$X$组合后能够成为$Y$的可能性越大越好。

似然函数定义：

　　$L(\theta)=\prod_{i=1}^{m} p(y^{(i)}|x^{(i)};\theta ) =\prod_{i=1}^{m} \frac{1}{\sqrt{2\pi } \sigma } exp(-\frac{(y^{i}-\theta ^{T} x^{(i)})^{2} }{2\sigma^{2} } )$

　　其中$i$为当前样本，$m$为整个数据集样本的个数

Notes:

　　建立的回归模型是满足部分样本点还是全部样本点呢？应该是尽可能满足数据集整体，所以需要考虑所有样本。那么如何解决乘法问题呢？一旦数据量较大，这个公式就会相当复杂，这就需要对似然函数进行对数变换，让计算简便一些。

如果对上述公式做变换，得到的结果值可能跟原来的目标值不一样了，但是在求解过程中希望得到极值点，非非极值，也就是能使$L(\theta)$越大的参数$\theta$，所以当进行变换操作时，保证极值点不变即可。

在对数中，可以将乘法转换成加法，即$log(A.B)=logA+logB$

对似然函数两边计算其对数结果可得：

　　$logL(\theta)=log\prod_{i=1}^{m} \frac{1}{\sqrt{2\pi } \sigma } exp(-\frac{(y^{i}-\theta ^{T} x^{(i)})^{2} }{2\sigma^{2} } )$

　　　　　　  $=\sum_{i=1}^{m} log\frac{1}{\sqrt{2\pi } \sigma } exp(-\frac{(y^{i}-\theta ^{T} x^{(i)})^{2} }{2\sigma^{2}  } )$

　　　　　　  $=mlog\frac{1}{\sqrt{2\pi } \sigma } -\frac{1}{\sigma} \times \frac{1}{2}\sum_{i=1}^{m} (y^{i}-\theta ^{T} x^{(i)})^{2}$

• 　　$log\frac{1}{\sqrt{2\pi } \sigma } $可以当做一个常数项，因为它与参数$\theta$没有关系。
• 　　对于$\frac{1}{\sigma} \times \frac{1}{2}\sum_{i=1}^{m} (y^{i}-\theta ^{T} x^{(i)})^{2}$来说，由于有平方项，其值必然恒为正。
• 　　整体来看就是要使得一个常数项减去一个恒正的公式的值越大越好，由于常数项不变，那就只能让$\frac{1}{\sigma} \times \frac{1}{2}\sum_{i=1}^{m} (y^{i}-\theta ^{T} x^{(i)})^{2}$越小越好，$\frac{1}{\sigma}$可以认为是一个常数，故只需让 $\frac{1}{2}\sum_{i=1}^{m} (y^{i}-\theta ^{T} x^{(i)})^{2}$越小越好，这就是最小二乘法。

线性回归求解

目标函数如下：

　　$J(\theta)= \frac{1}{2}\sum_{i=1}^{m} (h_{\theta }( x^{i})- y^{(i)})^{2}=\frac{1}{2}(X\theta -y)^{T}(X\theta -y) $

　　既然要求极值（使其得到最小值的参数$\theta $），对其计算其偏导数即可：

　　$\bigtriangledown _{\theta } J(\theta)= \bigtriangledown _{\theta }(\frac{1}{2}(X\theta -y)^{T}(X\theta -y))$

　　　　　　 $=\bigtriangledown _{\theta }(\frac{1}{2}(X^{T}\theta^{T} -y^{T})(X\theta -y)) $

　　　　　　 $=\bigtriangledown _{\theta }(\frac{1}{2}(X^{T}\theta^{T}X\theta-X^{T}\theta^{T}Xy -y^{T}X\theta -y^{T}y)) $

　　　　　　 $=\bigtriangledown _{\theta }(2X^{T}X\theta-X^{T}y-(y^{T}X)^{T})$

　　　　　　 $=X^{T}X\theta-X^{T}y=0$

　　　　　　 $\Rightarrow \theta=(X^{T}X)^{-1}X^{T}y$

 梯度下降算法

　　机器学习的核心思想就是不断优化寻找更合适的参数，当给定一个目标函数之后，自然就是想办法使真实值和预测值之间的差异越小越好。

　　下山问题：

　　　　为什么是下山呢？因为在这里把目标函数比作山，到底是上山还是下山，取决于你优化的目标是越大越好（上山）还是越小越好（下山），而基于最小二乘法判断是下山问题。

　　那该如何下山呢？有两个因素可控制——方向和步长。

下山方向选择:

　　首先需要明确的是什么方向能够使得下山最快。

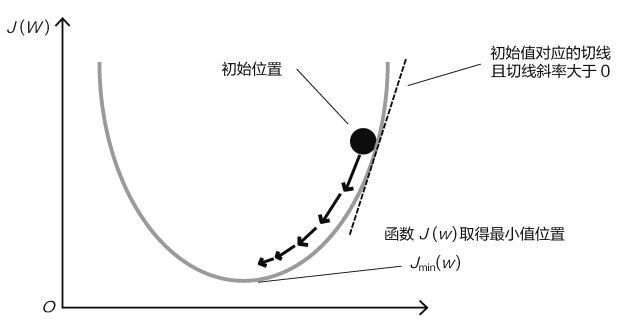
 　　梯度下降：当要求一个目标函数极值的时候，按照机器学习的思想直接求解看起来并不容易，可以逐步求其最优解。首先确定优化的方向（也就是梯度），再去实际走那么一步（也就是下降），反复执行这样的步骤，就慢慢完成了梯度下降任务，每次优化一点，累计起来就是一个大成绩。

梯度下降优化

目标函数:$J(\theta)= \frac{1}{2m}\sum_{i=1}^{m} (h_{\theta }( x^{i})- y^{(i)})^{2}$,目标就是找到最合适的参数$\theta$，使得目标函数值最小。这里x是数据，y是标签，都是固定的，所以只有参数$\theta$会对最终结果产生影响，此外，还需要注意参数$\theta$并不是一个值，可能是很多个参数共同决定了最终的结果。

 当进行优化的时候，该怎么处理这些参数呢？其中$\theta_{0} $与$\theta_{1} $分别和不同的数据特征进行组合（例如工资和年龄），按照之前的想法，既然$x_{1} $和$x_{2} $是相互独立的，那么在参数优化的时候自然需要分别考虑$\theta_{0} $和$\theta_{1} $的情况，在实际计算中，需要分别对$\theta_{0} $与$\theta_{1} $求偏导，再进行更新。

　　下面总结一下梯度下降算法：

　　 第①步：找到当前最合适的方向，对于每个参数都有其各自的方向。

　　 第②步：走一小步，走得越快，方向偏离越多，可能就走错路。

　　　　为什么是一小步呢？因为当前求得的方向只是瞬间最合适的方向，并不意味着这个方向一直都只正确的。

　　  第③步：按照方向和步伐去更新参数。

 　　 第④步：重复第1步~第3步。

梯度下降策略对比

假设目标函数仍然是:$J(\theta)= \frac{1}{2m}\sum_{i=1}^{m} (h_{\theta }( x^{i})- y^{(i)})^{2}$。

梯度下降算法中有3种常见的策略：批量梯度下降、随机梯度下降和小批量梯度下降。这3种策略的基本思想都是一致的，只是在计算过程中选择样本的数量有所不同。

（1）批量梯度下降

　　需要考虑所有的样本，每一次迭代优化计算在公式中都需要把所有的样本计算一遍。

　　优点：该方法容易得到最优解，因为每一次迭代的时候都会选择整体最优的方向。

　　缺点：如果样本数量大，就会导致迭代速度非常慢。

　　批量梯度下降的计算公式：

　　　　$\frac{\partial  J(\theta)}{\partial \theta_{j}} = -\frac{1}{m}\sum_{i=1}^{m} (h_{\theta }( x^{i})- y^{(i)})x_{j}^{(i)} =0\Rightarrow \theta_{j}=\theta_{j}+\alpha \frac{1}{m}\sum_{i=1}^{m} (y^{(i)}-h_{\theta }( x^{i}))x_{j}^{(i)} $

• 更新参数的时候取了一个负号：因为现在要求解的是一个下山问题，即沿着梯度的反方向去前进。
• $\frac{1}{m}$表示对所选择的样本求其平均损失
• $i$表示选择的样本数据
• $j$表示特征。例如$\theta_{j}$表示工资所对应的参数，在更新时数据也需选择工资这一列，这是一一对应的关系。
• 在更新时还涉及系数$\alpha$，其含义就是更新幅度的大小，也就是步长

（2）随机梯度下降

　　每次仅选择一个样本

　　优点：迭代速度会大大提升

　　缺点：不一定每次都朝着收敛的方向

　　随机梯度下降的计算公式：

　　　　$\theta_{j}=\theta_{j}+\alpha ( y^{(i)}-h_{\theta }( x^{i}))x_{j}^{(i)} $

　　与批量梯度下降的计算公式的区别仅在于选择样本数量

（3）小批量梯度下降——实际中最常使用的方法。

　　例如：选择10个样本数据进行更新的情况：

　　　　$\theta_{j}=\theta_{j}+\alpha\frac{1}{10}\sum_{k=i}^{i+9}   ( y^{(k)}-h_{\theta }( x^{k}))x_{j}^{(i)} $

　　通常会把样本个数叫做batch，在实际和硬件配置允许的条件下，尽可能选择更大的batch，这会是的迭代优化结果更好一些。

学习率对结果的影响

　　步长就是学习率（更新参数值的大小），通常都会选择较小的学习率，以及较多的迭代次数，正常的学习曲线走势如下：

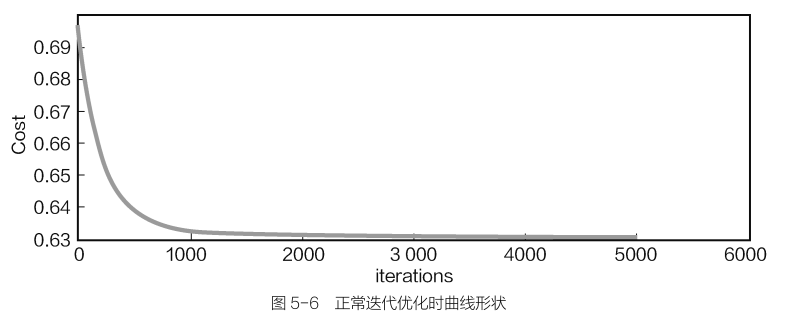
 　　随着迭代的进行，目标函数会逐渐降低，直到达到饱和收敛状态，这里只需观察迭代过程中曲线的形状变化，具体数值还是需要结合实际数据。

　　如果选择较大的学习率：学习过程可能会变得不平稳，因为这一步可能跨越太大了，偏离了正确的方向。

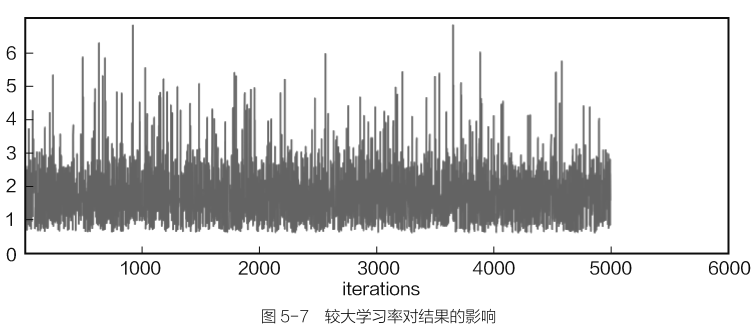
 　　在迭代过程中出现不平稳现象，目标函数始终没能达到收敛状态，甚至学习效果越来越差，这很可能是①学习率过大、②选择样本数据过小、③数据预处理问题所导致的。

　　如何选择合适的学习率　　

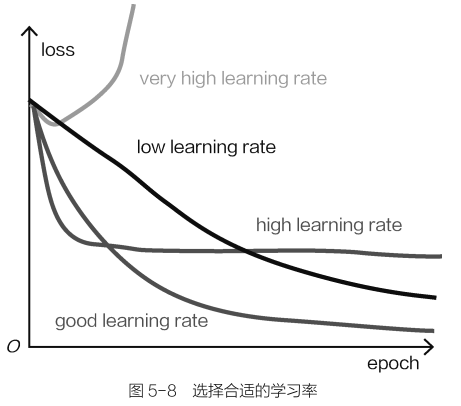
•  较大的学习率并不会使得目标函数降低，较小的学习率看起来还不错，可以选择较多的迭代次数来保证达到收敛状态。

逻辑回归算法

 　　逻辑回归算法并不是线性回归算法的升级，逻辑回归本质上是一个经典的二分类问题。

原理推导

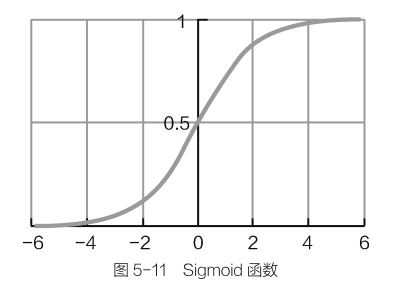
　　Sigmoid函数

　　　　定义如下：$g(z)=\frac{1}{1+e^{z} } $

　　　　在Sigmoid函数中，自变量$z$可以取任意实数，其结果值域为[0,1]，相当于输入一个任意大小的的分值，得到的结果都在[0,1]之间，恰好可以把它当作分类结果的概率值。

　　　　判断最终分类结果时，可以选择以0.5为阈值来进行正负例类别划分。

 　　逻辑回归计算流程：

　　　　①首先得到得分值；

　　　　②然后通过Sigmoid函数转换成概率值，公式如下：

　　　　　　$h_{\theta }(x) =g(\theta ^{T}x)= \frac{1}{1+e^{-\theta ^{T} x} } $

　　　　　　这个公式与线性回归方程有点相似，仅仅多了Sigmoid函数这一项

　　　　　　$x$依旧是特征数据

　　　　　　$\theta$依旧是每个特征对应的参数

　　下面对正例和负例情况分别进行分析

\begin{cases}
P(y=1|x;\theta )=h_{\theta }(x)
\\
P(y=0|x;\theta )=1-h_{\theta }(x)
\end{cases}

 　　　　当正例概率是$h_{\theta }(x)$时，负例概率必为$1-h_{\theta }(x)$

　　　当y=0时，$P(y=0|x;\theta )=(h_{\theta } (x))^{y} (1-h_{\theta } (x))^{1-y}=1-h_{\theta } (x)$

　　　当y=1时，$P(y|x;\theta )=(h_{\theta } (x))^{y} (1-h_{\theta } (x))^{1-y}=h_{\theta } (x)$

\begin{cases}
&P(y=1|x;\theta )=h_{\theta }(x) \\
&P(y=0|x;\theta )=1-h_{\theta }(x)
\end{cases}
　　　　   　　　　　　　　$\Rightarrow
P(y|x;\theta )=(h_{\theta } (x))^{y} (1-h_{\theta } (x))^{1-y}$

逻辑回归求解

　　首先得到似然函数：

　　　　$L(\theta )=\prod_{i=1}^{m} P(y_{i} |x_{i} ;\theta )=\prod_{i=1}^{m} (h_{\theta } (x_{i}))^{y_{i} } (1-h_{\theta (x_{i} }))^{1-yi }   $

　　对上式两边取对数，进行简化，结果如下：

　　　　$l(\theta )=log(L(\theta ))=\sum_{i=1}^{m} (y_{i} logh_{\theta }(x_{i})+(1-y_{i})log(1-h_{\theta }(x_{i})))$

　　此时，只需求目标函数的极小值，按照梯度下降的方法，照样去求偏导：

　　　　

 

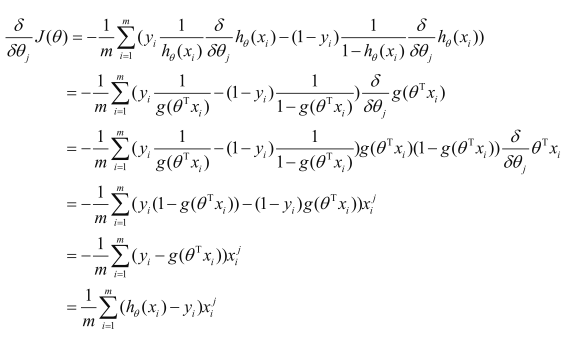
 　　　　$i$表示样本，也就是迭代过程中，选择的样本编号

　　　　 下标$j$表示特征编号，也就是参数编号，因为参数$\theta$和数据特征是一一对应的关系。

　　　　 对$\theta_{j}$求偏导，最后得到的结果也是乘以$x_{j}$，这表示要对哪个参数进行更新，需要用其对应的特征数据，而与其他特征无关。

　　　得到上面的偏导数后，就可以对参数进行更新，公式如下：

　　　　　$\theta_{j} =\theta_{j} -\alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta } (x_{i })-y_{i})x_{i}^{j}  $

　　　　　这样就得到了再逻辑回归中每一个参数该如何进行更新，求解方法依旧是迭代优化的思想。找到最合适的参数$\theta$，任务也就完成了。