[BZOJ2839] 集合计数
集合计数
题目描述
输入格式
输出格式
样例
数据范围与提示
首先先选出$k$个交集的元素，方案数为$C_n^k$；
然后已经选了$k$个元素，还剩下$n-k$个元素，那么共有$2^{n-k}$个集合可选。
那么我们从$2^{n-k}$个集合中选出i个集合的方案数为$C_{n-k}^i$。
总的方案数就是 $C_{2^{n-k}}^0+C_{2^{n-k}}^1+C_{2^{n-k}}^2+......+C_{2^{n-k}}^{2^{n-k}}$。
然后关键的就是一个公式 上面的式子就等于 $2^{2^{n-k}}$。
证明 参考 这里
其实也可以感性的理解一下，就是每个方案都有选和不选两种情况，乘法计数原理。
然后要想办法让剩下的方案里面没有交集才能满足条件。
关于容斥原理：
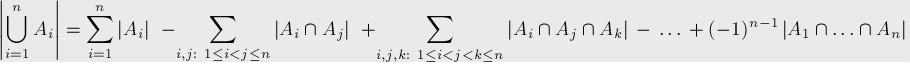
可以用递归的思想来证明，
首先我们要所有的加起来然后减去他们的交集，然后他们的交集中又有交集，所以可以接着减。
最后 $S=S_{所有}-S_{交集}$
$=S_{所有}-(S_{交集}-S_{交集的交集})$
$=......$
$=S-(S-(S-(......)))$。
最后去掉括号就是式子中的 系数。
当然也有更严谨的证明，可以在网上搜索一下。
然后就是这个题，
至于为什么要用容斥，这是个问题。。。
不能用 总的方案数直接减去交集大于等于$1$的方案数。
假设我们把这所有的方案分成几部分，有交集为$A$的，有交集为$B$的，有交集为$C$的，
之后$A$和$B$的交集为$AB$，$A$和$C$的交集为$AC$，$B$的$C$的交集为$BC$，$A$、$B$、$C$的交集为$ABC$。
那么也就很好理解这个题的容斥了。
如果我们用总方案数减去交集大于等于$1$的方案数，在维恩图中我们会看到多减了很多。
令$F_i=C_{n-k}^i \times (2^{2^{n-k-i}}-1)$。
这个含义就是我们已经选了$k$个元素作为交集，再选$i$个作为交集的方案数。
在这个式子中，肯定包含交集数$>i$的方案，所以说要用容斥。
我们要求的就是 所有交集数目$==0$的方案数。
我们只要用总方案数减去交集数$>=1$的方案的并集就可以。
最后那个$2^{2^{n-k-i}}$应该怎么算，可以用欧拉定理，算出$(2^{n-k-i})\%φ(mod)$。
然后算$2^{2^{n-k-i} \%φ(mod)} \%mod$。
#include<iostream>
#include<cstring>
#include<cstdio>
#define Reg register
#define mod 1000000007
#define Lucas(x,y) (jc[x]*ny[y]%mod*ny[x-y]%mod)
#define Ny(x) (Mi(x,mod-2,mod))
using namespace std;
long long ans,n,k,jc[1000050],ny[1000050];
long long Mi(long long x,long long y,long long p)
{
long long ans=1,base=x;
while(y)
{
if(y&1) ans=(ans*base)%p;
base=(base*base)%p;
y>>=1;
}
return ans;
}
long long Js(int x)
{
long long l1=Mi(2,x,mod-1);
long long ans=Mi(2,l1,mod);
ans=(ans+mod-1)%mod;
return ans;
}
void Jc(long long x)
{
jc[0]=ny[0]=1;
for(Reg int i=1;i<=x;++i)
{
jc[i]=(jc[i-1]*(i%mod))%mod;
ny[i]=Ny(jc[i]);
}
return;
}
int main()
{
scanf("%lld%lld",&n,&k);
Jc(n);
for(Reg int i=0,cur;i<=n-k;++i)
{
if((i&1)==0) cur=1;
else cur=-1;
long long q=(Lucas(n-k,i)*Js(n-i-k))%mod;
ans=(ans+mod+q*cur)%mod;
}
ans=(ans*Lucas(n,k))%mod;
printf("%lld",ans);
return 0;
}
