数据结构杂题
Trick
-
对于很难直接维护的修改,可以在上一次的答案上加上这次修改造成的贡献。(CF1928F Digital Patterns)
-
对于难维护的东西,可以考虑它的组合意义,变成 dp 问题,再用矩阵解决。(Distance)
-
对一个区间中的数去重后排序,可以考虑莫队。(Fibonacci-ish II)
-
快速维护斐波那契数列的变换,考虑用矩阵。(Fibonacci-ish II)
-
关于 \(\rm{mex}\) 的题目,可以考虑当 \(\rm{mex}\) 为 \(x\) 时的贡献。(Yet Another MEX Problem)
-
求 \(a_i\in[l,r]\) 的所有 \(a_i\) 的逆序对,可以令 \(id_{a_i}=i\),转化成求 \(i\in[l,r]\) 的 \(id_i\) 的逆序对。(Book Sorting)
-
对于两棵树换根的题目,考虑一棵树换根,另一棵树用数据结构维护在它与第一棵树的关系。(Two tree)
-
无向图,每次添加一条边。对于一条边,它能够出现在一个 SCC 中的时间是满足单调性的,所以可以用二分求出一条边出现 SCC 中的最小时间。(Simultaneous Coloring)
-
动态维护处理边的一些操作(改边权、删边、加边),可以考虑时间分治。([HNOI2010] 城市建设)
-
对于同时涉及位运算与加减的东西,考虑拆位维护每一位上的信息。(「FeOI Round 4.5」はぐ)
-
对于中位数的题目,考虑二分判定是否存在 \(\ge x\) 的中位数。(Big Wins!)
-
区间开根考虑势能线段树。(Farmer John's Favorite Function)
-
对于同时涉及位运算与加减的东西,考虑拆位维护每一位上的信息。(树锯解构)
-
当区间同时又包含与相交关系时,可以考虑之维护其中之一。(Building Forest Trails)
-
求的东西很难维护时,考虑拆贡献,然后对拆完的贡献逐项维护。(点心)
题目
Process with Constant Sum
中文题面:

这种题,先手玩一下样例。
然后就可以发现,不管怎么操作,最终得到的结果都一样,那么就考虑怎么快速模拟这个过程。
分析第一种操作,发现就是把当前数的值移动 \(2\) 到下一个数,那么一直做第一种操作,直到做不了为止,最后的序列满足除了最后一个数,剩下的数要么 \(0\) 要么 \(1\)。
这启发是可以给所有数值对 \(2\) 取模的。
然后再分析二操作,如果说对 1 0 1 操作,那么会得到 0 0 0(0 0 2 对 \(2\) 取模后就是 0 0 0);若对 1 0 0 操作,则会得到 1 0 1。
再手玩一下,就可以发现最后序列的形态一定为 0 0 0 ... 1 1 1 0/1,序列的最后一个数可以为 \(0\) 也可以为 \(1\)。
当然,除了最后一个数以外为 \(0\) 的地方,它不对 \(2\) 取模的值也肯定是 \(0\),对于最后一个数就不一定了。
所以这里只需要考虑最后一个位置的真实值,不难发现,如果初始序列有大于 \(1\) 的数,最后一个数就不可能是 \(0\);或者初始序列都小于等于 \(1\),那么也不能出现 1 0 1 这样的形式,因为这样会合成出一个 \(2\)。
所以,这个序列的初始值之和必须要等于最后的形态(也就是 0 0 0 ... 1 1 1 0/1)的和,才能确定最后一个数的真实值是否为 \(0\)。
现在考虑怎么快速模拟此操作,不难发现是可以放在线段树上搞的。
显然线段树上的一个区间所代表的形态肯定也形如 0 0 0 ... 1 1 1 0/1,那么就考虑如何合并两个区间。
如果两个区间 \(1\) 中间的 \(0\) 的个数为奇数,那么就会抵消 \(1\),也就是说对于 0 0 0 1 1 1 和 0 0 0 1 1 1 1 合并,最后的结果是 0 0 0 0 0 0 0 0 0 0 0 0 1。
如果两个区间 \(1\) 中间的 \(0\) 的个数为偶数,那么就会合并 \(1\),也就是说对于 0 0 0 1 1 1 和 0 0 1 1 1 1 合并,最后的结果是 0 0 0 0 0 1 1 1 1 1 1 1。
所以合并是可以 \(O(1)\) 做的,讨论一下即可。
代码
#include <bits/stdc++.h>
#define int long long
#define ls k << 1
#define rs k << 1 | 1
#define mid ((l + r) >> 1)
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n, q;
int a[N];
struct sgt {
int cnt, op, len, sum;
} tr[N * 4];
// cnt: 区间中 1 的个数;op: 区间的最后一个数是 0 还是 1;len: 区间长度;sum: 区间的初始值之和。
sgt merge( sgt a, sgt b) {
if ((a.op + b.len - b.cnt - b.op) % 2) {
if (b.cnt > a.cnt) return {b.cnt - a.cnt, b.op, a.len + b.len, a.sum + b.sum};
else if (b.cnt == a.cnt) return {0, 1, a.len + b.len, a.sum + b.sum};
else return {a.cnt - b.cnt, b.op ^ 1, a.len + b.len, a.sum + b.sum};
}
return {a.cnt + b.cnt, b.op, a.len + b.len, a.sum + b.sum};
}
void build( int k = 1, int l = 1, int r = n) {
if (l == r) {
if (a[l] % 2) tr[k] = {1, 0, 1, a[l]};
else tr[k] = {0, 1, 1, a[l]};
return ;
}
build(ls, l, mid), build(rs, mid + 1, r);
tr[k] = merge(tr[ls], tr[rs]);
}
void upd( int x, int v, int k = 1, int l = 1, int r = n) {
if (l == r) {
if (v % 2) tr[k] = {1, 0, 1, v};
else tr[k] = {0, 1, 1, v};
return ;
}
x <= mid ? upd(x, v, ls, l, mid) : upd(x, v, rs, mid + 1, r);
tr[k] = merge(tr[ls], tr[rs]);
}
sgt ask( int x, int y, int k = 1, int l = 1, int r = n) {
if (x <= l && r <= y) return tr[k];
if (y <= mid) return ask(x, y, ls, l, mid);
if (x > mid) return ask(x, y, rs, mid + 1, r);
return merge(ask(x, y, ls, l, mid), ask(x, y, rs, mid + 1, r));
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
for ( int i = 1; i <= n; i ++) cin >> a[i];
build(1, 1, n);
cin >> q;
while (q --) {
int op, l, r;
cin >> op >> l >> r;
if (op == 1) {
upd(l, r);
} else {
sgt res = ask(l, r);
cout << res.len - res.cnt - (res.op ? (res.sum > res.cnt ? 1 : 0) : 0) << '\n';
}
}
return 0;
}
CF1928F Digital Patterns
首先考虑一个合法的正方形是怎么出来的。
分析后发现,如果一个左上角为 \((x,y)\) 长度为 \(d\) 的正方形合法,只需要满足 \(i\in[x,x+d-1),a_i\neq a_{i+1}\) 且 \(j\in[y,y+d-1),b_j\neq b_{j+1}\) 即可。
然后考虑去维护极长的一个连续段 \(X\) 满足没有相邻的 \(a\) 相同,和极长连续段 \(Y\) 满足没有相邻的 \(b\) 相同。
假设 \(|X|\le |Y|\)(\(|X|\) 指连续段 \(X\) 的长度)。
那么这两个连续段对合法正方形的贡献记为 \(f(X,Y)\),就有:
这个式子显然可以化成只与 \(|X|\)、\(|Y|\) 有关的式子:
相当于知道 \(|X|\) 与 \(|Y|\) 后可以 \(O(1)\) 计算贡献。
那么现在考虑给 \(a\) 数组分成若干个极长连续段,记为 \(X_1\)、\(X_2\)、\(\dots\)、\(X_p\)。
同理把 \(b\) 也分成若干极长连续段,记为 \(Y_1\)、\(Y_2\)、\(\dots\)、\(Y_q\)。
如何维护连续段?差分以后,两个 \(0\) 之间就是一个连续段,用 set 维护这些 \(0\) 的位置即可。
为了简化式子,再记 \(u(i)=i\)、\(v(i)=\frac{i(i+1)}{2}\)、\(w(i)=\frac{i(i+1)(2i+1)}{6}-\frac{i^2(i+1)}{2}\)。
那么最后求的就是:
化到最简就是:
维护这个东西,可以在修改之前先求一遍答案,然后考虑修改会造成的影响。
以修改 \(a\) 数组为例,没次修改只会使极长连续段的个数造成 \(O(1)\) 的变化,那么直接 set 里面改就行,计算贡献时用一个树状数组来处理形如这样 \(\sum_{Y_j\ge X_i}\) 的贡献。
修改 \(b\) 数组与修改 \(a\) 数组同理。
代码
#include <bits/stdc++.h>
#define int long long
void Freopen() {
freopen(".in", "r", stdin);
freopen(".out", "w", stdout);
}
using namespace std;
const int N = 3e5 + 10, M = 2e5 + 10, inf = 1e16, mod = 998244353;
int n, m, q;
int a[N], b[N], da[N], db[N];
int u( int i) {
return i;
}
int v( int i) {
return i * (i + 1) / 2;
}
int w ( int i) {
return i * (i + 1) * (2 * i + 1) / 6 - i * i * (i + 1) / 2;
}
struct bit {
int tr[N], n;
void add( int u, int v) {
if (u <= 0) return ;
for (; u <= n; u += (u & -u)) tr[u] += v;
}
int ask( int u, int res = 0) {
if (u <= 0) return 0;
if (u > n) u = n;
for (; u; u -= (u & -u)) res += tr[u];
return res;
}
} ;
bit y, yu, yw, yv, x, xu, xw, xv;
void addx( int k, int op) {
x.add(n - k + 1, op), xu.add(n - k + 1, u(k) * op);
xw.add(k, w(k) * op), xv.add(k, v(k) * op);
}
void addy( int k, int op) {
y.add(m - k + 1, op), yu.add(m - k + 1, u(k) * op);
yw.add(k, w(k) * op), yv.add(k, v(k) * op);
}
int askx( int k) {
return w(k) * x.ask(n - k + 1) + v(k) * xu.ask(n - k + 1) + xw.ask(k - 1) + u(k) * xv.ask(k - 1);
}
int asky( int k) {
return w(k) * y.ask(m - k + 1) + v(k) * yu.ask(m - k + 1) + yw.ask(k - 1) + u(k) * yv.ask(k - 1);
}
set< int> s1, s2;
int ans = 0;
void upd1( int k, int x) {
if (k == n + 1) return ;
if (! da[k] && da[k] + x) {
auto it = s1.find(k), pre = prev(it), nxt = next(it);
addx(* it - * pre, -1), ans -= asky(* it - * pre);
addx(* nxt - * it, -1), ans -= asky(* nxt - * it);
addx(* nxt - * pre, 1), ans += asky(* nxt - * pre);
s1.erase(it);
}
if (da[k] && ! (da[k] + x)) {
auto it = s1.insert(k).first, pre = prev(it), nxt = next(it);
addx(* nxt - * pre, -1), ans -= asky(* nxt - * pre);
addx(* it - * pre, 1), ans += asky(* it - * pre);
addx(* nxt - * it, 1), ans += asky(* nxt - * it);
}
da[k] += x;
}
void upd2( int k, int x) {
if (k == m + 1) return ;
if (! db[k] && db[k] + x) {
auto it = s2.find(k), pre = prev(it), nxt = next(it);
addy(* it - * pre, -1), ans -= askx(* it - * pre);
addy(* nxt - * it, -1), ans -= askx(* nxt - * it);
addy(* nxt - * pre, 1), ans += askx(* nxt - * pre);
s2.erase(it);
}
if (db[k] && ! (db[k] + x)) {
auto it = s2.insert(k).first, pre = prev(it), nxt = next(it);
addy(* nxt - * pre, -1), ans -= askx(* nxt - * pre);
addy(* it - * pre, 1), ans += askx(* it - * pre);
addy(* nxt - * it, 1), ans += askx(* nxt - * it);
}
db[k] += x;
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m >> q;
a[0] = b[0] = inf;
y.n = yu.n = yw.n = yv.n = m;
x.n = xu.n = xw.n = xv.n = n;
for ( int i = 1; i <= n; i ++)
cin >> a[i], da[i] = a[i] - a[i - 1];
for ( int i = 1; i <= m; i ++)
cin >> b[i], db[i] = b[i] - b[i - 1];
s1.insert(1), s2.insert(1), s1.insert(n + 1), s2.insert(m + 1);
for ( int i = 1; i <= n; i ++) if (da[i] == 0) s1.insert(i);
for ( int i = 1; i <= m; i ++) if (db[i] == 0) s2.insert(i);
for ( auto it = s1.begin(); next(it) != s1.end(); it ++) addx(* next(it) - * it, 1);
for ( auto it = s2.begin(); next(it) != s2.end(); it ++) addy(* next(it) - * it, 1);
for ( auto it = s1.begin(); next(it) != s1.end(); it ++)
ans += asky(* next(it) - * it);
cout << ans << '\n';
while (q --) {
int op, l, r, x;
cin >> op >> l >> r >> x;
if (op == 1) upd1(l, x), upd1(r + 1, -x);
if (op == 2) upd2(l, x), upd2(r + 1, -x);
cout << ans << '\n';
}
return 0;
}
Distance
没有原题。

\(n,q\le3\times 10^5\)。
考虑这个询问怎么刻画。
枚举路径 \(x\to y\) 上的点 \(z\),让 \(z\) 成为 \(x\)、\(y\) 的 \(lca\)。
那么当 \(z\) 为 \(lca\) 时,贡献就是 \((\sum_{e\in x\to z}W_e)(S_z)(\sum_{e\in z\to y}W_e)\)(\(W_e\) 表示边 \(e\) 的权值,\(S_z\) 表示不经过路径能够到达点 \(z\) 的点的数量)。
如果把 \(S\) 看作点的点权,那么它的组合意义就是在路径上有顺序地选择一条边、一个点、一条边,把它们权值乘起来的和。
这似乎可以 dp,考虑在序列上怎么求。
设 \(f_{i,0/1/2}\) 表示选了一条边/一条边、一个点/一条边、一个点、一条边的权值乘积之和,转移就是 \(O(1)\) 合并。
这启发可以放在矩阵上转移,然后树剖维护。
但是现在有些细节的问题,就比如 \(S_u\) 怎么处理?因为不同的路径 \(S_u\) 的值不一样。
可以这样考虑,把 \(S_{fa_u}\) 的值挂在 \(u\) 上,这样 \(S_{fa_u}\) 的值唯一,也就是 \(siz_{fa_u}-siz_u\),同时把 \((fa_u,u)\) 这条边的权值挂在 \(u\) 上。
当然,对于路径的 \(lca\) 是特殊情况,因为 \(S_{lca}\) 是 \(n\) 减去 \(lca\) 在路径上的两个儿子的子树大小,所以考虑把 \(lca\) 的矩阵单独处理出来。
还有些细节,比如说线段树合并的方向,树剖重链合并的方向都要注意。
当然 \(\log^2\) 加上矩阵乘法的复杂度是很高的,所以考虑只维护矩阵会改变的位置(上三角),一共只有 \(6\) 个位置,可以看作 \(O(1)\)。
代码
#include <bits/stdc++.h>
#define int unsigned int
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 3e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n, q;
vector< pair< int, int> > G[N];
int W[N];
int dep[N], siz[N], fa[N], son[N];
int top[N], dfn[N], rev[N];
int tot;
void dfs1( int u, int fu) {
fa[u] = fu, siz[u] = 1, dep[u] = dep[fu] + 1;
for ( auto [v, w] : G[u]) {
if (v == fu) continue ;
dfs1(v, u);
W[v] = w, siz[u] += siz[v];
son[u] = (siz[v] > siz[son[u]] ? v : son[u]);
}
}
void dfs2( int u, int topt) {
top[u] = topt, dfn[u] = ++ tot, rev[tot] = u;
if (son[u]) dfs2(son[u], topt);
for ( auto [v, w] : G[u])
if (v != fa[u] && v != son[u])
dfs2(v, v);
}
int lca( int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
u = fa[top[u]];
}
return dep[u] < dep[v] ? u : v;
}
int Kth( int u, int k) {
while (dep[u] - dep[top[u]] + 1 <= k) {
k -= (dep[u] - dep[top[u]] + 1);
u = fa[top[u]];
}
return rev[dfn[u] - k];
}
struct mat {
int a[6];
void reset() {
for ( int i = 0; i < 6; i ++)
a[i] = 0;
}
mat operator * ( const mat & x) const {
mat z;
z.a[0] = a[0] + x.a[0];
z.a[1] = x.a[1] + a[0] * x.a[3] + a[1];
z.a[2] = x.a[2] + x.a[4] * a[0] + x.a[5] * a[1] + a[2];
z.a[3] = x.a[3] + a[3];
z.a[4] = x.a[4] + a[3] * x.a[5] + a[4];
z.a[5] = x.a[5] + a[5];
return z;
}
} ;
void tag( mat & a, int u, int op) {
a.reset();
int S = siz[fa[u]] - siz[u];
a.a[0] = a.a[5] = W[u];
a.a[3] = S;
if (! op) a.a[1] = W[u] * S;
else a.a[4] = W[u] * S;
}
struct sgt {
mat tr[2][N * 4];
#define ls k << 1
#define rs k << 1 | 1
#define mid ((l + r) >> 1)
void psu( int k) {
tr[0][k] = tr[0][rs] * tr[0][ls];
tr[1][k] = tr[1][ls] * tr[1][rs];
}
void build( int k = 1, int l = 1, int r = n) {
tr[0][k].reset(), tr[1][k].reset();
if (l == r) {
tag(tr[0][k], rev[l], 0);
tag(tr[1][k], rev[l], 1);
return ;
}
build(ls, l, mid), build(rs, mid + 1, r);
psu(k);
}
void upd( int x, int w, int k = 1, int l = 1, int r = n) {
if (l == r) {
W[rev[l]] = w;
tag(tr[0][k], rev[l], 0);
tag(tr[1][k], rev[l], 1);
return ;
}
x <= mid ? upd(x, w, ls, l, mid) : upd(x, w, rs, mid + 1, r);
psu(k);
}
mat ask( int x, int y, int op, int k = 1, int l = 1, int r = n) {
if (x <= l && r <= y) return tr[op][k];
if (y <= mid) return ask(x, y, op, ls, l, mid);
if (x > mid) return ask(x, y, op, rs, mid + 1, r);
return (op ?
ask(x, y, op, ls, l, mid) * ask(x, y, op, rs, mid + 1, r) :
ask(x, y, op, rs, mid + 1, r) * ask(x, y, op, ls, l, mid));
}
#undef ls
#undef rs
#undef mid
} T;
mat ask( int u, int v, int op) {
mat res;
res.reset();
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
res = (op ? T.ask(dfn[top[u]], dfn[u], op) * res : res * T.ask(dfn[top[u]], dfn[u], op));
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
res = (op ? T.ask(dfn[v], dfn[u], op) * res : res * T.ask(dfn[v], dfn[u], op));
return res;
}
struct edge {
int u, v;
} E[N];
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> q;
for ( int i = 1; i < n; i ++) {
int u, v, w; cin >> u >> v >> w;
G[u].push_back({v, w});
G[v].push_back({u, w});
E[i] = {u, v};
}
dfs1(1, 0), dfs2(1, 1);
T.build();
for ( int i = 1; i < n; i ++)
if (dep[E[i].u] < dep[E[i].v]) swap(E[i].u, E[i].v);
while (q --) {
int op, x, y; cin >> op >> x >> y;
if (op == 1) T.upd(dfn[E[x].u], y);
else {
if (x == y) {
cout << 0 << '\n';
continue ;
}
int lca = :: lca(x, y);
mat ans;
ans.reset();
if (y == lca) {
int u = Kth(x, dep[x] - dep[lca] - 1);
ans = ans * ask(x, u, 0);
cout << ans.a[2] << '\n';
continue ;
}
if (x == lca) {
int v = Kth(y, dep[y] - dep[lca] - 1);
ans = ans * ask(y, v, 1);
cout << ans.a[2] << '\n';
continue ;
}
mat L;
int u = Kth(x, dep[x] - dep[lca] - 1);
int v = Kth(y, dep[y] - dep[lca] - 1);
int S = n - siz[u] - siz[v];
L.a[0] = L.a[5] = W[u] + W[v];
L.a[1] = W[u] * S;
L.a[2] = W[u] * W[v] * S;
L.a[4] = W[v] * S;
L.a[3] = S;
if (dep[x] - dep[lca] >= 2) {
int X = Kth(x, dep[x] - dep[lca] - 2);
ans = ans * ask(x, X, 0);
}
ans = ans * L;
if (dep[y] - dep[lca] >= 2) {
int Y = Kth(y, dep[y] - dep[lca] - 2);
ans = ans * ask(y, Y, 1);
}
cout << ans.a[2] << '\n';
}
}
return 0;
}
Fibonacci-ish II
对于去重排序的询问,考虑莫队。
那重点是当插入一个数时,贡献会如何变化。
主要问题是斐波那契数列的项数很难表示,所以考虑用矩阵来处理。
斐波那契数列有:
所以可以给每个数维护一个矩阵,假设这个数为 \(x\),那么它对应的矩阵就可以是 \(\begin{bmatrix} x\times f_{i-1} & x\times f_i \end{bmatrix}\)。
当插入一个数的时候,先看一下它前面有多少个数,算出 \(\begin{bmatrix} f_{i-1} & f_i \end{bmatrix}\) 的值,然后把在它后面的数的矩阵都乘上 \(\begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix}\),这可以用权值线段树做。
对于删除,因为矩阵 \(\begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix}\) 有逆,所以也可做。
复杂度 \(O(n\sqrt{n}\log n)\)。
很神秘的是手动维护矩阵还是过不了,不想卡常了。
代码
#include <iostream>
#include <algorithm>
#include <math.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 3e4 + 10, M = 2e5 + 10, inf = 1e9;
int n, m, mod, blk;
int a[N], ind[N], f[N], ans[N];
int tot;
int L = 1, R;
struct que {
int l, r, id;
bool operator < ( const que & rhs) const {
return (l / blk == rhs.l / blk) ? ((l / blk) & 1 ? r < rhs.r : r > rhs.r) : l < rhs.l;
}
} q[N];
int add( int x, int v) {
x += v;
return x >= mod ? x - mod : x;
}
struct mat {
int a00, a01, a10, a11;
void reset() {
a00 = a01 = a10 = a11 = 0;
}
void init() {
a00 = a11 = 1, a01 = a10 = 0;
}
mat operator * ( const mat & x) const {
mat z;
z.a00 = (a00 * x.a00 + a01 * x.a10) % mod;
z.a01 = (a00 * x.a01 + a01 * x.a11) % mod;
z.a10 = (a10 * x.a00 + a11 * x.a10) % mod;
z.a11 = (a10 * x.a01 + a11 * x.a11) % mod;
return z;
}
mat operator + ( const mat & x) const {
mat z;
z.a00 = add(a00, x.a00);
z.a01 = add(a01, x.a01);
z.a10 = add(a10, x.a10);
z.a11 = add(a11, x.a11);
return z;
}
} ;
mat A, B;
struct sgt {
#define ls k << 1
#define rs k << 1 | 1
#define mid ((l + r) >> 1)
int sum[N * 4];
mat tr[N * 4], lz[N * 4];
void build( int k = 1, int l = 1, int r = tot) {
tr[k].reset();
lz[k].init();
if (l == r) return ;
build(ls, l, mid), build(rs, mid + 1, r);
}
void psu( int k) {
tr[k] = tr[ls] + tr[rs];
sum[k] = sum[ls] + sum[rs];
}
void pst( int k, const mat & v) {
tr[k] = tr[k] * v;
lz[k] = lz[k] * v;
}
void psd( int k) {
if (lz[k].a00 == 1 && lz[k].a11 == 1 && lz[k].a01 == 0 && lz[k].a10 == 0) return ;
pst(ls, lz[k]), pst(rs, lz[k]);
lz[k].init();
}
void insert( int x, int v, int id, int k = 1, int l = 1, int r = tot) {
if (l == r) {
sum[k] += v;
if (id) {
tr[k].a00 = f[id - 1] * ind[x] % mod;
tr[k].a01 = f[id] * ind[x] % mod;
} else tr[k].a00 = tr[k].a01 = 0;
return ;
}
psd(k);
x <= mid ? insert(x, v, id, ls, l, mid) : insert(x, v, id, rs, mid + 1, r);
psu(k);
}
void upd( int x, int y, const mat & v, int k = 1, int l = 1, int r = tot) {
if (x > y) return ;
if (x <= l && r <= y) return pst(k, v);
psd(k);
if (x <= mid) upd(x, y, v, ls, l, mid);
if (y > mid) upd(x, y, v, rs, mid + 1, r);
psu(k);
}
int ask( int x, int y, int k = 1, int l = 1, int r = tot) {
if (x > y) return 0;
if (x <= l && r <= y) return sum[k];
psd(k);
int res = 0;
if (x <= mid) res += ask(x, y, ls, l, mid);
if (y > mid) res += ask(x, y, rs, mid + 1, r);
return res;
}
#undef ls
#undef rs
#undef mid
} T;
int cnt[N];
void add( int x) {
cnt[x] ++;
if (cnt[x] != 1) return ;
int res = T.ask(1, x - 1) + 1;
T.insert(x, 1, res);
T.upd(x + 1, tot, A);
}
void del( int x) {
cnt[x] --;
if (cnt[x] != 0) return ;
T.insert(x, -1, 0);
T.upd(x + 1, tot, B);
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> mod;
blk = sqrt(n);
A.a00 = 0;
A.a01 = A.a10 = A.a11 = 1;
B.a00 = mod - 1;
B.a01 = B.a10 = 1;
B.a11 = 0;
f[1] = f[2] = 1;
for ( int i = 3; i <= n; i ++) f[i] = add(f[i - 1], f[i - 2]);
for ( int i = 1; i <= n; i ++) cin >> a[i], ind[i] = a[i];
sort(ind + 1, ind + n + 1), tot = unique(ind + 1, ind + n + 1) - ind - 1;
for ( int i = 1; i <= n; i ++) a[i] = lower_bound(ind + 1, ind + tot + 1, a[i]) - ind;
for ( int i = 1; i <= n; i ++) ind[i] %= mod;
T.build();
cin >> m;
for ( int i = 1; i <= m; i ++) {
int l, r; cin >> l >> r;
q[i] = {l, r, i};
}
sort(q + 1, q + m + 1);
for ( int i = 1; i <= m; i ++) {
int l = q[i].l, r = q[i].r, id = q[i].id;
while (R < r) add(a[++ R]);
while (L > l) add(a[-- L]);
while (R > r) del(a[R --]);
while (L < l) del(a[L ++]);
ans[id] = T.tr[1].a01;
}
for ( int i = 1; i <= m; i ++) cout << ans[i] << '\n';
return 0;
}
Yet Another MEX Problem
可以发现,对于一个区间,如果取的数不是 \(\rm{mex}\),而是任意一个没出现的数,那么求出来的贡献肯定小于等于取 \(\rm{mex}\) 时的答案。
这启发可以对 \(0\sim n\) 中的所有数求出取它的时候的贡献,取最大值就是答案。
那么考虑维护一个数组 \(f_x\),表示取 \(x\) 时,\(lst_x+1\sim r\) 中比 \(x\) 大的数的个数(\(lst_x\) 表示 \(x\) 最后一次出现的位置)。
初始 \(f_x=0\),每当 \(r\) 向右移动时,会添加 \(a_r\) 这个数,\(a_r\) 会给 \(0\sim a_r-1\) 中的 \(f_x\) 都 \(+1\),然后将 \(f_{a_r}\leftarrow 0\),最后询问 \(\max_{x=0}^n f_x\) 即可。
发现这就是前缀加、单点改、全局查询最大值,直接线段树即可。
代码
#include <bits/stdc++.h>
#define ls k << 1
#define rs k << 1 | 1
#define mid ((l + r) >> 1)
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 3e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n;
int a[N], lst[N];
int mx[N * 4], lz[N * 4];
void build( int k, int l, int r) {
mx[k] = lz[k] = 0;
if (l == r) return ;
build(ls, l, mid), build(rs, mid + 1, r);
}
void pst( int k, int v) {
mx[k] += v, lz[k] += v;
}
void psu( int k) {
mx[k] = max(mx[ls], mx[rs]);
}
void psd( int k) {
if (! lz[k]) return ;
pst(ls, lz[k]), pst(rs, lz[k]);
lz[k] = 0;
}
void upd( int x, int k = 1, int l = 0, int r = n) {
if (l == r) return mx[k] = 0, void();
psd(k);
x <= mid ? upd(x, ls, l, mid) : upd(x, rs, mid + 1, r);
psu(k);
}
void mdf( int x, int y, int k = 1, int l = 0, int r = n) {
if (x > y) return ;
if (x <= l && r <= y) return pst(k, 1);
psd(k);
if (x <= mid) mdf(x, y, ls, l, mid);
if (y > mid) mdf(x, y, rs, mid + 1, r);
psu(k);
}
void solve() {
cin >> n;
build(1, 0, n);
for ( int i = 1; i <= n; i ++) {
int x; cin >> x;
mdf(0, x - 1), upd(x);
cout << mx[1] << ' ';
}
cout << '\n';
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T; cin >> T;
while (T --) solve();
return 0;
}
Book Sorting
中文题面:
给出一个长为 \(n\) 的排列。每一次可以选择以下的任一操作进行:
- 交换相邻的两个数
- 将排列中一个数挪到序列开头
- 将排列中一个数挪到序列结尾
求使得排列有序的最小总操作次数。
\(n\le 5\times 10^5\)。
可以先分析一下操作大概会是什么样的,不难发现,对于每个数只会做 \(2\)、\(3\) 中的一个,且只会做一次。
那么可以想到最终的操作形式是,对值域在 \([1,x]\) 内的数做 \(2\) 操作,对值域在 \([y,n]\) 内的数做 \(3\) 操作,对值域在 \((x,y)\) 内的数做 \(1\) 操作。
然后发现,对 \((x,y)\) 内的数做一操作的次数,等于值域在 \((x,y)\) 内的数的逆序对个数。
由于值域上的逆序对很难求,希望能够放在序列上求,所以考虑令 \(id_{a_i}=i\),这样就可以把值域在 \([l,r]\) 内的数的逆序对转化成下标在 \([l,r]\) 内的数的逆序对。
打个表后能发现,对于 \(x\),它最优的 \(y\) 满足单调性,这启发可以分治处理。
然后维护序列的逆序对,使用树状数组即可。
代码
#include <bits/stdc++.h>
#define int long long
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 5e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n, ans = inf;
int a[N], p[N];
int L = 1, R = 0;
int tr1[N], tr2[N];
void add1( int u, int v) {
for (; u <= n; u += (u & -u)) tr1[u] += v;
}
void add2( int u, int v) {
for (; u; u -= (u & -u)) tr2[u] += v;
}
int ask1( int u, int res = 0) {
for (; u; u -= (u & -u)) res += tr1[u];
return res;
}
int ask2( int u, int res = 0) {
for (; u <= n; u += (u & -u)) res += tr2[u];
return res;
}
int now;
int cal( int l, int r) {
if (l > r) return 0;
if (R < l || L > r) {
for ( int i = L; i <= R; i ++) add1(p[i], -1), add2(p[i], -1);
now = 0;
for ( int i = l; i <= r; i ++) now += ask2(p[i]), add1(p[i], 1), add2(p[i], 1);
L = l, R = r;
return now;
}
while (R < r) R ++, now += ask2(p[R]), add1(p[R], 1), add2(p[R], 1);
while (L > l) L --, now += ask1(p[L]), add1(p[L], 1), add2(p[L], 1);
while (R > r) add1(p[R], -1), add2(p[R], -1), now -= ask2(p[R]), R --;
while (L < l) add1(p[L], -1), add2(p[L], -1), now -= ask1(p[L]), L ++;
return now;
}
void solve( int l, int r, int ql, int qr) {
if (l > r) return ;
int mid = (l + r) >> 1;
int mi = inf, qmid = 0;
for ( int i = max(mid + 1, ql); i <= qr; i ++) {
int res = mid + cal(mid + 1, i - 1) + (n - i + 1);
if (mi > res) mi = res, qmid = i;
}
ans = min(ans, mi);
solve(l, mid - 1, ql, qmid);
solve(mid + 1, r, qmid, qr);
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
for ( int i = 1; i <= n; i ++) cin >> a[i];
for ( int i = 1; i <= n; i ++) p[a[i]] = i;
solve(0, n + 1, 0, n + 1);
cout << ans << '\n';
return 0;
}
Two tree
中文题面:
记 \(F_{1/2,u,v}\) 表示在第 \(1/2\) 棵树上,当 \(u\) 为根时,\(v\) 的子树大小。
对于所有 \(u\),求出有多少 \(v\),满足 \(F_{1,u,v}\gt F_{2,u,v}\)。
既然对于所有根都要求答案,自然想到换根,所以先对每棵树都是 \(1\) 为根时求一遍子树大小。
显然这里不能两棵树同时换根,所以考虑对第一棵树换根,这样就可以得到第一棵树的所有点的子树大小,记为 \(siz1\)。
考虑在第二棵树上,把 \(u\) 变成根后有什么影响。
发现只有在 \(u\to 1\) 这条链上的所有点的子树大小会改变,除了点 \(u\)(点 \(u\) 为根时子树大小肯定是 \(n\)),其余点的子树大小为 \(n\) 减去它在链上的儿子的子树大小。
如何维护这个东西呢?不妨考虑用重链剖分,记 \(val_u\) 为 \(n\) 减去 \(u\) 的重儿子的子树大小,对于重链直接线段树维护 \(siz1_u\gt val_u\) 的个数,对于轻边单独判断即可。
因为链上只会有最多 \(O(\log n)\) 条轻边,所以复杂度 \(O(n\log^2 n)\)。
但是会发现这样做有点问题,可能会有:“换根前就大于,换根后也大于。”的情况,这样答案会多统计一次。
记第二棵树的点的子树大小为 \(siz2\),每次再减去 \(siz1\gt siz2\) 的个数就行了,这个再开一棵线段树维护即可。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 5e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n;
vector< int> G1[N];
vector< int> G2[N];
int siz1[N], fa1[N];
void dfs( int u, int fu) {
siz1[u] = 1, fa1[u] = fu;
for ( auto v : G1[u]) {
if (v == fu) continue ;
dfs(v, u);
siz1[u] += siz1[v];
}
}
int siz2[N], fa2[N], son[N];
void dfs1( int u, int fu) {
siz2[u] = 1, fa2[u] = fu;
for ( auto v : G2[u]) {
if (v == fu) continue ;
dfs1(v, u);
siz2[u] += siz2[v];
son[u] = (siz2[v] > siz2[son[u]] ? v : son[u]);
}
}
int tot;
int top[N], dfn[N], rev[N];
void dfs2( int u, int topt) {
top[u] = topt, dfn[u] = ++ tot, rev[tot] = u;
if (son[u]) dfs2(son[u], topt);
for ( auto v : G2[u])
if (v != son[u] && v != fa2[u])
dfs2(v, v);
}
struct sgt {
#define ls k << 1
#define rs k << 1 | 1
#define mid ((l + r) >> 1)
int sum[N * 4], val[N * 4];
void build( int op, int k = 1, int l = 1, int r = n) {
sum[k] = 0;
if (l == r) {
val[rev[l]] = (op ? siz2[rev[l]] : (n - siz2[son[rev[l]]]));
sum[k] = (siz1[rev[l]] > val[rev[l]]);
return ;
}
build(op, ls, l, mid), build(op, rs, mid + 1, r);
sum[k] = sum[ls] + sum[rs];
}
void upd( int x, int v, int k = 1, int l = 1, int r = n) {
if (l == r) return sum[k] = (v > val[rev[l]]), void();
x <= mid ? upd(x, v, ls, l, mid) : upd(x, v, rs, mid + 1, r);
sum[k] = sum[ls] + sum[rs];
}
int ask( int x, int y, int k = 1, int l = 1, int r = n) {
if (x > y) return 0;
if (x <= l && r <= y) return sum[k];
int res = 0;
if (x <= mid) res += ask(x, y, ls, l, mid);
if (y > mid) res += ask(x, y, rs, mid + 1, r);
return res;
}
} T0, T1;
int ans[N], SUM;
void DP( int u) {
ans[u] = SUM;
int x = u;
while (x) {
ans[u] += T0.ask(dfn[top[x]], dfn[x] - 1);
if (fa2[top[x]]) ans[u] += (siz1[fa2[top[x]]] > n - siz2[top[x]]);
ans[u] -= T1.ask(dfn[top[x]], dfn[x]);
x = fa2[top[x]];
}
int sizu = siz1[u], sum = SUM;
for ( auto v : G1[u]) {
if (v == fa1[u]) continue ;
int sizv = siz1[v];
SUM -= (siz1[u] > siz2[u]), SUM -= (siz1[v] > siz2[v]);
siz1[u] = n - siz1[v], siz1[v] = n;
T0.upd(dfn[u], siz1[u]), T1.upd(dfn[u], siz1[u]);
T0.upd(dfn[v], siz1[v]), T1.upd(dfn[v], siz1[v]);
SUM += (siz1[u] > siz2[u]), SUM += (siz1[v] > siz2[v]);
DP(v);
siz1[u] = sizu, siz1[v] = sizv, SUM = sum;
T0.upd(dfn[u], siz1[u]), T1.upd(dfn[u], siz1[u]);
T0.upd(dfn[v], siz1[v]), T1.upd(dfn[v], siz1[v]);
}
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
for ( int i = 1, u, v; i < n; i ++) {
cin >> u >> v;
G1[u].push_back(v);
G1[v].push_back(u);
}
for ( int i = 1, u, v; i < n; i ++) {
cin >> u >> v;
G2[u].push_back(v);
G2[v].push_back(u);
}
dfs(1, 0);
dfs1(1, 0), dfs2(1, 1);
T0.build(0), T1.build(1);
for ( int i = 1; i <= n; i ++) SUM += (siz1[i] > siz2[i]);
DP(1);
for ( int i = 1; i <= n; i ++) cout << ans[i] << ' ';
return 0;
}
Simultaneous Coloring
首先分析操作,不难发现只有最后一次操作有用。
那么对于 \(R\) 的限制,肯定先涂列,再涂行,\(B\) 就是反过来。
考虑把图建出来,\((x,y)\) 为 \(R\),就连 \((y+n,x)\),如果是 \(B\) 就连 \((x,y+n)\)。
然后发现建出来的图如果是 DAG,花费就是 \(0\),如果出现了环,就需要选择这个环的所有点,花费是环的点数的平方。
也就说答案等于图上所有 SCC 的点数平方和。
那么就把问题转化成动态加边,维护 SCC 的点数。
考虑一条边 \(i\) 能够出现在 SCC 中的一个最小时间 \(t_i\),这个 \(t_i\) 是有单调性的。
那么可以对所有边二分出来这个 \(t_i\)。(具体就是把 \([1,mid]\) 的边给建图,然后看这条边的两个端点是否在一个连通块里。)
求出 \(t_i\) 后,顺序遍历一遍时间,在对应时间把边加进并查集里,维护一下答案即可。
这样复杂度是 \(O(q(n+m)\log q)\),因为要同时对所有边二分,不妨考虑整体二分。
对于一个区间 \([l,r]\),记 \(G\) 表示所有最小出现时间在 \([l,r]\) 的边的集合。
每次把时间在 \([1,mid]\) 的边跑一个 Tarjan,如果两端是同一个 SCC 的,就递归进左边,否则递归进右边。
当然不能每次都把 \([1,mid]\) 的边加进去,可以考虑只加 \([l,mid]\) 的边,分治时右区间继承一下左区间加的边即可,这里具体可以看代码。
复杂度 \(O(q\log q)\)。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 5e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n, m, q;
struct dsu {
int fa[N], siz[N], n;
long long res;
void init( int _n) {
n = _n, res = 0;
for ( int i = 1; i <= n; i ++) fa[i] = i, siz[i] = 1;
}
int find( int x) {
return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
void merge( int x, int y) {
x = find(x), y = find(y);
if (x == y) return ;
if (siz[x] > 1) res -= 1ll * siz[x] * siz[x];
if (siz[y] > 1) res -= 1ll * siz[y] * siz[y];
fa[y] = x, siz[x] += siz[y], siz[y] = 0;
res += 1ll * siz[x] * siz[x];
}
} D;
vector< int> sta;
vector< int> G[N];
int vis[N], dfn[N], low[N], scc[N];
int tot;
int cnt;
void tarjan( int u) {
sta.push_back(u), vis[u] = 1;
dfn[u] = low[u] = ++ tot;
for ( auto v : G[u]) {
if (! dfn[v]) tarjan(v), low[u] = min(low[u], low[v]);
else if (vis[v]) low[u] = min(low[u], dfn[v]);
}
if (dfn[u] != low[u]) return ;
int v; cnt ++;
do {
v = sta.back(); sta.pop_back(), vis[v] = 0;
scc[v] = cnt;
} while (v != u) ;
}
vector< tuple< int, int, int> > e;
vector< int> vec[N];
void clear( int u) {
G[u].clear();
dfn[u] = low[u] = scc[u] = 0;
}
void solve( int l, int r, const vector< tuple< int, int, int> > & E) {
int mid = (l + r) >> 1;
cnt = tot = 0;
for ( auto [u, v, w] : E)
clear(u), clear(v);
for ( auto [u, v, w] : E)
if (w <= mid) G[u].push_back(v);
for ( auto [u, v, w] : E)
if (! dfn[u]) tarjan(u);
if (l == r) {
for ( auto [u, v, w] : E)
if (scc[u] == scc[v])
D.merge(get<0>(e[w - 1]), get<1>(e[w - 1]));
cout << D.res << '\n';
return ;
}
vector< tuple< int, int, int> > q1, q2;
for ( auto [u, v, w] : E) {
if (scc[u] == scc[v]) {
if (w <= mid) q1.push_back({u, v, w});
} else q2.push_back({scc[u], scc[v], w}); //这里直接用求出来的 scc 编号,就相当于继承了左区间跑的 Tarjan 信息。
}
solve(l, mid, q1), solve(mid + 1, r, q2);
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m >> q;
for ( int i = 1; i <= q; i ++) {
int u, v;
string op;
cin >> u >> v >> op;
if (op[0] == 'R') e.push_back({v + n, u, i});
else e.push_back({u, v + n, i});
}
D.init(n + m);
solve(1, q, e);
return 0;
}
[HNOI2010] 城市建设
考虑时间分治。
对于一个时间区间,把这个时间内要修改的边成为“动态边”,把不在这个时间内的边成为“静态边”。
那么关于最小生成树有一些结论:
- 如果把所有“动态边”的边权改成 \(\infin\) 跑 Kruskal,没有被选进去的“静态边”以后就不可能被选进去。
- 如果把所有“动态边”的边权改成 \(-\infin\) 跑 Kruskal,被选进去的“静态边”以后就一定会被选进去。
根据这个,不难想到维护一个集合 \(may\),表示可能被选进的边集。
对于永远不会被选进的边,就把它去掉;对于一定会选进去的边,把这条边合并成一个点,加上边权后去掉。这样每个区间的边数一定是 \(O(len)\) 的。
这种做法就是比较经典的时间分治。
具体实现看代码。
代码
#include <bits/stdc++.h>
#define int long long
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e4 + 10, M = 5e4 + 10, inf = 1e9, mod = 998244353;
int n, m, q;
int RES;
int ans[M];
struct edge {
int u, v, w;
} E[M], tE[M];
struct mdf {
int i, w;
} Q[M];
struct DSU {
int fa[N], siz[N], n;
vector< pair< int, int> > del;
set< int> S; // S 表示缩完点之后的点集
DSU() {}
DSU( int _n) {
n = _n; del.clear(), S.clear();
for ( int i = 1; i <= n; i ++) siz[i] = 1, fa[i] = i, S.insert(i);
}
int find( int x) {
return x == fa[x] ? x : find(fa[x]);
}
int find2( int x) {
return x == fa[x] ? x : fa[x] = find2(fa[x]);
}
int merge( int u, int v) {
u = find(u), v = find(v);
if (u == v) return 0;
if (siz[u] < siz[v]) swap(u, v);
del.push_back({u, v});
siz[u] += siz[v], fa[v] = u, S.erase(v);
return 1;
}
void Del() {
if (! del.size()) return ;
auto [u, v] = del.back(); del.pop_back();
siz[u] -= siz[v], fa[v] = v, S.insert(v);
}
} D1, D2;
// D1:维护缩点的可撤销并查集
// D2:求最小生成树时的普通并查集
set< int> get( set< int> s) {
vector< int> vec;
for ( auto i : D1.S) D2.fa[i] = i;
for ( auto i : s) vec.push_back(i);
sort(vec.begin(), vec.end(), [&]( int a, int b) {
return E[a].w < E[b].w;
});
set< int> res;
for ( auto i : vec) {
auto [u, v, w] = E[i];
u = D1.find(u), v = D1.find(v);
u = D2.find2(u), v = D2.find2(v);
if (u == v) continue ;
D2.fa[v] = u;
res.insert(i);
}
return res;
}
// 对边集 s 求出最小生成树的边集
set< int> may;
// 可能选进的边的集合
void solve( int l, int r) {
if (l == r) {
ans[l] = RES;
if (D1.siz[D1.find(1)] != n)
ans[l] += min(Q[l].w, (int)may.size() ? E[* may.begin()].w : inf);
// 判断图是否连通,若不连通,要么选自己这条边,要么选最后剩下的那条“静态边”
return ;
}
int mid = (l + r) >> 1;
set< int> L, R, tmay = may, supt;
int tRES = RES, tot = 0;
for ( int i = l; i <= mid; i ++) L.insert(Q[i].i);
for ( int i = mid + 1; i <= r; i ++) R.insert(Q[i].i);
for ( auto i : R) if (! L.count(i)) may.insert(i);
may = get(may);
supt = may;
for ( int i = l; i <= mid; i ++) E[Q[i].i].w = -inf, supt.insert(Q[i].i);
supt = get(supt);
for ( int i = l; i <= mid; i ++) E[Q[i].i].w = tE[Q[i].i].w;
for ( auto i : supt) if (may.count(i))
may.erase(i), tot += D1.merge(E[i].u, E[i].v), RES += E[i].w;
solve(l, mid);
while (tot) D1.Del(), tot --;
may = tmay, RES = tRES;
for ( int i = l; i <= mid; i ++) E[Q[i].i].w = tE[Q[i].i].w = Q[i].w;
// 将左区间的边修改后,处理右区间
for ( auto i : L) if (! R.count(i)) may.insert(i);
may = get(may);
supt = may;
for ( int i = mid + 1; i <= r; i ++) E[Q[i].i].w = -inf, supt.insert(Q[i].i);
supt = get(supt);
for ( int i = mid + 1; i <= r; i ++) E[Q[i].i].w = tE[Q[i].i].w;
for ( auto i : supt) if (may.count(i))
may.erase(i), tot += D1.merge(E[i].u, E[i].v), RES += E[i].w;
solve(mid + 1, r);
while (tot) D1.Del(), tot --;
may = tmay, RES = tRES;
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m >> q;
D1 = DSU(n);
for ( int i = 1; i <= m; i ++) {
int u, v, w;
cin >> u >> v >> w;
tE[i] = E[i] = {u, v, w}, may.insert(i);
}
for ( int i = 1; i <= q; i ++) {
int id, w; cin >> id >> w;
Q[i] = {id, w};
may.erase(id);
}
may = get(may);
set< int> supt = may;
for ( int i = 1; i <= q; i ++) E[Q[i].i].w = -inf, supt.insert(Q[i].i);
supt = get(supt);
for ( int i = 1; i <= q; i ++) E[Q[i].i].w = tE[Q[i].i].w;
for ( auto i : supt) if (may.count(i))
may.erase(i), D1.merge(E[i].u, E[i].v), RES += E[i].w;
// 先对全局跑一次
solve(1, q);
for ( int i = 1; i <= q; i ++) cout << ans[i] << '\n';
return 0;
}
「FeOI Round 4.5」はぐ
因为异或满足可减性,对于一条路径 \((u,v)\) 考虑树上差分变成四条链的询问,记 \(l\) 为 \({\rm lca}(u,v)\):
- \(\oplus_{x\in u\to 1}a_x-dep_x+dep_u\)
- \(\oplus_{x\in v\to 1}a_x+dep_x+dep_u-2dep_{l}\)
- \(\oplus_{x\in l\to 1}a_x-dep_x+dep_u\)
- \(\oplus_{x\in fa_l\to 1}a_x+dep_x+dep_u-2dep_{l}\)
\(a_x-dep_x+dep_u\) 与 \(a_x+dep_x+dep_u-2dep_l\) 显然是两种对称询问,这里以前者为例。
记 \(w_x\) 为 \(a_x-dep_x\)、\(dep_u\) 为 \(val\),询问就转化成把一条链上的数给加上一个常数,然后求异或和。
既然又有异或又有加减,考虑拆位。
对于第 \(k\) 位,记 \(op\) 表示 \(w_x+val\) 的第 \(k\) 位是否进位,那么对于 \(x\),第 \(k\) 位的值就是 \({\rm bit}_k(w_x)\oplus{\rm bit}_k(val)\oplus op\)。
考虑把这三个值分开维护。
对于 \(\oplus {\rm bit}_k(w_x)\),就是树上前缀异或和;对于 \(\oplus {\rm bit}_k(val)\),只需要考虑 \(dep_x\);对于 \(\oplus op\),首先 \(op=[w_x\bmod 2^k+val\bmod 2^k\ge 2^k]\),可以变形成 \(op=[w_x\bmod 2^k\ge 2^k-val\bmod 2^k]\),把 \(\ge\) 后面的看作常数,求这个就可以在 dfs 时同时用树状数组维护,具体是 \(x\) 刚进递归栈时,把它加入树状数组,出栈后就在树状数组中删除,查询就是一个后缀。
代码实现唯一注意的是可能有负数,这个用 unsigned int 处理即可。
代码
#include <bits/stdc++.h>
#define ui unsigned int
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n, q;
int a[N];
struct que {
ui val;
int id;
} ;
struct bit {
int tr[1 << 20];
void upd( int u) {
u ++;
for (; u; u -= (u & -u)) tr[u] ^= 1;
}
int ask( int u, int res = 0) {
u ++;
for (; u < (1 << 20); u += (u & -u)) res ^= tr[u];
return res;
}
} t;
vector< que> q1[N], q2[N];
ui w1[N], w2[N];
int ans[N];
int siz[N], dep[N], fa[N], son[N], top[N];
vector< int> G[N];
void dfs1( int u, int fu) {
fa[u] = fu, siz[u] = 1, dep[u] = dep[fu] + 1;
for ( auto v : G[u]) {
if (v == fu) continue ;
dfs1(v, u);
siz[u] += siz[v];
son[u] = (siz[v] > siz[son[u]] ? v : son[u]);
}
}
void dfs2( int u, int topt) {
top[u] = topt;
if (son[u]) dfs2(son[u], topt);
for ( auto v : G[u]) {
if (v == fa[u] || v == son[u]) continue ;
dfs2(v, v);
}
}
int lca( int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
u = fa[top[u]];
}
return (dep[u] < dep[v] ? u : v);
}
void dfs3( int u, int k, ui sx, int op) {
int mask = ((1 << k) - 1);
ui w = (op ? w1[u] : w2[u]);
sx ^= w;
t.upd(w & mask);
for ( auto [val, id] : (op ? q1[u] : q2[u])) {
ui res = t.ask((1 << k) - (val & mask));
ui bit = ((val >> k) & 1);
ans[id] ^= ((((sx >> k) & 1) ^ res ^ ((dep[u] & 1) ? bit : 0)) << k);
}
for ( auto v : G[u])
if (v != fa[u]) dfs3(v, k, sx, op);
t.upd(w & mask);
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> q;
for ( int i = 1; i <= n; i ++) cin >> a[i];
for ( int i = 1; i < n; i ++) {
int u, v; cin >> u >> v;
G[u].push_back(v), G[v].push_back(u);
}
dfs1(1, 0), dfs2(1, 1);
for ( int i = 1; i <= n; i ++) w1[i] = (ui)(a[i] - dep[i]), w2[i] = (ui)(a[i] + dep[i]);
for ( int i = 1; i <= q; i ++) {
int u, v; cin >> u >> v;
int l = lca(u, v);
q1[u].push_back({(ui)dep[u], i});
q2[v].push_back({(ui)(dep[u] - 2 * dep[l]), i});
q1[l].push_back({(ui)dep[u], i});
q2[fa[l]].push_back({(ui)(dep[u] - 2 * dep[l]), i});
}
for ( int i = 0; i < 20; i ++)
dfs3(1, i, 0, 1), dfs3(1, i, 0, 0);
for ( int i = 1; i <= q; i ++) cout << ans[i] << '\n';
return 0;
}
Big Wins!
对于最小值,很套路的把它的极长最小区间求出来,可以用单调栈。
对于一个最小值为 \(x\) 的区间 \([l,r]\),如何求出里面最大的中位数?
考虑去二分这个中位数 \(y\),很经典的结论,若把 \(\lt y\) 的数看作 \(-1\),把 \(\ge y\) 的数看作 \(1\),那如果存在 \(\ge y\) 的中位数,要满足它们的和 \(\ge 0\)。
所以为了尽可能满足能够选出 \(y\),肯定想要和最大。
那么相当于在 \([l,i-1]\) 选出一个最大后缀和、\([i+1,r]\) 选出一个最大前缀和即可。
最大后缀和与最大前缀和可以用线段树维护出来,但是因为要二分中位数 \(y\),需要得到所有 \(y\) 对应的 \(-1\)、\(1\) 序列,这里可以用主席树处理。
复杂度 \(O(n\log^2n)\)。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 5e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n, tot;
int a[N], rt[N];
struct sgt {
int sum, lmax, rmax;
} T[N * 20];
int ls[N * 20], rs[N * 20];
sgt merge( sgt a, sgt b) {
return {a.sum + b.sum, max(a.lmax, a.sum + b.lmax), max(b.rmax, b.sum + a.rmax)};
}
void ins( int lk, int & k, int l, int r, int x, int v) {
k = ++ tot;
T[k] = T[lk], ls[k] = ls[lk], rs[k] = rs[lk];
if (l == r) {
T[k] = {v, max(0, v), max(0, v)};
return ;
}
int mid = (l + r) >> 1;
x <= mid ? ins(ls[lk], ls[k], l, mid, x, v) : ins(rs[lk], rs[k], mid + 1, r, x, v);
T[k] = merge(T[ls[k]], T[rs[k]]);
}
sgt ask( int k, int l, int r, int x, int y) {
if (x > y || ! k) return {0, 0, 0};
if (x <= l && r <= y) return T[k];
int mid = (l + r) >> 1;
if (y <= mid) return ask(ls[k], l, mid, x, y);
if (x > mid) return ask(rs[k], mid + 1, r, x, y);
return merge(ask(ls[k], l, mid, x, y), ask(rs[k], mid + 1, r, x, y));
}
vector< int> vec[N];
int sta[N], top;
int L[N], R[N];
void solve() {
cin >> n;
for ( int i = 0; i <= n; i ++) rt[i] = 0, vec[i].clear();
for ( int i = 1; i <= n; i ++) cin >> a[i], vec[a[i]].push_back(i);
a[n + 1] = 0;
for ( int i = 0; i <= tot; i ++)
T[i] = {0, 0, 0}, ls[i] = rs[i] = 0;
tot = 0;
for ( int i = 1; i <= n; i ++) {
int root = rt[0];
ins(root, rt[0], 1, n, i, 1);
}
for ( int i = 1; i <= n; i ++) {
rt[i] = rt[i - 1];
for ( auto v : vec[i - 1]) {
int root = rt[i];
ins(root, rt[i], 1, n, v, -1);
}
}
top = 0;
for ( int i = 1; i <= n + 1; i ++) {
while (top && a[sta[top]] > a[i]) R[sta[top]] = i - 1, top --;
sta[++ top] = i;
}
top = 0;
for ( int i = n; i >= 0; i --) {
while (top && a[sta[top]] > a[i]) L[sta[top]] = i + 1, top --;
sta[++ top] = i;
}
int ans = 0;
for ( int i = 1; i <= n; i ++) {
int l = 1, r = n;
while (l < r) {
int mid = (l + r + 1) >> 1;
if (ask(rt[mid], 1, n, L[i], i - 1).rmax + (a[i] < mid ? -1 : 1) + ask(rt[mid], 1, n, i + 1, R[i]).lmax >= 0) l = mid;
else r = mid - 1;
}
ans = max(ans, l - a[i]);
}
cout << ans << '\n';
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T; cin >> T;
while (T --) solve();
return 0;
}
Farmer John's Favorite Function
首先发现若每次只保留 \(f(i)\) 的整数部分,答案是不变的,所以只用考虑每次对 \(f(i)\) 向下取整的结果。
可以想到一个做法,对时间开一颗线段树,然后从 \(1\sim n\) 枚举 \(a_i\),给对应位置加上对应的 \(a_i\)(\(a_i\) 的相邻两次修改内值是一样的,那么就是一个区间加)。
然后每次给所有位置开根号即可。
考虑势能线段树,发现一个数开几次根号就会趋近于 \(1\)。
那么线段树上维护一个最大值 \(mx\) 与最小值 \(mi\),若线段树上一个区间满足 \(mx-\lfloor\sqrt mx\rfloor=mi -\lfloor \sqrt mi\rfloor\),那么这整段区间都相当于减去了 \(\lfloor\sqrt mx\rfloor-mx\),打一个加的标记即可,对于其他的位置就递归到叶子即可。
复杂度 \(O(m\log m\log V)\)。
代码
#include <bits/stdc++.h>
#define int long long
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n, m;
int a[N];
int mysqrt( int x) {
int res = sqrtl(x);
while (res * res > x) res -= 1;
while ((res + 1) * (res + 1) <= x) res += 1;
return res;
}
struct sgt {
#define ls k << 1
#define rs k << 1 | 1
#define mid ((l + r) >> 1)
#define lson ls, l, mid
#define rson rs, mid + 1, r
int mx[N * 4], mi[N * 4], tag[N * 4];
void psu( int k) {
mx[k] = max(mx[ls], mx[rs]);
mi[k] = min(mi[ls], mi[rs]);
}
void pst( int k, int v) {
mx[k] += v, mi[k] += v, tag[k] += v;
}
void psd( int k) {
if (! tag[k]) return ;
pst(ls, tag[k]), pst(rs, tag[k]);
tag[k] = 0;
}
void upd( int x, int y, int v, int k = 1, int l = 1, int r = m) {
if (x > y) return ;
if (x <= l && r <= y) return pst(k, v);
psd(k);
if (x <= mid) upd(x, y, v, lson);
if (y > mid) upd(x, y, v, rson);
psu(k);
}
void sQrt( int x, int y, int k = 1, int l = 1, int r = m) {
if (x > y) return ;
if (l == r) return mx[k] = mysqrt(mx[k]), mi[k] = mysqrt(mi[k]), void();
if (x <= l && r <= y && mx[k] - mysqrt(mx[k]) == mi[k] - mysqrt(mi[k])) return pst(k, mysqrt(mx[k]) - mx[k]);
psd(k);
if (x <= mid) sQrt(x, y, lson);
if (y > mid) sQrt(x, y, rson);
psu(k);
}
void print( int k = 1, int l = 1, int r = m) {
if (l == r) return cout << mi[k] << '\n', void();
psd(k);
print(lson), print(rson);
}
#undef ls
#undef rs
#undef mid
#undef lson
#undef rson
} T;
vector< pair< int, int> > que[N];
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for ( int i = 1; i <= n; i ++) cin >> a[i];
for ( int i = 1; i <= m; i ++) {
int p, x; cin >> p >> x;
que[p].push_back({x, i});
}
for ( int i = 1; i <= n; i ++) {
int lstt = 1, lstv = a[i];
for ( auto [val, tim] : que[i]) {
T.upd(lstt, tim - 1, lstv);
lstt = tim, lstv = val;
}
T.upd(lstt, m, lstv);
T.sQrt(1, m);
}
T.print();
return 0;
}
树锯解构
没有原题。
给一个序列,区间加对 \(2^m\) 取模,询问区间与。
\(n,q\le 5\times 10^5,m\le32\)。
考虑拆位,对 \(a_i\) 考虑它的第 \(k\) 位是 \(1\) 的情况,发现可以求出一个 \([l,r]\),满足 \([a_i+l\bmod 2^k,a_i+r\bmod 2^k)\) 在 \([2^k,2^{k+1})\) 中,也就是说给 \(a_i\) 加上 \([l,r]\) 中的一个数,可以使得 \(a_i\) 的第 \(k\) 位是 \(1\)。
那么每次区间加操作都是把 \(l\) 和 \(r\) 减去一个数,其实就是把 \(l\) 和 \(r\) 看作在一个长度为 \(2^{k+1}\) 的环上移动。
询问时若第 \(k\) 位的区间与是 \(1\),那么就要满足所有的 \([l,r]\) 交集有 \(0\)。
放在线段树上维护 \(l,r\) 的交集情况即可。
代码
#include <bits/stdc++.h>
#define int long long
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 5e5 + 10, M = 2e5 + 10, inf = 1e9;
int n, q, m;
int a[N];
int mod[32];
struct sgt {
#define ls k << 1
#define rs k << 1 | 1
#define mid ((l + r) >> 1)
struct node {
int l[32], r[32];
node() {
memset(l, -1, sizeof l);
memset(r, -1, sizeof r);
}
} tr[N * 4];
int tag[N * 4];
node merge( node a, node b) {
node res = node();
for ( int i = 0; i < m; i ++) {
int l1 = a.l[i], r1 = a.r[i], l2 = b.l[i], r2 = b.r[i];
if (l1 == -1 || l2 == -1) continue ;
if (l1 > r1) {
if (l2 > r2) res.l[i] = max(l1, l2), res.r[i] = min(r1, r2);
else if (l2 <= r1) res.l[i] = l2, res.r[i] = min(r1, r2);
else if (r2 >= l1) res.r[i] = r2, res.l[i] = max(l1, l2);
} else {
if (l2 <= r2) {
res.l[i] = max(l1, l2), res.r[i] = min(r1, r2);
if (res.l[i] > res.r[i]) res.l[i] = res.r[i] = -1;
} else {
swap(l1, l2), swap(r1, r2);
if (l2 <= r1) res.l[i] = l2, res.r[i] = min(r1, r2);
else if (r2 >= l1) res.r[i] = r2, res.l[i] = max(l1, l2);
}
}
}
return res;
}
void pst( int k, int v) {
for ( int i = 0; i < m; i ++) {
if (tr[k].l[i] == -1) continue ;
tr[k].l[i] = (tr[k].l[i] - (v & (mod[i] - 1)) + mod[i]) & (mod[i] - 1);
tr[k].r[i] = (tr[k].r[i] - (v & (mod[i] - 1)) + mod[i]) & (mod[i] - 1);
}
tag[k] += v;
}
void psd( int k) {
if (! tag[k]) return ;
pst(ls, tag[k]), pst(rs, tag[k]);
tag[k] = 0;
}
void build( int k = 1, int l = 1, int r = n) {
tr[k] = node(), tag[k] = 0;
if (l == r) {
for ( int i = 0; i < m; i ++) {
int x = a[l] & (mod[i] - 1);
tr[k].l[i] = ((mod[i] >> 1) - x + mod[i]) & (mod[i] - 1);
tr[k].r[i] = (tr[k].l[i] + (mod[i] >> 1) - 1) & (mod[i] - 1);
}
return ;
}
build(ls, l, mid), build(rs, mid + 1, r);
tr[k] = merge(tr[ls], tr[rs]);
}
void upd( int x, int y, int v, int k = 1, int l = 1, int r = n) {
if (x <= l && r <= y) return pst(k, v);
psd(k);
if (x <= mid) upd(x, y, v, ls, l, mid);
if (y > mid) upd(x, y, v, rs, mid + 1, r);
tr[k] = merge(tr[ls], tr[rs]);
}
node ask( int x, int y, int k = 1, int l = 1, int r = n) {
if (x <= l && r <= y) return tr[k];
psd(k);
if (y <= mid) return ask(x, y, ls, l, mid);
if (x > mid) return ask(x, y, rs, mid + 1, r);
return merge(ask(x, y, ls, l, mid), ask(x, y, rs, mid + 1, r));
}
} T;
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> q >> m;
for ( int i = 0; i < m; i ++) mod[i] = (1ll << (i + 1));
for ( int i = 1; i <= n; i ++) cin >> a[i];
T.build();
while (q --) {
int op, l, r, x;
cin >> op >> l >> r;
l ++;
if (! op) {
cin >> x;
T.upd(l, r, x);
} else {
auto res = T.ask(l, r);
int ans = 0;
for ( int i = 0; i < m; i ++) if (res.l[i] != -1 && (res.l[i] > res.r[i] || res.l[i] == 0)) ans |= (1ll << i);
cout << ans << '\n';
}
}
return 0;
}
Building Forest Trails
先把环断开,如果两个区间有交集,那么就代表这两个区间构成一个连通块。
对于一个连通块,内部的连边是不重要的,可以只连接有用的边。(这个连通块构成的凸多边形上的边)
那么对于不同的连通块,它们之间的边是不交的,只有包含关系。
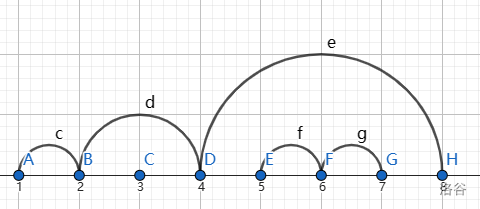
就比如这个图,\(1\)、\(2\)、\(4\)、\(8\) 是一个连通块,\(3\) 是一个连通块,\(5\)、\(6\)、\(7\) 是一个连通块。
然后考虑去维护这个包含的关系,记 \(h_x\) 为 \(x\) 上面的弧的个数(端点不算)。
考虑给 \(x\) 与 \(y\) 加边,默认 \(x\lt y\),这里分两种情况。
- \(h_x\gt h_y\),那么考虑找到 \(x\) 右边第一个 \(p\) 满足 \(h_p\lt h_x\),显然这个 \(p\lt y\) ,那么把 \(x\) 和 \(p\) 的连通块合并。
- \(h_x\lt h_y\),那么考虑找到 \(y\) 左边第一个 \(p\),满足 \(h_p\lt h_y\),然后把 \(p\) 和 \(y\) 连通块合并。
- \(h_x=h_y\),考虑找到 \(x\) 右边第一个 \(p\),若 \(p\ge y\) 说明连接了 \(x\)、\(y\) 不与其他连通块产生交集,可以直接合并,否则就合并 \(x\) 与 \(p\) 的连通块。
一只做,直到 \(x\) 与 \(y\) 在同一个连通块,合并的总次数是 \(O(n)\) 的。
考虑如何合并?
若合并的两个连通块没有包含关系,那么直接连接第一个连通块的右端点和第二个连通块的左端点即可,也就是把 \((R_1,L_2)\) 的 \(h\) 给加一。
如果合并的两个连通块有包含关系,那么会删掉大连通块包含小连通块的那条边,然后加上小连通块与大连通块的左、右端点相连的两条边,也就是把 \([\max (L_1, L_2),\min(R_1,R_2)]\) 的 \(h\) 减一。
所以维护一颗 \(h\) 的线段树即可,找 \(p\) 可以用线段树二分。
复杂度 \(O(n\log n)\)。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n, m;
struct DSU {
int fa[N], L[N], R[N];
void init() {
for ( int i = 1; i <= n; i ++) fa[i] = L[i] = R[i] = i;
}
int find( int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void merge( int u, int v) {
u = find(u), v = find(v);
if (u == v) return ;
fa[v] = u, L[u] = min(L[u], L[v]), R[u] = max(R[u], R[v]);
}
} D;
struct sgt {
#define ls k << 1
#define rs k << 1 | 1
#define mid ((l + r) >> 1)
#define lson ls, l, mid
#define rson rs, mid + 1, r
int mi[N * 4], tag[N * 4];
void psu( int k) {
mi[k] = min(mi[ls], mi[rs]);
}
void pst( int k, int v) {
mi[k] += v, tag[k] += v;
}
void psd( int k) {
if (! tag[k]) return ;
pst(ls, tag[k]), pst(rs, tag[k]);
tag[k] = 0;
}
void upd( int x, int y, int v, int k = 1, int l = 1, int r = n) {
if (x > y) return ;
if (x <= l && r <= y) return pst(k, v);
psd(k);
if (x <= mid) upd(x, y, v, lson);
if (y > mid) upd(x, y, v, rson);
psu(k);
}
int ask( int x, int k = 1, int l = 1, int r = n) {
if (l == r) return mi[k];
psd(k);
return x <= mid ? ask(x, lson) : ask(x, rson);
}
int findl( int x, int v, int k = 1, int l = 1, int r = n) {
if (r <= x) {
if (mi[k] >= v) return 0;
if (l == r) return l;
psd(k);
if (mi[rs] < v) return findl(x, v, rson);
return findl(x, v, lson);
}
int res = 0;
psd(k);
if (x > mid) res = findl(x, v, rson);
if (res == 0) res = findl(x, v, lson);
return res;
}
int findr( int x, int v, int k = 1, int l = 1, int r = n) {
if (l >= x) {
if (mi[k] >= v) return n + 1;
if (l == r) return l;
psd(k);
if (mi[ls] < v) return findr(x, v, lson);
return findr(x, v, rson);
}
int res = n + 1;
psd(k);
if (x <= mid) res = findr(x, v, lson);
if (res == n + 1) res = findr(x, v, rson);
return res;
}
#undef ls
#undef rs
#undef mid
#undef lson
#undef rson
} T;
void merge( int u, int v) {
u = D.find(u), v = D.find(v);
if (D.R[u] < D.L[v]) T.upd(D.R[u] + 1, D.L[v] - 1, 1);
else T.upd(max(D.L[u], D.L[v]), min(D.R[u], D.R[v]), -1);
D.merge(u, v);
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
D.init();
while (m --) {
int op, x, y;
cin >> op >> x >> y;
if (op == 1) {
if (x > y) swap(x, y);
while (D.find(x) != D.find(y)) {
int vx = T.ask(x), vy = T.ask(y);
if (vx == vy) {
int p = T.findr(x, vx);
if (p < y) merge(x, p);
else merge(x, y);
} else if (vx > vy) merge(x, T.findr(x, vx));
else merge(y, T.findl(y, vy));
}
} else cout << (D.find(x) == D.find(y));
}
return 0;
}
点心
没有原题。
给一个 \(n\times m\) 的矩阵。
定义一个子矩阵的价值是其中的元素和的平方,但如果子矩阵中出现了 \(-1\),那么价值为 \(0\)。
求所有子矩阵的价值和。
\(n,m\le 2500,-1\le a_{i,j}\le 998244353\)。
对于一个子矩阵,它的贡献可以看作 \((A-B-C+D)^2\),把它拆开有:
发现本质不同的只有三种类型:
- 平方,例如 \(AA\)。
- 矩形平行项乘积,例如 \(AB\)。
- 矩形对角线乘积,例如 \(AD\)。
考虑对这些东西分开计算。
枚举一个矩形的下边界,然后对每一列求出上方第一个 \(-1\),记 \(h_j\) 表示第 \(j\) 列从下边界到 \(-1\) 的距离。
对 \(h_j\) 建立笛卡尔树,对于一个 \(h_j\) 为最小值的区间 \([L,R]\),所有跨过 \(j\) 的子矩阵都是合法的,统计即可。
统计需要用到二维前缀和,二维前缀和的二维前缀和,二维前缀和的平方的二维前缀和。具体看代码。
代码
#include <bits/stdc++.h>
// #define long long
void Freopen() {
freopen("rena.in", "r", stdin);
freopen("rena.out", "w", stdout);
}
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n, m;
int a[2501][2501];
int s[2501][2501], sum[2501][2501], spw[2501][2501];
int add( int x, int v) {
x += v;
return x >= mod ? x - mod : x;
}
int ask( int a, int b, int c, int d, int S[][2501]) {
a = max(0, a - 1), b = max(0, b - 1);
return (0ll + S[c][d] - S[a][d] + mod - S[c][b] + mod + S[a][b]) % mod;
}
int h[N];
int ls[N], rs[N], sta[N], top;
int A, B, C;
// A:平方项的和 B:平行项乘积和 C:对角线乘积和
void build( int n) {
for ( int i = 1; i <= n; i ++) ls[i] = rs[i] = 0;
top = 0;
for ( int i = 1; i <= n; i ++) {
int k = top;
while (top && h[sta[top]] > h[i]) top --;
if (k != top) ls[i] = sta[top + 1];
if (top) rs[sta[top]] = i;
sta[++ top] = i;
}
}
void cal1( int u, int l, int r, int i, int op) {
if (ls[u]) cal1(ls[u], l, u - 1, i, op);
if (rs[u]) cal1(rs[u], u + 1, r, i, op);
if (! h[u]) return ;
A = add(A, 1ll * h[u] * (u - l + 1) % mod * ask(i, u, i, r, spw) % mod);
A = add(A, 1ll * h[u] * (r - u + 1) % mod * ask(i, l - 1, i, u - 1, spw) % mod);
B = add(B, 1ll * h[u] * ask(i, l - 1, i, u - 1, sum) % mod * ask(i, u, i, r, sum) % mod);
if (op) return ;
C = add(C, 1ll * ask(i, u, i, r, sum) * ask(i - h[u], l - 1, i - 1, u - 1, sum) % mod);
C = add(C, 1ll * ask(i, l - 1, i, u - 1, sum) * ask(i - h[u], u, i - 1, r, sum) % mod);
}
void cal2( int u, int l, int r, int i) {
if (ls[u]) cal2(ls[u], l, u - 1, i);
if (rs[u]) cal2(rs[u], u + 1, r, i);
if (! h[u]) return ;
B = add(B, 1ll * h[u] * ask(l - 1, i, u - 1, i, sum) % mod * ask(u, i, r, i, sum) % mod);
}
signed main() {
Freopen();
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for ( int i = 1; i <= n; i ++)
for ( int j = 1; j <= m; j ++)
cin >> a[i][j];
for ( int i = 1; i <= n; i ++)
for ( int j = 1; j <= m; j ++) {
s[i][j] = (0ll + (a[i][j] == -1 ? 0 : a[i][j]) + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mod) % mod;
sum[i][j] = (0ll + s[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mod) % mod;
spw[i][j] = (0ll + 1ll * s[i][j] * s[i][j] % mod + spw[i - 1][j] + spw[i][j - 1] - spw[i - 1][j - 1] + mod) % mod;
}
for ( int i = 1; i <= m; i ++ ) h[i] = 0;
for ( int i = 1; i <= n; i ++) {
for ( int j = 1; j <= m; j ++) h[j] = (a[i][j] == -1 ? 0 : h[j] + 1);
build(m);
cal1(sta[1], 1, m, i, 0);
}
for ( int i = 1; i <= m; i ++) h[i] = 0;
for ( int i = n; i; i --) {
for ( int j = 1; j <= m; j ++) h[j] = (a[i][j] == -1 ? 0 : h[j] + 1);
build(m);
cal1(sta[1], 1, m, i - 1, 1);
}
for ( int i = 1; i <= n; i ++) h[i] = 0;
for ( int j = 1; j <= m; j ++) {
for ( int i = 1; i <= n; i ++) h[i] = (a[i][j] == -1 ? 0 : h[i] + 1);
build(n);
cal2(sta[1], 1, n, j);
}
for ( int i = 1; i <= n; i ++) h[i] = 0;
for ( int j = m; j; j --) {
for ( int i = 1; i <= n; i ++) h[i] = (a[i][j] == -1 ? 0 : h[i] + 1);
build(n);
cal2(sta[1], 1, n, j - 1);
}
cout << ((0ll + A - B - B + C + C) % mod + mod) % mod << '\n';
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号