数数
Trick
-
对于限制特殊的序列计数，可以转化成一种具体的形态再计数。（[ZJOI2010] 排列计数）
-
计算无标号的方案数，可以转化成带标号的方案数。（[HNOI2011] 卡农）
-
对于排列变换题，考虑转化、转化、再转化！直到好求。（随机左移）
-
计算排列方案数时，设计的 dp 可以记排列的相对大小。（Permutation Blackhole）
-
有根 DAG 的生成树个数是除根外的所有点的入度的乘积，相当于给除根外的每个点定一个父亲。（[HNOI2015] 落忆枫音）
-
给无向图定向可以减少枚举复杂度。（无向图三元环计数）
-
关于值域的容斥，可以考虑按照值域从小到大排序。（CF2146F Bubble Sort）
-
给无向图定方向，然后统计一个点与集合 \(S\) 中的所有点连通的方案数，考虑枚举子集进行容斥。（赢家）
-
对于贡献为特殊值（例如：最大值、最小值）的计数，考虑去计算某个位置取到特殊值时的方案数。（[BalticOI 2024] Wall）
-
排列的置换，考虑把环建出来。（排列幂）
题目
[ZJOI2010] 排列计数
发现这个限制就是一个小根堆。
那么其实也就是在一个堆上填 \(1\sim n\) 的数字，使得这个堆成为一个小根堆。
设 \(f_i\) 表示有多少种填的方案使得第 \(i\) 个节点对应的堆为小根堆。
那么转移就是 \(f_i={{siz_i-1}\choose{siz_{2i}}} \times f_{2i}\times f_{2i+1}\)。
也就是在 \(siz_i-1\) 个数字中选择 \(siz_{2i}\) 个放进左子树，剩下 \(siz_i-1-siz_{2i}\) 个数放进右子树，使得左右子树都为小根堆的方案数。可以发现数字的具体值不用关心，因为只用在意它们的相对大小。
需要注意的是 \(n\) 可能大于 \(p\) 所以要用卢卡斯定理求组合数。
代码
#include <bits/stdc++.h>
#define int long long
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e6 + 10, M = 2e5 + 10, inf = 1e9;
int n, mod;
int f[N], siz[N];
int fac[N], inv[N];
void init( int n) {
fac[0] = inv[0] = inv[1] = 1;
for ( int i = 1; i <= n; i ++) fac[i] = fac[i - 1] * i % mod;
for ( int i = 2; i <= n; i ++) inv[i] = (mod - mod / i) * inv[mod % i] % mod;
for ( int i = 1; i <= n; i ++) inv[i] = inv[i - 1] * inv[i] % mod;
}
int C( int n, int m) {
if (n < m) return 0;
return fac[n] * inv[m] % mod * inv[n - m] % mod;
}
int Lucas( int n, int m) {
if (m == 0) return 1;
return (C(n % mod, m % mod) * Lucas(n / mod, m / mod)) % mod;
}
signed main() {
ios ::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> mod;
init(n);
for ( int i = 1; i <= n; i ++) siz[i] = 1;
for ( int i = n; i; i --) siz[i] += siz[i << 1] + siz[i << 1 | 1];
for ( int i = n + 1; i <= 2 * n + 1; i ++) f[i] = 1;
for ( int i = n; i; i --)
f[i] = Lucas(siz[i] - 1, siz[i << 1]) * f[i << 1] % mod * f[i << 1 | 1] % mod;
cout << f[1] << '\n';
return 0;
}
[HNOI2011] 卡农
首先可以转化题意，如果把每一种集合看成一个二进制，那么就是在 \(1\sim 2^n\) 的数中，选出 \(m\) 个互不相同的数，且这些数异或和为 \(0\) 的方案数。
考虑 dp，设 \(f_i\) 表示选了 \(i\) 个数且合法的方案数。为了方便计算，这个 dp 是带标号的，最后除一个 \(m!\) 即可。
考虑计算 \(f_i\)，首先，为了满足异或和为 \(0\) 的限制，可以发现如果确定了前面 \(i-1\) 个数，那么第 \(i\) 个数的选择方案是唯一确定的。
所以就有 \({\rm{A}}_{2^n-1}^{i-1}\) 种方案数，也就是前面 \(i-1\) 个数的方案数。
这样肯定是会算重的，在这 \({\rm{A}}_{2^n-1}^{i-1}\) 种方案数中，会有异或和为 \(0\) 的情况，这样就会导致第 \(i\) 个数为 \(0\)。
所以要减去前 \(i-1\) 个数的异或和为 \(0\) 的情况，也就是 \(f_{i-1}\)。
然后考虑去掉前 \(i-1\) 个数中，有与 \(i\) 相同的数的方案数。
这边钦定与 \(i\) 相同的数是 \(j\)，那么同时去掉 \(i\)、\(j\)，剩下的数也可以满足异或和为 \(0\)，其实也就是 \(f_{i-2}\)。
然后 \(i\) 与 \(j\) 要相同，有 \(2^n-1-(i-2)\) 种方案（减 \(i-2\) 是为了满足和剩下 \(i-2\) 个数不相同）；又因为 \(j\) 有 \(i-1\) 种选择，所以还要乘上 \(i-1\)。
最后就是要减去 \(f_{i-2}\times(2^n-i+1)\times(i-1)\)。
那么 \(f_i\) 就等于 \({\rm{A}}_{2^n-1}^{i-1} - f_{i-1} - f_{i-2}\times(2^n-i+1)\times(i-1)\)。
代码
#include <bits/stdc++.h>
#define int long long
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 1e6 + 10, M = 2e5 + 10, inf = 1e9, mod = 1e8 + 7;
int n, m, fac = 1;
int f[N];
int ksm( int a, int b, int res = 1) {
while (b) {
if (b & 1) res = res * a % mod;
a = a * a % mod, b >>= 1;
}
return res;
}
int A[N];
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
int pw = 1;
for ( int i = 1; i <= n; i ++) pw = pw * 2 % mod;
A[0] = 1;
for ( int i = 1; i <= m; i ++)
A[i] = A[i - 1] * (pw - i + mod) % mod,
fac = fac * i % mod;
f[0] = 1, f[1] = 0;
for ( int i = 2; i <= m; i ++) {
f[i] = A[i - 1];
f[i] = (f[i] - f[i - 1] + mod) % mod;
f[i] = (f[i] - f[i - 2] * (pw - i + 1 + mod) % mod * (i - 1) % mod + mod) % mod;
}
cout << f[m] * ksm(fac, mod - 2) % mod << '\n';
return 0;
}
随机左移
没有原题。
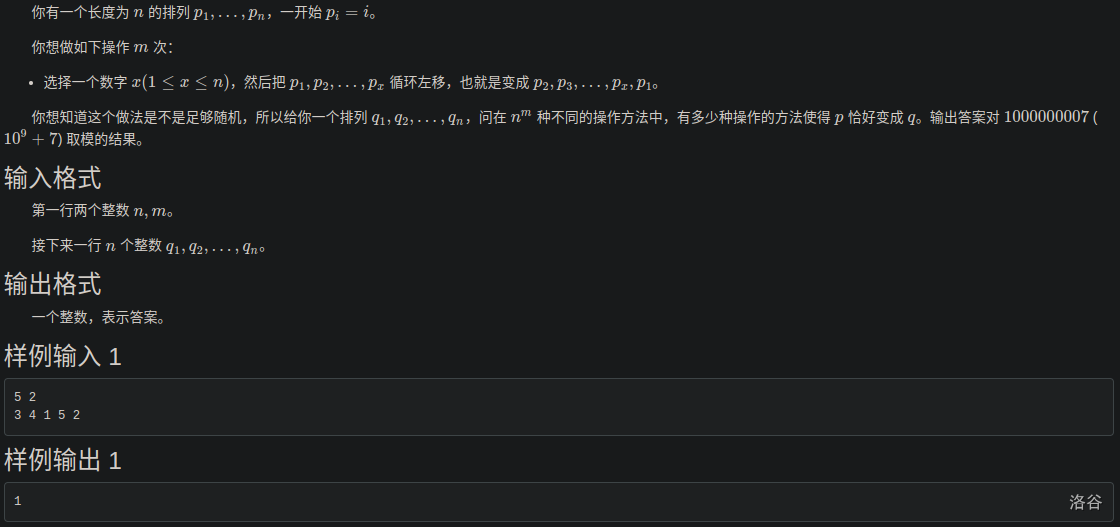
\(n,m\le 10^6\)，正解要用第二类斯特林数，这里就讨论 \(n,m\le 5000\) 的做法。
考虑如何从 \(q\) 变成 \(p\)，也就是到着做。
每次操作，也就是将一个数拿到最前面来。
不难发现的是，\(m\) 基本上是跑不满的，所以会有很多次重复操作来水满次数。
那么可以考虑先找到一个最小操作次数使得 \(q\) 为 \(p\)。
这个很简单，初始 \(x=n\)，先找到 \(q_i=x\)，然后再在 \([1,i)\) 中找 \(x-1\)，如果找到了，就让 \(x\leftarrow x-1\)；否则，就需要一次操作把 \(x-1\) 拿到最前面去，然后令 \(x\leftarrow x-1\)。
就例如 3 4 1 5 2，对于 \(3\sim 5\)，都是不用操作的，只需要操作 \(1\) 和 \(2\) 即可，最小操作次数就是 \(2\)。
于是就可以确定那些数能被操作，也就是说对于 3 4 1 5 2，\(1\)、\(2\) 是必须被操作的，\(3\sim 5\) 可操作也可以不操作。
再转化就变成了求钦定 \(1\sim 2\) 必须操作时、\(1\sim3\) 必须操作时、\(1\sim 4\) 必须操作时、\(1\sim 5\) 必须操作时的方案数的和。
那么就考虑怎么求 \(1\sim up\) 必须操作的方案数。
考虑对操作序列进行分析，记最后一次操作 \(x\) 时为第 \(i\) 次操作，那么在第 \((i,m]\) 次操作中，不可能操作比 \(x\) 大的数。
所以就可以考虑 dp，设 \(f_{i,j}\) 表示当前是第 \(i\) 次操作，当前是 \(j\) 最后一次出现的方案数。
这里考虑倒着转移，对于 \(f_{i,j}\) 从 \(f_{k,j-1}(k\gt i)\) 转移，也就是 \(f_{i,j}\leftarrow f_{k,j-1}\times {j-1}^{k-i-1}\)。
初始条件就是 \(f_{m,1}=1\)。
直接转移是 \(O(n^3)\) 的，可以后缀和优化到 \(O(n^2)\)。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 5e3 + 10, M = 2e5 + 10, inf = 1e9, mod = 1e9 + 7;
int n, m;
int q[N], rev[N];
int f[N][N], g[N][N];
int pw[N][N], inv[N][N];
int ksm( int a, int b, int res = 1) {
while (b) {
if (b & 1) res = 1ll * res * a % mod;
a = 1ll * a * a % mod, b >>= 1;
}
return res;
}
int add( int x, int v) {
x += v;
return x >= mod ? x - mod : x;
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for ( int i = 1; i <= n; i ++) cin >> q[i], rev[q[i]] = i;
for ( int i = 1; i <= n; i ++) {
pw[i][0] = 1, inv[i][0] = 1;
int Inv = ksm(i, mod - 2);
for ( int j = 1; j <= m; j ++)
pw[i][j] = 1ll * pw[i][j - 1] * i % mod,
inv[i][j] = 1ll * inv[i][j - 1] * Inv % mod;
}
int x = n;
while (x - 1 >= 1 && rev[x - 1] < rev[x]) x = x - 1;
f[m][1] = 1, g[m][1] = 1;
for ( int i = m - 1; i; i --) {
for ( int j = 1; j <= n; j ++)
f[i][j] = 1ll * g[i + 1][j - 1] * inv[j - 1][i] % mod,
g[i][j] = add(g[i + 1][j], 1ll * f[i][j] * pw[j][i - 1] % mod);
}
int ans = 0;
for ( int i = x - 1; i <= n; i ++)
for ( int j = 1; j <= m; j ++)
ans = add(ans, 1ll * f[j][i] * pw[i][j - 1] % mod);
cout << ans << '\n';
return 0;
}
Permutation Blackhole
这里要算排列，求排列是麻烦的，所以考虑求相对大小即可。
首先如果一个位置为染色，那么由它分割出来的两个区间相互就不能贡献，所以考虑区间 dp。
\(f_{l,r}\) 表示 \([l,r]\) 中的位置都没被染色过的方案数，考虑 \([l,r]\) 中最先被染色的位置 \(k\)，它会给 \(l-1\) 与 \(r+1\) 其中之一贡献分数，那么记 \(f_{l,r,x,y}\) 表示 \([l,r]\) 的位置全被染色，且给 \(l-1\) 贡献了 \(x\) 分数，\(r+1\) 贡献了 \(y\) 分数。
现在枚举分割点 \(k\)，记 \(w\) 为贡献分数的地方。
那么转移有：
这里乘 \(\binom{r-l}{k-l}\) 是因为只考虑排列的相对大小，所以在 \(r-l\) 个数中任意选 \(k-l\) 个给左区间，剩下的给右区间。
由于 \(s_k\) 有限制，所以当 \(s_k\neq -1\) 时，要满足 \(y+x'=s_k\)。
这里时间复杂度是 \(O(n^6)\) 的，考虑优化状态。
发现 \(x\)、\(y\) 的大小不会超过 \(\log n\)，原因是当一个位置给它贡献后，剩下的位置中能贡献的数量是原来的一半。
那么优化到 \(O(n^3\log^3 n)\)。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 110, M = 8, inf = 1e9, mod = 998244353;
int n;
int s[N], fac[N], inv[N];
int f[N][N][M][M];
int w( int l, int r, int k) {
if (r == n) return l - 1;
else if (l == 1) return r + 1;
else if (2 * k <= l + r) return l - 1;
return r + 1;
}
int add( int x, int v) {
x += v;
return x >= mod ? x - mod : x;
}
void init( int n) {
fac[0] = inv[0] = inv[1] = 1;
for ( int i = 1; i <= n; i ++) fac[i] = 1ll * fac[i - 1] * i % mod;
for ( int i = 2; i <= n; i ++) inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;
for ( int i = 1; i <= n; i ++) inv[i] = 1ll * inv[i - 1] * inv[i] % mod;
}
int C( int n, int m) {
if (n < m) return 0;
if (n == m) return 1;
return 1ll * fac[n] * inv[m] % mod * inv[n - m] % mod;
}
void solve() {
memset(f, 0, sizeof f);
cin >> n;
for ( int i = 1; i <= n; i ++) cin >> s[i];
init(n);
for ( int i = 2; i <= n; i ++) if (s[i] <= 0) f[i][i][1][0] = 1;
if (s[1] <= 0) f[1][1][0][1] = 1;
for ( int i = 0; i <= n; i ++) f[i + 1][i][0][0] = 1;
for ( int len = 2; len <= n; len ++) {
for ( int l = 1; l + len - 1 <= n; l ++) {
int r = l + len - 1;
for ( int k = l; k <= r; k ++) {
int c = C(r - l, k - l);
if (s[k] == -1) {
for ( int x = 0; x < M; x ++)
for ( int b = 0; b < M; b ++) {
int sum1 = 0, sum2 = 0;
for ( int y = 0; y < M; y ++) sum1 = add(sum1, f[l][k - 1][x][y]);
for ( int a = 0; a < M; a ++) sum2 = add(sum2, f[k + 1][r][a][b]);
int opl = (w(l, r, k) == l - 1), opr = (w(l, r, k) == r + 1);
f[l][r][x + opl][b + opr] = add(f[l][r][x + opl][b + opr], 1ll * sum1 * sum2 % mod * c % mod);
}
} else {
for ( int y = 0; y < M; y ++) {
int a = s[k] - y;
if (a < 0 || a >= M) continue ;
int opl = (w(l, r, k) == l - 1), opr = (w(l, r, k) == r + 1);
for ( int x = 0; x < M; x ++)
for ( int b = 0; b < M; b ++)
f[l][r][x + opl][b + opr] = add(f[l][r][x + opl][b + opr], 1ll * f[l][k - 1][x][y] * f[k + 1][r][a][b] % mod * c % mod);
}
}
}
}
}
cout << f[1][n][1][0] << '\n';
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int t; cin >> t;
while (t --) solve();
return 0;
}
[HNOI2015] 落忆枫音
首先考虑如何求一个有根 DAG 的生成树数量。
不难发现其实就是除根外的所有点的入度的乘积，相当于给除根外的每个点定一个父亲。
那么加上一条变后，图上肯定会多出若干个环，就要考虑减去包含环的个数。
这里记除根外的所有点的入度的乘积为 \(all\)。
假如知道了一个环，环上点集为 \(S\)，那么包含这个环的个数就是 \(\dfrac{all}{\prod_{i\in S}in_i}\)（这里 \(in_i\) 是点 \(i\) 的入度）。
显然答案就是 \(all-\sum_{S}\dfrac{all}{\prod_{i\in S}in_i}\)。
考虑如何求 \(\sum_{S}\dfrac{all}{\prod_{i\in S}in_i}\)。
因为是在 \((x,y)\) 上加边，那么添加的环也就是 \(y\to x\) 的所有路径加上 \((x,y)\) 这条边。
那么可以从 \(y\) 开始原图上拓扑进行 dp。
记点集 \(T\) 为 \(y\to u\) 的一条路径上的所有点，那么 \(f_u\) 就是 \(\sum_T\dfrac{all}{\prod_{i\in T}in_i}\)。
转移是很简单的，\(f_v=\sum_{(u,v)}f_u\times \dfrac{1}{in_v}\)，初始化 \(f_y=\dfrac{all}{in_y}\)。
最后注意，如果添加的边为 \((x,1)\)，那么答案就是 \(all\)，因为求的是根为 \(1\) 的生成树数量。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 1e9 + 7;
int n, m, x, y;
vector< int> G[N];
int in[N], fin[N];
int f[N];
int ksm( int a, int b, int res = 1) {
while (b) {
if (b & 1) res = 1ll * res * a % mod;
a = 1ll * a * a % mod, b >>= 1;
}
return res;
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m >> x >> y;
in[y] ++;
for ( int i = 1; i <= m; i ++) {
int u, v; cin >> u >> v;
G[u].push_back(v);
in[v] ++, fin[v] ++;
}
int all = 1;
for ( int i = 2; i <= n; i ++) all = 1ll * all * in[i] % mod;
if (y == 1) {
cout << all << '\n';
return 0;
}
queue< int> q;
q.push(1);
while (q.size()) {
int u = q.front(); q.pop();
if (u == y) f[y] = 1ll * all * ksm(in[y], mod - 2) % mod;
for ( auto v : G[u]) {
if (! -- fin[v]) q.push(v);
f[v] = (f[v] + 1ll * f[u] * ksm(in[v], mod - 2) % mod) % mod;
}
}
cout << (all - f[x] + mod) % mod << '\n';
return 0;
}
无向图三元环计数
有一个 \(O(n^2)\) 的做法，先枚举 \(u\) 相连的所有点，并且打上标记。然后枚举与 \(u\) 相连的点 \(v\)，再枚举与 \(v\) 相连的点 \(w\)，如果 \(w\) 被打了标记，那么 \((u,v,w)\) 构成一个三元环。
考虑优化这个过程，发现每次都要枚举完 \(v\) 每一条边，很亏。
有什么办法可以减少枚举次数呢？可以给无向图定向，考虑度数大的点连向度数小的（如果度数相等则编号大的连向编号小的）。
这样一个三元环 \((u,v,w)\) 则一定可以表示成 \(u\to v\)、\(u\to w\)、\(v\to w\) 这样的形式。
但是感觉枚举复杂度并没有减少啊，但其实定完向后再枚举的复杂度是 \(O(m\sqrt m)\) 的。
考虑证明，如果 \(v\) 的度数 \(\le \sqrt m\)，那么 \(v\) 的出边一定是 \(\le\sqrt m\) 的，所以枚举 \(v\to w\) 的复杂度就是 \(\sqrt m\)。
如果 \(v\) 的度数 \(\gt \sqrt m\)，因为所有点的度数和是 \(2m\)，所以度数 \(\gt\sqrt m\) 的点的数量不会超过 \(\sqrt m\) 个，所以枚举 \(u\to v\) 的复杂度是 \(O(\sqrt m)\) 的。
所以总复杂度是 \(O(m\sqrt m)\)。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 998244353;
int n, m;
int deg[N];
int u[N], v[N];
int vis[N];
vector< int> G[N];
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for ( int i = 1; i <= m; i ++) {
cin >> u[i] >> v[i];
deg[u[i]] ++, deg[v[i]] ++;
}
for ( int i = 1; i <= m; i ++) {
int u = :: u[i], v = :: v[i];
if (deg[u] < deg[v]) swap(u, v);
else if (deg[u] == deg[v] && u < v) swap(u, v);
G[u].push_back(v);
}
long long ans = 0;
for ( int u = 1; u <= n; u ++) {
for ( auto v : G[u]) vis[v] = 1;
for ( auto v : G[u])
for ( auto w : G[v]) if (vis[w]) ans ++;
for ( auto v : G[u]) vis[v] = 0;
}
cout << ans << '\n';
return 0;
}
CF2146F Bubble Sort
首先，对于冒泡排序的轮数，有一个结论。
设 \(f_i\) 为在 \([1,i)\) 中，比 \(i\) 位置上的数大的数的个数，那么冒泡排序的轮数就为 \(\max f_i\)，且一种 \(f\) 唯一对应一种排列。
所以可以考虑数所有 \(f\) 的数量，就可以得到所有排列数量。
题目中的 \(b_i\) 就是 \(f\) 的前缀最大值，所以 \(b_i\) 单调递增。
考虑如何刻画这个限制，如果有 \(y\) 个 \(b\) 都 \(\le k\)，那么 \(b_y\) 一定是 \(\le k\) 的，因为它单调递增。
所以要满足 \(\le k\) 的 \(b\) 的个数 \(\ge l\)，其实就是 \(b\) 的 \([1,l]\) 这个前缀都要 \(\le k\)，也就是 \(f\) 的 \([1,l]\) 这个前缀都要 \(\le k\)，可以把这个限制记为 \((l,k)\)。
然后考虑 \(\le r\) 的限制，可以考虑容斥，将 \(\le r\) 的限制变成 \(\ge r + 1\)，就可以记为 \((r+1,k)\)，容斥系数为 \(-1\)。
具体如何操作呢？
考虑把限制按照 \(k\) 从小到大排序，此时可以发现，如果一个前缀 \([1,x]\) 已经被限制 \(\le k\) 了，那么下一个限制 \((x',k')\) 只需要满足 \((x,x']\le k'\)，因为 \([1,x]\) 一定是 \(\le k'\) 的。
所以可以考虑 dp。
设 \(dp_{i,j}\) 表示当前是第 \(i\) 个限制，\([1,j]\) 的前缀都被限制了的方案数。
记当前限制为 \((x,k)\)。
若 \(x\le j\)，那么有 \(dp_{i,j}\leftarrow dp_{i-1,j}\)。
否则就要限制 \((j,x]\le k\)，所以有 \(dp_{i,x}\leftarrow dp_{i-1,j}\times\prod_{p=j+1}^x\min(p,k+1)\)（这里和 \(p\) 取最小值是因为要满足 \(0\le f_p\lt p\)）。
这里单次转移可以预处理阶乘、阶乘逆元和使用快速幂做到 \(O(\log n)\)。
把 \(dp_{i,j}\) 的第二维离散化，复杂度 \(O(m^2\log n)\)。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 1e6 + 10, M = 1e3 + 10, inf = 1e9, mod = 998244353;
int add( int x, int v) {
x += v;
return x >= mod ? x - mod : x;
}
int n, m;
struct lim {
int k, l, r;
} q[M];
int ind[2 * M], tot;
int fac[N], inv[N];
int f[2 * M], g[2 * M];
int ID( int x) {
return lower_bound(ind + 1, ind + tot + 1, x) - ind;
}
int ksm( int a, int b, int res = 1) {
while (b) {
if (b & 1) res = 1ll * res * a % mod;
a = 1ll * a * a % mod, b >>= 1;
}
return res;
}
int cal( int l, int r, int k) {
if (k >= r) {
return 1ll * fac[r] * inv[l] % mod;
} else if (k <= l) {
return ksm(k, r - l);
} else {
return 1ll * ksm(k, r - k) * fac[k] % mod * inv[l] % mod;
}
}
void solve() {
cin >> n >> m;
tot = 0, ind[++ tot] = 0;
for ( int i = 1; i <= m; i ++) {
cin >> q[i].k >> q[i].l >> q[i].r, q[i].r += 1;
ind[++ tot] = q[i].l;
if (q[i].r <= n) ind[++ tot] = q[i].r;
}
sort(q + 1, q + m + 1, [&]( lim a, lim b) {
return a.k < b.k;
});
sort(ind + 1, ind + tot + 1), tot = unique(ind + 1, ind + tot + 1) - ind - 1;
f[1] = 1;
for ( int o = 1; o <= m; o ++) {
int k = q[o].k, l = q[o].l, r = q[o].r;
for ( int i = 1; i <= tot; i ++) g[i] = 0;
int L = ID(l), R = ID(r);
for ( int i = 1; i <= tot; i ++) {
if (ind[i] < l)
g[L] = add(g[L], 1ll * f[i] * cal(ind[i], l, k + 1) % mod);
else g[i] = add(g[i], f[i]);
if (r > n) continue ;
if (ind[i] < r)
g[R] = add(g[R], add(-1ll * f[i] * cal(ind[i], r, k + 1) % mod, mod));
else g[i] = add(g[i], mod - f[i]);
}
for ( int i = 1; i <= tot; i ++) f[i] = g[i];
}
int ans = 0;
for ( int i = 1; i <= tot; i ++)
ans = add(ans, 1ll * f[i] * cal(ind[i], n, n) % mod), f[i] = 0;
cout << ans << '\n';
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
inv[0] = fac[0] = 1;
for ( int i = 1; i < N; i ++) fac[i] = 1ll * fac[i - 1] * i % mod, inv[i] = ksm(fac[i], mod - 2);
int T; cin >> T;
while (T --) solve();
return 0;
}
赢家
考虑全部方案减去 \(1\) 连通的点与 \(2\) 连通的点无交的方案数。
设 \(f_S\) 为 \(S\) 中的点与 \(1\) 连通的方案数，\(g_S\) 为 \(S\) 中的点与 \(2\) 连通的方案数。
记 \(Se_S\) 为 \(S\) 的导出子图中的边数，\(Te_S\) 为只有一个端点在 \(S\) 中的边的个数。
求 \(f_S\)，考虑容斥，初始 \(f_S=2^{Se_S}\)，考虑枚举 \(S\) 的子集 \(S'\)，然后容斥掉只和 \(S'\) 中的点连通的方案数。
转移有：
也就是说所有连向 \(S'\) 的边都要指向 \(S'\)（不然就会往外扩展），其余的边随便方向。
对于 \(g_S\) 来说，求法同理。
然后考虑怎么计算 \(1\) 连通的点与 \(2\) 连通的点无交的方案数。
记 \(S\) 表示与 \(1\) 连通的点，\(T\) 表示与 \(2\) 连通的点。
考虑枚举 \(S\)，那么要满足 \(S\) 和 \(T\) 之间没有边相连，所以可以把 \(S\) 中的点走一条边可以到达的点集 \(S'\) 处理出来，那么 \(T\) 就是 \(U\backslash S'\) 的任意一个子集。
那么方案数就是：
复杂度 \(O(3^n)\)。
代码
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 17, M = 2e5 + 10, inf = 1e9, mod = 1e9 + 7;
int n, m;
struct edge {
int u, v;
} E[N * N];
int f[1 << 17], g[1 << 17];
int Se[1 << 17], Te[1 << 17];
int pw[N * N];
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
pw[0] = 1;
for ( int i = 1; i <= m; i ++) {
int u, v; cin >> u >> v;
E[i] = {u - 1, v - 1};
pw[i] = 2ll * pw[i - 1] % mod;
}
for ( int S = 0; S < (1 << n); S ++) {
for ( int i = 1; i <= m; i ++) {
auto [u, v] = E[i];
int opu = ((S >> u) & 1), opv = ((S >> v) & 1);
if (opu & opv) Se[S] ++;
if (opu ^ opv) Te[S] ++;
}
}
f[1] = 1;
for ( int S = 3; S < (1 << n); S ++) {
if (! (S & 1)) continue ;
f[S] = pw[Se[S]];
for ( int s = S - 1; s; s = (s - 1) & S)
f[S] = (f[S] - 1ll * f[s] * pw[Se[S ^ s]] % mod + mod) % mod;
}
g[2] = 1;
for ( int S = 3; S < (1 << n); S ++) {
if (! ((S >> 1) & 1)) continue ;
g[S] = pw[Se[S]];
for ( int s = S - 1; s; s = (s - 1) & S)
g[S] = (g[S] - 1ll * g[s] * pw[Se[S ^ s]] % mod + mod) % mod;
}
int ans = 0;
for ( int S = 1; S < (1 << n); S ++) {
int T = S;
for ( int i = 1; i <= m; i ++) {
auto [u, v] = E[i];
int opu = ((S >> u) & 1), opv = ((S >> v) & 1);
if (opu ^ opv) T |= (1 << u) | (1 << v);
}
T = ((1 << n) - 1) ^ T;
for ( int t = T; t; t = (t - 1) & T)
ans = (ans + 1ll * f[S] * g[t] % mod * pw[m - Se[S] - Se[t] - Te[S] - Te[t]] % mod) % mod;
}
cout << (pw[m] - ans + mod) % mod << '\n';
return 0;
}
[BalticOI 2024] Wall
容易知道，在确定高度的情况下，记 \(h_i\) 为 \(i\) 位置的高度、\(pre_i\) 为前缀高度最大值、\(suf_i\) 为后缀高度最大值，答案是：\(\sum \min(pre_i,suf_i)-h_i\)。
对于 \(\sum h_i\)，这个很好计算，为 \(2^{n-1}(a_i+b_i)\)。
对于 \(\sum\min(pre_i,suf_i)\)，发现又有最小值，又有最大值，不好处理，所以考虑把 \(\min\) 给拆开。
就有 \(\sum pre_i+suf_i-\max(pre_i,suf_i)\)。
发现后者就是整体最大值，也就是 \(pre_n\)（或者 \(suf_1\)）。
考虑对这三个东西分别求解。
这里先约定，如果有多个最大值，取第一个出现的为最大值，这是为了防止算重。
对于 \(\sum pre_i\)，考虑枚举一个 \(i\) 和一个 \(j\)，表示 \(pre_j\) 是 \(i\) 的值时的贡献。
枚举 \(i\) 的取值 \(h_i\)（\(h_i=a_i\) 或 \(h_i=b_i\)）。
对于 \(1\sim i-1\) 上的值，要满足都小于 \(h_i\)，方案数为 \(\prod_{k=1}^{i-1}([a_k\lt h_i]+[b_k\lt h_i])\)。
对于 \(i+1\sim j\) 上的值，要满足都小于等于 \(h_i\)，方案数为 \(\prod_{k=i+1}^j([a_k\le h_i]+[b_k\le h_i])\)。
对于 \(j+1\sim n\) 上的值，它们没有限制，可以随便选，方案数为 \(2^{n-j}\)。
所以当 \(pre_j\) 是 \(i\) 的值时，它的贡献是：
对于 \(\sum suf_i\)，与 \(\sum pre_i\) 同理，只需把 \(a\)、\(b\) 数组反转即可。
对于 \(\sum pre_n\)，考虑 \(i\) 的值为 \(pre_n\) 时的贡献。
枚举 \(i\) 的取值 \(h_i\)（\(h_i=a_i\) 或 \(h_i=b_i\)）。
对于 \(1\sim i-1\) 上的值，要满足都小于 \(h_i\)，方案数为 \(\prod_{k=1}^{i-1}([a_k\lt h_i]+[b_k\lt h_i])\)。
对于 \(i+1\sim n\) 上的值，要满足都小于等于 \(h_i\)，方案数为 \(\prod_{k=i+1}^n([a_k\le h_i]+[b_k\le h_i])\)。
所以当 \(pre_n\) 是 \(i\) 的值时，它的贡献是：
最后乘 \(n\) 是因为在序列中随意选一个 \(j\)，都可以满足 \(i\) 上的值为 \(pre_n\)，\(j\) 有 \(n\) 中选法。
现在对于上述计算，可以 \(O(n^2)\) 暴力做。
考虑如何优化。
把所有值给存下来，然后从小到大枚举值，当前枚举的值就是 \(h_i\)。
然后开两颗线段树，第一个线段树对每个位置 \(k\) 维护 \([a_k\lt h_i]+[b_k\lt h_i]\) 的值，第二个线段树对每个位置 \(k\) 维护 \([a_k\le h_i]+[b_k\le h_i]\)。
因为是从小到大枚举 \(h_i\)，所以可以用一个指针去扫 \(\lt h_i\) 或 \(\le h_i\) 的所有值，然后线段树修改，均摊下来是 \(O(n\log n)\)。
在每颗线段树上维护一个区间乘积和区间前缀乘积之和，对着式子改成线段树即可。
代码
#include <bits/stdc++.h>
// #define int long long
#define ls k << 1
#define rs k << 1 | 1
#define mid ((l + r) >> 1)
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 5e5 + 10, M = 2e5 + 10, inf = 1e9, mod = 1e9 + 7;
int n, ans;
int a[N], b[N];
int add( int x, int v) {
x += v;
return x >= mod ? x - mod : x;
}
int pw[N];
struct sgt {
int mul, sum;
} ;
struct Sgt {
sgt tr[N * 4];
sgt merge( sgt a, sgt b) {
return {1ll * a.mul * b.mul % mod, add(a.sum, 1ll * a.mul * b.sum % mod)};
}
void clear( int k = 1, int l = 1, int r = n) {
tr[k] = {0, 0};
if (l == r) return ;
clear(ls, l, mid), clear(rs, mid + 1, r);
}
void upd( int x, int v1, int v2, int k = 1, int l = 1, int r = n) {
if (l == r) return tr[k] = {v1, v2}, void();
x <= mid ? upd(x, v1, v2, ls, l, mid) : upd(x, v1, v2, rs, mid + 1, r);
tr[k] = merge(tr[ls], tr[rs]);
}
sgt ask( int x, int y, int k = 1, int l = 1, int r = n) {
if (x > y) return {1, 0};
if (x <= l && r <= y) return tr[k];
if (y <= mid) return ask(x, y, ls, l, mid);
if (x > mid) return ask(x, y, rs, mid + 1, r);
return merge(ask(x, y, ls, l, mid), ask(x, y, rs, mid + 1, r));
}
} T1, T2;
struct node {
int val, i, op;
} ;
struct que {
int val, i;
} ;
vector< node> vec;
vector< que> query;
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
for ( int i = 1; i <= n; i ++) cin >> a[i];
for ( int i = 1; i <= n; i ++) cin >> b[i];
for ( int i = 1; i <= n; i ++) {
if (a[i] > b[i]) swap(a[i], b[i]);
vec.push_back({a[i], i, 1});
vec.push_back({b[i], i, 2});
}
for ( int i = 1; i <= n; i ++)
for ( int h : {a[i], b[i]})
query.push_back({h, i});
sort(vec.begin(), vec.end(), [&]( node a, node b) {
return a.val < b.val;
});
sort(query.begin(), query.end(), [&]( que a, que b) {
return a.val < b.val;
});
pw[0] = 1;
for ( int i = 1; i <= n; i ++) pw[i] = 2ll * pw[i - 1] % mod;
int sumh = 0, sump = 0, sums = 0, sumn = 0;
for ( int i = 1; i <= n; i ++)
sumh = add(sumh, 1ll * pw[n - 1] * (a[i] + b[i]) % mod);
ans = add(ans, mod - sumh);
T1.clear(), T2.clear();
int ptr1 = 0, ptr2 = 0;
for ( auto q : query) {
while (vec[ptr1].val < q.val && ptr1 < vec.size()) {
T1.upd(vec[ptr1].i, vec[ptr1].op, 1ll * vec[ptr1].op * pw[n - vec[ptr1].i] % mod);
ptr1 ++;
}
while (vec[ptr2].val <= q.val && ptr2 < vec.size()) {
T2.upd(vec[ptr2].i, vec[ptr2].op, 1ll * vec[ptr2].op * pw[n - vec[ptr2].i] % mod);
ptr2 ++;
}
int res1 = T1.ask(1, q.i - 1).mul, res2 = T2.ask(q.i + 1, n).mul;
sumn = add(sumn, 1ll * q.val * n % mod * res1 % mod * res2 % mod);
}
ans = add(ans, mod - sumn);
T1.clear(), T2.clear();
ptr1 = 0, ptr2 = 0;
for ( auto q : query) {
while (vec[ptr1].val < q.val && ptr1 < vec.size()) {
T1.upd(vec[ptr1].i, vec[ptr1].op, 1ll * vec[ptr1].op * pw[n - vec[ptr1].i] % mod);
ptr1 ++;
}
while (vec[ptr2].val <= q.val && ptr2 < vec.size()) {
T2.upd(vec[ptr2].i, vec[ptr2].op, 1ll * vec[ptr2].op * pw[n - vec[ptr2].i] % mod);
ptr2 ++;
}
int res1 = T1.ask(1, q.i - 1).mul;
sump = add(sump, 1ll * q.val * res1 % mod * pw[n - q.i] % mod);
int res2 = T2.ask(q.i + 1, n).sum;
sump = add(sump, 1ll * q.val * res1 % mod * res2 % mod);
}
ans = add(ans, sump);
reverse(a + 1, a + n + 1);
reverse(b + 1, b + n + 1);
vec.clear(), query.clear();
for ( int i = 1; i <= n; i ++) {
vec.push_back({a[i], i, 1});
vec.push_back({b[i], i, 2});
}
for ( int i = 1; i <= n; i ++)
for ( int h : {a[i], b[i]})
query.push_back({h, i});
sort(vec.begin(), vec.end(), [&]( node a, node b) {
return a.val < b.val;
});
sort(query.begin(), query.end(), [&]( que a, que b) {
return a.val < b.val;
});
T1.clear(), T2.clear();
ptr1 = 0, ptr2 = 0;
for ( auto q : query) {
while (vec[ptr1].val < q.val && ptr1 < vec.size()) {
T1.upd(vec[ptr1].i, vec[ptr1].op, 1ll * vec[ptr1].op * pw[n - vec[ptr1].i] % mod);
ptr1 ++;
}
while (vec[ptr2].val <= q.val && ptr2 < vec.size()) {
T2.upd(vec[ptr2].i, vec[ptr2].op, 1ll * vec[ptr2].op * pw[n - vec[ptr2].i] % mod);
ptr2 ++;
}
int res1 = T1.ask(1, q.i - 1).mul;
sums = add(sums, 1ll * q.val * res1 % mod * pw[n - q.i] % mod);
int res2 = T2.ask(q.i + 1, n).sum;
sums = add(sums, 1ll * q.val * res1 % mod * res2 % mod);
}
ans = add(ans, sums);
cout << ans << '\n';
return 0;
}
排列幂
没有原题。
\(n\le 5000,m\le 10^{10000}\)。
首先知道，排列的排名为 \(\sum_{i\lt j}[p_i\gt p_j](n-i)!\)。
对于排列的置换题目，考虑把环建出来，但因为求贡献需要同时知道 \(i\) 和 \(j\)，所以考虑把 \((i,j)\) 看作一个点，把环建出来。容易知道所有环长之和为 \(O(n^2)\)。
把环建出来后，考虑怎么求贡献。
首先，把满足 \(i\lt j\) 的点 \((i,j)\) 看作起点，它的权值为 \(0\)，那么满足 \(i\gt j\) 的点 \((i,j)\)，它的权值就是 \(1\)（这里对应了 \([p_i\gt p_j]\)）。
所以问题转化成，从环上权值为 \(0\) 的点出发，走 \(m\) 步（初始为第一步），记走过的所有点的权值和为 \(sum\)，那么这个点 \((i,j)\) 的贡献就是 \(sum\times (n-i)!\)。
记环长为 \(L\)，那么会绕着环走 \(\frac{m}{L}\) 圈，再走上 \(m\bmod L\) 步。
因为 \(m\) 很大，所以写一个高精除法即可，对于 \(sum\)，可以用前缀和快速计算。
最后复杂度为 \(O(n^2)\)。
代码
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
void Freopen() {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
using namespace std;
const int N = 5e3 + 10, M = 2.5e7 + 10, inf = 1e9, mod = 998244353;
int n;
int p[N];
int sum[M];
bitset< N> vis[N];
int cnt;
vector< pair< int, int> > cle;
char m[10010];
int lth;
void dfs( int x, int y) {
if (vis[x][y]) return ;
vis[x][y] = 1;
cle.push_back({x, (x > y)});
dfs(p[x], p[y]);
}
unordered_map< int, pair< int, int> > mp;
pair< int, int> cal( int L) {
if (mp.count(L)) return mp[L];
long long res = 0, md = 0;
for ( int i = 1; i <= lth; i ++) {
md = md * 10 + (m[i] - '0');
res = res * 10 % mod;
if (md >= L) res = (res + md / L) % mod, md %= L;
}
return (mp[L] = {res, md});
}
int fac[N];
signed main() {
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> (m + 1);
lth = strlen(m + 1);
for ( int i = 1; i <= n; i ++) cin >> p[i];
fac[0] = 1;
for ( int i = 1; i <= n; i ++) fac[i] = 1ll * fac[i - 1] * i % mod;
int ans = 0;
for ( int x = 1; x <= n; x ++)
for ( int y = 1; y <= n; y ++) {
if (x == y || vis[x][y]) continue ;
cle.clear();
dfs(x, y);
int len = (int)cle.size();
for ( int i = 0; i < len; i ++) cle.push_back(cle[i]);
auto [res, md] = cal(len);
sum[0] = cle[0].second;
for ( int i = 1; i < 2 * len; i ++) sum[i] = sum[i - 1] + cle[i].second;
for ( int i = 0; i < len; i ++) {
if (cle[i].second == 0) {
ans = (ans + 1ll * sum[len - 1] * fac[n - cle[i].first] % mod * res % mod) % mod;
if (md) {
ans = (ans + 1ll * fac[n - cle[i].first] * (sum[i + md - 1] - (i ? sum[i - 1] : 0)) % mod) % mod;
}
}
}
}
auto [res, md] = cal(1);
cout << (ans + res) % mod << '\n';
// 记得最后加 $m$，因为本质上计算的是比这个排列小的排列数量，所以排名要加一。
return 0;
}
浙公网安备 33010602011771号