字符串整理
制糊串整理(持续更新ing)
发现字符串部分真的是空白啊!
那就从头开始吧
(刚考完合格考,终于有时间了qwq)
Manacher算法
找回文串的,大家都知道。
然后注意一点就是这个只能找到长度为奇数的回文串,所以我们得在两个字符之间补充一个字符,最前面也需要补充一个字符。
Manacher原理就是利用他的对称性,如果一个大的串对称,那么如果前半部分有回文串,后半部分相应位置也应该有。
注意到时间复杂度跟暴力扩展判断的次数有关,每次扩展都会使得\(r+1\),显然复杂度是线性的。
cin>>(s+1);
int len=strlen(s+1);
t[0]='!';
t[++tot]='&';
for(int i=1;i<=len;i++) t[++tot]=s[i],t[++tot]='&';
t[++tot]='%';
for(int i=1,r=0,d=0;i<=tot;i++){
if(i>r) p[i]=1;else p[i]=min(p[2*d-i],r-i+1);
while(t[i+p[i]]==t[i-p[i]]) p[i]++;
if(i+p[i]-1>r) r=i+p[i]-1,d=i;
}
来几个例题吧
P4555 [国家集训队] 最长双回文串
处理出来以每个位置结尾,开头的最长回文串长度,然后求个\(max(ed_i+st_{i+1})\)就完事了
#include<bits/stdc++.h>
#define rep(i,a,n) for(int i=a;i<=n;++i)
#define per(i,a,n) for(int i=n;i>=a;--i)
#define N(x,y) ((int)((int)(x##e##y)+5))
using namespace std;
char s[N(6,5)],t[N(6,5)];
int n,m;
int p[N(6,5)],l[N(6,5)],r[N(6,5)];
signed main(){
cin>>(s+1);
t[0]='!';
n=strlen((s+1));
t[m=1]='@';
rep(i,1,n)t[++m]=s[i],t[++m]='@';
t[++m]='&';
int d=0,rr=0;
rep(i,1,m){
if(i>rr) p[i]=1;else p[i]=min(rr-i+1,p[2*d-i]);
while(t[i+p[i]]==t[i-p[i]]) p[i]++;
if(i+p[i]-1>rr){
rep(j,rr+1,i+p[i]-1){
if(j%2==0)l[j>>1]=j-i+1;
}
rr=i+p[i]-1,d=i;
}
}
d=0,rr=m;
per(i,1,m-1){
if(i<rr) p[i]=1;else p[i]=min(i-rr+1,p[2*d-i]);
while(t[i+p[i]]==t[i-p[i]]) p[i]++;
if(i-p[i]+1<rr){
rep(j,i-p[i]+1,rr-1){
if(j%2==0)r[j>>1]=i-j+1;
}
rr=i-p[i]+1,d=i;
}
}
int ans=0;
rep(i,1,n-1){
ans=max(ans,l[i]+r[i+1]);
}
cout<<ans;
return 0;
}
P1659 [国家集训队] 拉拉队排练
属于\([1,p_i-1]\)的所有回文长度都存在,所以直接进行差分,最后对每一种长度的个数快速幂计算一下即可。
#include<bits/stdc++.h>
#define rep(i,a,n) for(int i=a;i<=n;++i)
#define per(i,a,n) for(int i=n;i>=a;--i)
#define N(x,y) ((int)((int)(x##e##y)+5))
#define i64 long long
using namespace std;
inline i64 read(){
i64 x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int mod=19930726;
i64 qpow(int a,int b){
i64 res=1;
while(b){
if(b&1) res=1ll*res*a%mod;
a=1ll*a*a%mod;
b>>=1;
}
return res;
}
char s[N(2,6)],t[N(2,6)];
i64 n,m,k;
i64 p[N(1,6)],buk[N(1,6)];
signed main(){
n=read(),k=read();
cin>>(s+1);
n=strlen((s+1));
s[0]='!';
int d=0,rr=0;
rep(i,1,n){
if(i>rr) p[i]=1;else p[i]=min(1ll*(rr-i+1),p[2*d-i]);
while(s[i+p[i]]==s[i-p[i]]) p[i]++;
buk[1]++,buk[2*p[i]+1]--;
if(i+p[i]-1>rr){
rr=i+p[i]-1,d=i;
}
}
int mx=0;
rep(i,1,n){
buk[i]+=buk[i-1];
if(buk[i]){
mx=max(mx,i);
}
}
i64 ans=1;
i64 pt=mx;
while(k){
if(k<=0||pt<=0) break;
if(pt%2==0) {pt--;continue;}
ans=1ll*ans*qpow(pt,min(buk[pt],k))%mod;
k-=min(buk[pt],k);
pt--;
}
cout<<ans;
return 0;
}
P5446 [THUPC2018] 绿绿和串串
首先以\(n\)结尾的回文串都合法,然后所有结尾位置为一个合法位置且以\(1\)开头的回文串也都合法,然后就从后往前扫依次判断就好了。
#include<bits/stdc++.h>
#define i64 long long
using namespace std;
int n,p[5000005],vis[5000005];
void solve(){
string a;
cin>>a;
a.push_back('!');
reverse(a.begin(),a.end());
n=(int)a.size()-1;
for(int i=1;i<=n;i++){
vis[i]=0;
}
for(int i=1,d=0,r=0;i<=n;i++){
if(i>r) p[i]=1; else p[i]=min(p[2*d-i],r-i+1);
while(a[i+p[i]]==a[i-p[i]]) p[i]++;
if(i+p[i]-1>r) r=i+p[i]-1,d=i;
}
for(int i=1;i<=n;i++){
if(i-p[i]+1==1)vis[i]=1;
if(i+p[i]-1==n&&vis[2*i-n]) vis[i]=1;
}
for(int i=n;i>=1;i--){
if(vis[i]) cout<<n-i+1<<" ";
}
putchar(10);
}
signed main(){
int tt;
tt=read();
while(tt--){
solve();
}
}
Pass
后缀数组
这玩意我以前都是纯靠背的/kk
写几个定义吧。
\(su_i\)代表以\(i\)开头的后缀。\(rk_i\)代表\(su_i\)在所有后缀中的排名。\(sa_i\)代表排名为\(i\)的后缀的起始位置,也就是说\(sa_{rk_i}=rk_{sa_i}=i\)。
然后 我们要求的就是\(sa\)数组。
我们可以通过\(2^{w-1}\)级子串的排名\(rk_i\)来推出\(2^w\)级子串的\(sa_i\),我们通过比较\((rk_i,rk_{i+2^{w-1}})\)和\((rk_j,rk_{j+2^{w-1}})\),就可以确定新的\(rk_i\)和\(rk_j\)。
其实有一个常数的优化就是,那些后面不全的后缀,他们比较的时候一定是排在最前面的。
signed main(){
cin>>(s+1);
int m=1<<7,p=0,n=strlen(s+1);
for(int i=1;i<=n;i++) buk[rk[i]=s[i]]++,id[rk[i]]=1;
for(int i=1;i<=m;i++) buk[i]+=buk[i-1],id[i]+=id[i-1];
for(int i=n;i;i--) sa[buk[s[i]]--]=i;
for(int i=1;i<=n;i++) rk[i]=id[s[i]];
for(int w=1;w<=n&&rk[sa[n]]<n;w<<=1,p=0){
for(int i=n-w+1;i<=n;i++) id[++p]=i;
for(int i=1;i<=n;i++) if(sa[i]>w) id[++p]=sa[i]-w;
for(int i=1;i<=n;i++) buk[rk[sa[i]]]=i;
for(int i=n;i;i--) sa[buk[rk[id[i]]]--]=id[i];
for(int i=1;i<=n;i++) id[sa[i]]=id[sa[i-1]]+((rk[sa[i]]!=rk[sa[i-1]])||(rk[sa[i]+w]!=rk[sa[i-1]+w]));
for(int i=1;i<=n;i++) rk[i]=id[i];
}
for(int i=1;i<=n;i++){
cout<<sa[i]<<" ";
}
return 0;
}
刚开始有点看不懂,感觉有几点需要说明一下:
- 为啥是\(sa_i>w\)的时候把\(sa_i-w\)放进去,因为就是相当于把当前这个位置作为第二关键字、它所对应的第一关键字的位置给放进去了(因为你基数排序只比较第一个关键字,\(id\)放进去的时候要按照第二关键字先排好序了)
- 没必要一定要让\(w\)跑满,只要\(rk_{sa_n}=n\)了就说明已经排完序了
然后这里再来一个定义\(ht_i\)代表\(|lcp(su_{sa_i},su_{sa_{i-1}})|\),特别地,有\(ht_1=0\)。
然后有一个性质:$ht_{rk_i}\geq ht_{rk_{i-1}}+1 $
然后怎么证明捏?
我们首先考虑两个分割开的子串
{i-1}{i}{}{}{}{}{}{}{}{}{}{} {p}{p+1}{}{}{}{}{}{}{}{}{}
其中,\(p=sa_{rk_{i-1}-1}\),然后如果\(ht_{rk_{i-1}}>1\)的时候,一定有\(s_i=s_{p+1}\),那么同时也说明\(su_i<su_{p+1}\),也就是说\(lcp(su_i,su_{p+1})=ht_{rk_{i-1}}-1\),然后同时说明排名在\(su_i\)和\(su_{p+1}\)之间的后缀,他们与\(su_i\)之间的\(lcp\)不会变小,因此有\(ht_{rk_i}\geq ht_{rk_{i-1}}+1\)。
那么求\(ht\)的代码就可以这么写。
for(int i=1,k=0;i<=n;i++){
if(k) k--;
while(s[i+k]==s[sa[rk[i]-1]+k]) k++;
ht[rk[i]]=k;
}
由于\(k\)几乎是单调不减的,所以\(k\)不会加超过\(2n\)次,所以是线性的。
然后我们就可以利用\(ht\),求出来任意两个后缀的\(lcp\)。
怎么证明捏:
这里借用一下\(AlexWei\)的例子:
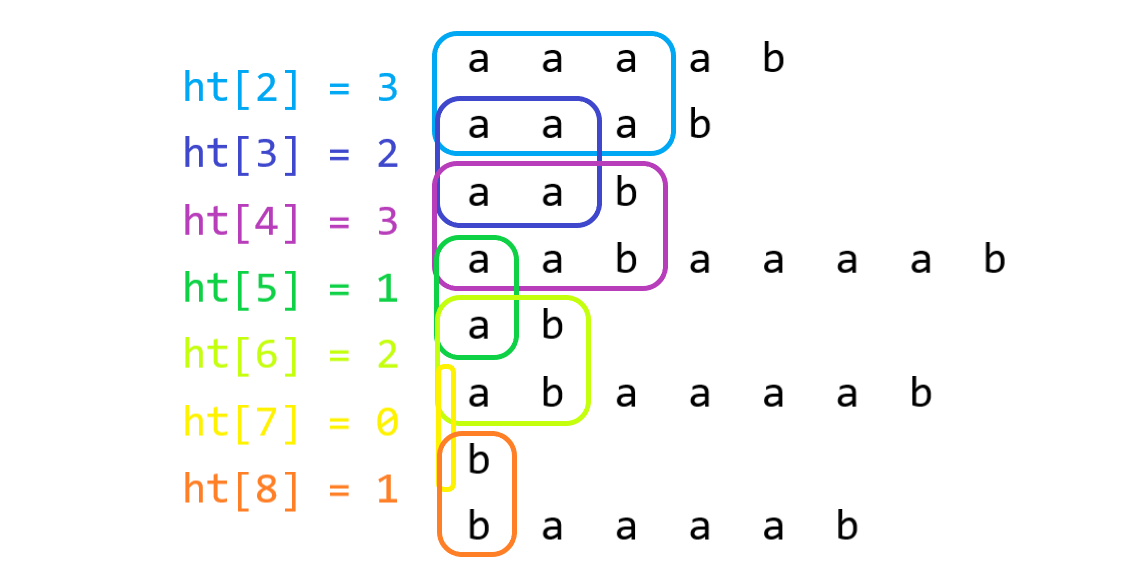
然后我们可以得到两个信息,一个是两个字符串排名相隔距离越大,差别就越大,另外一个是两个字符串之间的\(lcp\)就是他俩之间矩形的最小值。
这样就可以和单调栈结合,或者和ST表结合。
记得特判\(i=j\)的情况。
然后来几个应用!
求本质不同子串个数
我们考虑每次加入一个后缀,然后它的贡献是\(max_{j\in S}|lcp(su_i,su_j)|\),那么显而易见的是\(max_{j \in S}|lcp(su_i,su_j)|=ht_{rk_i}\),那么答案就是\(\frac{n(n+1)}{2}-\sum_{i=2}^{n}ht_i\)。
P2408 不同子串个数
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;char c=getchar();
while(!isdigit(c)){if(c=='-')f-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return x*f;
}
using i64=long long;
const int N=1e6+5;
char s[N];
int id[N],buk[N<<1],rk[N],sa[N],ht[N];
signed main(){
read();
cin>>(s+1);
int m=1<<7,p=0,n=strlen(s+1);
for(int i=1;i<=n;i++) buk[rk[i]=s[i]]++,id[rk[i]]=1;
for(int i=1;i<=m;i++) buk[i]+=buk[i-1],id[i]+=id[i-1];
for(int i=n;i;i--) sa[buk[s[i]]--]=i;
for(int i=1;i<=n;i++) rk[i]=id[s[i]];
for(int w=1;w<=n&&rk[sa[n]]<n;w<<=1,p=0){
for(int i=n-w+1;i<=n;i++) id[++p]=i;
for(int i=1;i<=n;i++) if(sa[i]>w) id[++p]=sa[i]-w;
for(int i=1;i<=n;i++) buk[rk[sa[i]]]=i;
for(int i=n;i;i--) sa[buk[rk[id[i]]]--]=id[i];
for(int i=1;i<=n;i++) id[sa[i]]=id[sa[i-1]]+((rk[sa[i]]!=rk[sa[i-1]])||(rk[sa[i]+w]!=rk[sa[i-1]+w]));
for(int i=1;i<=n;i++) rk[i]=id[i];
}
for(int i=1,k=0;i<=n;i++){
if(k)k--;
while(s[i+k]==s[sa[rk[i]-1]+k]) k++;
ht[rk[i]]=k;
}
i64 ans=1ll*n*(n+1)/2;
for(int i=1;i<=n;i++) ans-=ht[rk[i]];
cout<<ans;
return 0;
}
P1117 [NOI2016] 优秀的拆分
给我整麻了,用到了一个trick就是一个长度为\(2len\)的区间,他必定越过了两个之间长度为\(len\)的点,然后我们就可以先等距离分块,对于每个块里面的合法断点记录一下,差分一下记录答案,然后把答案拆成\(\sum f_ig_i\)的形式,其中\(f_i\)表示正着的\(AA\),\(g_i\)表示倒着的。
#include<bits/stdc++.h>
using namespace std;
using i64=long long;
inline int read(){
int x=0,f=1;char c=getchar();
while(!isdigit(c)){if(c=='-')f-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return x*f;
}
const int N=2e5+5;
int lg[N],f[N],g[N];
struct SA{
char s[N];
int ht[N],sa[N],rk[N],buk[N<<1],id[N],st[N][20],n;
void reset(){memset(s,0,sizeof s);memset(ht,0,sizeof ht);memset(rk,0,sizeof rk);memset(id,0,sizeof id);memset(buk,0,sizeof buk);memset(sa,0,sizeof sa);memset(st,0,sizeof st);}
void build(){
n=strlen(s+1);
int m=1<<7;
for(int i=1;i<=n;i++) buk[rk[i]=s[i]]++,id[rk[i]]=1;
for(int i=1;i<=m;i++) buk[i]+=buk[i-1],id[i]+=id[i-1];
for(int i=n;i;i--) sa[buk[s[i]]--]=i;
for(int i=1;i<=n;i++) rk[i]=id[s[i]];
for(int w=1,p=0;w<=n&&rk[sa[n]]<n;w<<=1,p=0){
for(int i=n-w+1;i<=n;i++) id[++p]=i;
for(int i=1;i<=n;i++) if(sa[i]>w) id[++p]=sa[i]-w;
for(int i=1;i<=n;i++) buk[rk[sa[i]]]=i;
for(int i=n;i;i--) sa[buk[rk[id[i]]]--]=id[i];
for(int i=1;i<=n;i++) id[sa[i]]=id[sa[i-1]]+((rk[sa[i]]!=rk[sa[i-1]])||(rk[sa[i]+w]!=rk[sa[i-1]+w]));
for(int i=1;i<=n;i++) rk[i]=id[i];
}
for(int i=1,k=0;i<=n;i++){
if(k) k--;
while(s[i+k]==s[sa[rk[i]-1]+k]&&k<=n-i) k++;
ht[rk[i]]=k;
}
for(int i=1;i<=n;i++) st[i][0]=ht[i];
for(int j=1;(1<<j)<=n;j++){
for(int i=1;i+(1<<j)-1<=n;i++){
st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
}
}
int lcp(int l,int r){
if(l==r) return n-l+1;
l=rk[l],r=rk[r];
if(r<l) swap(l,r);
l++;
int leg=lg[r-l+1];
return min(st[l][leg],st[r-(1<<leg)+1][leg]);
}
}a,reva;
signed main(){
int tt=read();
lg[0]=-1;
for(int i=1;i<=N-5;i++){
lg[i]=lg[i>>1]+1;
}
lg[0]=0;
while(tt--){
a.reset(),reva.reset();
cin>>(a.s+1);
int n=strlen(a.s+1);
for(int i=1;i<=n;i++) reva.s[i]=a.s[n-i+1];
a.build(),reva.build();
memset(f,0,sizeof f);memset(g,0,sizeof g);
for(int len=1;len<=n/2;len++){
for(int pos=len;pos<=n;pos+=len){
int l=pos,r=pos+len;
int L=n-(l-1)+1,R=n-(r-1)+1;
int lcp=min(len,a.lcp(l,r)),lcs=min(len-1,reva.lcp(L,R));
int t=lcp+lcs-len+1;
if(lcp+lcs>=len){
f[r+lcp-t]++,f[r+lcp]--;
g[l-lcs]++,g[l-lcs+t]--;
}
}
}
i64 ans=0;
for(int i=1;i<=n;i++) f[i]+=f[i-1],g[i]+=g[i-1];
for(int i=1;i<n;i++) ans+=1ll*f[i]*g[i+1];
cout<<ans<<"\n";
}
return 0;
}
P4248 [AHOI2013] 差异
板,发现答案其实就是区间最小值之和,那么根据之前那个图,一眼丁真,鉴定为单调栈。
#include<bits/stdc++.h>
using namespace std;
using i64=long long;
inline int read(){
int x=0,f=1;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return x*f;
}
const int N=5e5+5;
int ht[N],id[N],buk[N],sa[N],rk[N],n,top,stk[N],l[N],r[N];
char s[N];
signed main(){
cin>>(s+1);
n=strlen(s+1);
int m=1<<7;
for(int i=1;i<=n;i++) buk[rk[i]=s[i]]++,id[rk[i]]=1;
for(int i=1;i<=m;i++) buk[i]+=buk[i-1],id[i]+=id[i-1];
for(int i=1;i<=n;i++) sa[buk[s[i]]--]=i;
for(int i=1;i<=n;i++) rk[i]=id[s[i]];
for(int w=1,p=0;rk[sa[n]]<n&&w<=n;w<<=1,p=0){
for(int i=n-w+1;i<=n;i++) id[++p]=i;
for(int i=1;i<=n;i++) if(sa[i]>w) id[++p]=sa[i]-w;
for(int i=1;i<=n;i++) buk[rk[sa[i]]]=i;
for(int i=n;i;i--) sa[buk[rk[id[i]]]--]=id[i];
for(int i=1;i<=n;i++) id[sa[i]]=id[sa[i-1]]+((rk[sa[i-1]]!=rk[sa[i]])||(rk[sa[i-1]+w]!=rk[sa[i]+w]));
for(int i=1;i<=n;i++) rk[i]=id[i];
}
for(int i=1,k=0;i<=n;i++){
if(k) k--;
while(s[i+k]==s[sa[rk[i]-1]+k]&&i+k<=n&&sa[rk[i]-1]+k<=n) k++;
ht[rk[i]]=k;
}
i64 tot=0;
stk[top=1]=1;
for(int i=2;i<=n;i++){
while(top&&ht[stk[top]]>ht[i]) r[stk[top--]]=i;
l[i]=stk[top];
stk[++top]=i;
}
while(top) r[stk[top--]]=n+1;
for(int i=1;i<=n;i++){
tot+=2ll*(r[i]-i)*(i-l[i])*ht[i];
}
i64 ans=1ll*(n-1)*n*(n+1)/2-tot;
cout<<ans;
return 0;
}
P4051 [JSOI2007] 字符加密
板,一眼顶针,鉴定为破环为链。
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,rk[N],sa[N],id[N],buk[N<<1];
char s[N];
signed main(){
cin>>(s+1);
n=strlen(s+1);
for(int i=n+1;i<=2*n;i++) s[i]=s[i-n];
n=2*n;
int m=1<<7;
for(int i=1;i<=n;i++) buk[rk[i]=s[i]]++,id[rk[i]]=1;
for(int i=1;i<=m;i++) buk[i]+=buk[i-1],id[i]+=id[i-1];
for(int i=n;i;i--) sa[buk[s[i]]--]=i;
for(int i=1;i<=n;i++) rk[i]=id[s[i]];
for(int w=1,p=0;w<=n&&rk[sa[n]]<n;w<<=1,p=0){
for(int i=n-w+1;i<=n;i++) id[++p]=i;
for(int i=1;i<=n;i++) if(sa[i]>w) id[++p]=sa[i]-w;
for(int i=1;i<=n;i++) buk[rk[sa[i]]]=i;
for(int i=n;i;i--) sa[buk[rk[id[i]]]--]=id[i];
for(int i=1;i<=n;i++) id[sa[i]]=id[sa[i-1]]+((rk[sa[i]]!=rk[sa[i-1]])||(rk[sa[i]+w]!=rk[sa[i-1]+w]));
for(int i=1;i<=n;i++) rk[i]=id[i];
}
for(int i=1;i<=n;i++) if(sa[i]<=n/2) putchar(s[sa[i]+n/2-1]);
return 0;
}
P3181 [HAOI2016] 找相同字符
虽然好像可以用广义SAM做,但其实我们既然会做上面的“差异”那道题了,我们就会求\(\sum lcp\)了,那其实答案就是两个串拼起来的\(lcp\)减去独立的\(lcp\)。
#include<bits/stdc++.h>
using namespace std;
#define i64 long long
const int m=1<<7,N=4e5+5;
char s1[N],s2[N],t[N];
int buk[N],id[N],rk[N],sa[N],ht[N],stk[N],top,l[N],r[N];
i64 calc(char *s){
memset(buk,0,sizeof buk);
memset(rk,0,sizeof rk);
memset(sa,0,sizeof sa);
memset(id,0,sizeof id);
memset(ht,0,sizeof ht);
memset(l,0,sizeof l);
memset(r,0,sizeof r);
int n=strlen(s+1);
for(int i=1;i<=n;i++) buk[rk[i]=s[i]]++,id[rk[i]]=1;
for(int i=1;i<=m;i++) buk[i]+=buk[i-1],id[i]+=id[i-1];
for(int i=n;i;i--) sa[buk[s[i]]--]=i;
for(int i=1;i<=n;i++) rk[i]=id[s[i]];
for(int w=1,p=0;w<=n&&rk[sa[n]]<n;w<<=1,p=0){
for(int i=n-w+1;i<=n;i++) id[++p]=i;
for(int i=1;i<=n;i++) if(sa[i]>w) id[++p]=sa[i]-w;
for(int i=1;i<=n;i++) buk[rk[sa[i]]]=i;
for(int i=n;i;i--) sa[buk[rk[id[i]]]--]=id[i];
for(int i=1;i<=n;i++) id[sa[i]]=id[sa[i-1]]+((rk[sa[i]]!=rk[sa[i-1]])||(rk[sa[i]+w]!=rk[sa[i-1]+w]));
for(int i=1;i<=n;i++) rk[i]=id[i];
}
for(int i=1,k=0;i<=n;i++){
if(k) k--;
while(s[i+k]==s[sa[rk[i]-1]+k]&&i+k<=n&&sa[rk[i]-1]+k<=n) k++;
ht[rk[i]]=k;
}
i64 ans=0;
stk[top=1]=1;
for(int i=2;i<=n;i++){
while(top&&ht[stk[top]]>ht[i]) r[stk[top--]]=i;
l[i]=stk[top];
stk[++top]=i;
}while(top) r[stk[top--]]=n+1;
for(int i=1;i<=n;i++){
ans+=1ll*(r[i]-i)*(i-l[i])*ht[i];
}
return ans;
}
signed main(){
cin>>(s1+1)>>(s2+1);
int len1=strlen(s1+1),len2=strlen(s2+1);
for(int i=1;i<=len1;i++){
t[i]=s1[i];
}
t[len1+1]='~';
for(int i=len1+2;i<=len1+len2+1;i++){
t[i]=s2[i-len1-1];
}
cout<<calc(t)-calc(s1)-calc(s2);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号