Qt迷宫实现简单的创建和寻路

一，问题描述
- 1，问题描述
- 2，设计功能要求
二，设计思路
三，效果展示
四，部分代码细节
五，其他

一，问题描述

1，问题描述

迷宫实验是取自心理学的一个古典实验。在该实验中，把一只老鼠从一个无顶大盒子的门放入，在盒中设置了许多墙，对行进方向形成了多处阻挡。盒子仅有一个出口，在出口处放置一块奶酪，吸引老鼠在迷宫中寻找道路以到达出口。对同一只老鼠重复进行上述实验，一直到老鼠从入口到出口，而不走错一步。老鼠经多次试验终于得到它学习走迷宫的路线。

2，设计功能要求

迷宫由 m 行 n 列的二维数组设置，0 表示无障碍，1 表示有障碍。设入口为（1，1），出口为（m，n），每次只能从一个无障碍单元移到周围四个方向上任一无障碍单元。编程实现对任意设定的迷宫，求出一条从入口到出口的通路，或得出没有通路的结论。

算法输入：代表迷宫入口的坐标
算法输出：穿过迷宫的结果。
算法要点：创建迷宫，试探法查找路。

二，设计思路

1，迷宫的创建

如何保存？
使用二维数组进行保存，0 代表路，1 代表墙，2 代表起点，3 代表终点
如何创建？
1，手动创建：手动输入二维数组进行创建
2，自动创建：通过使用自然分岔型^[1]进行创建

2，如何寻路

BFS 广度优先搜索
通过创建栈进行寻路
DFS 深度优先搜索
通过创建队列进行寻路

3，如何展示及想要实现的效果

使用Qt创建可视化的迷宫界面
可直接在迷宫界面对迷宫进行修改
将迷宫的通路可视化显示在迷宫界面上，并且有动画效果

三，效果展示

初始界面
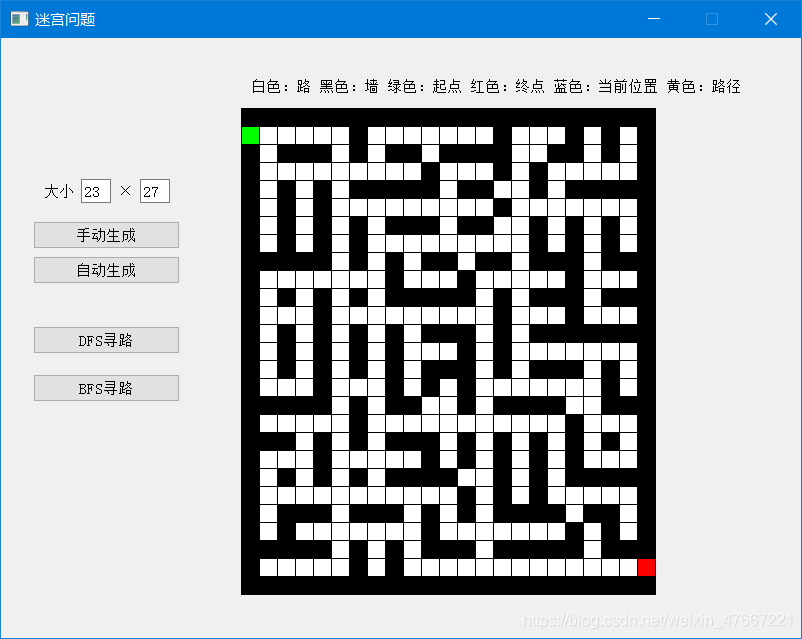
自动创建迷宫（起点和终点须手动设置）
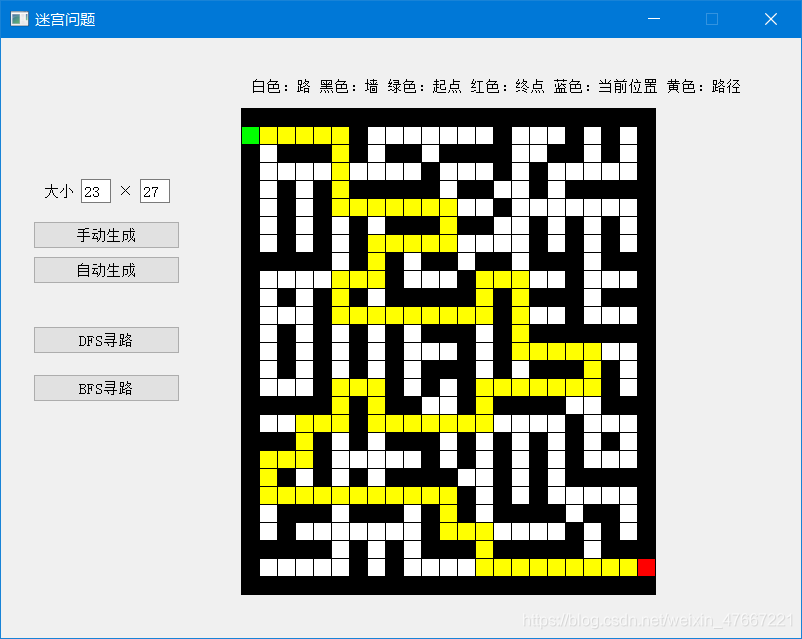
DFS寻路
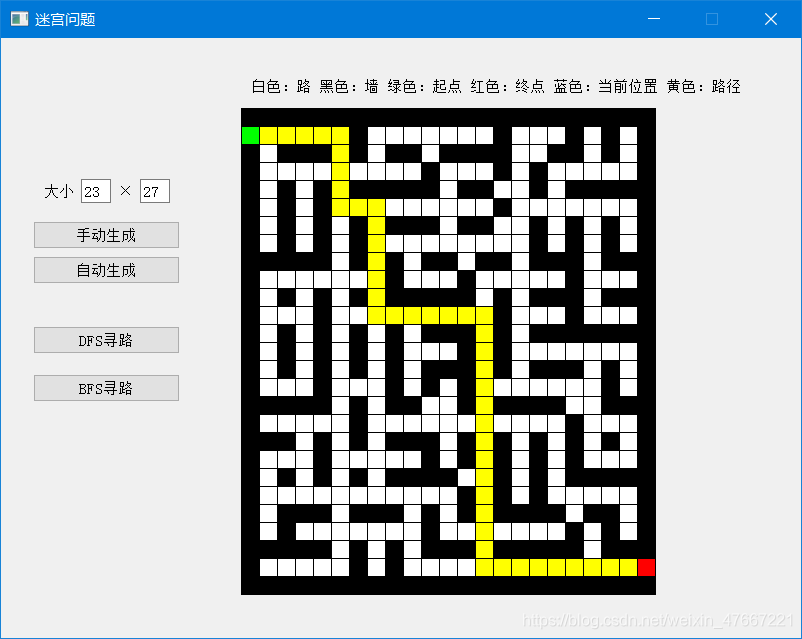
BFS寻路

四，部分代码细节

1，如何在界面上绘制迷宫

我使用 maze_record 保存迷宫原始数据，使用 maze_data 来保存迷宫的其他细节，如果某位置 P(x，y) 已经被访问，则将 maze_data[x][y] 设为 -1，最后绘图时使用 maze_data 的数据

void MyWidget::paintEvent(QPaintEvent *event) {
  // 迷宫的最大长度或宽度为500个像素
  Q_UNUSED(event);
  paint = new QPainter;
  paint->begin(this);
  paint->setPen(QPen(Qt::black, 1, Qt::SolidLine));//设置画笔形式
  // 得到迷宫中每个方块的大小
  int max_size = (this->row > this->col) ? this->row : this->col;
  int each_box_size = 500 / max_size;
  for (int i = 0; i < this->row; i++) {
    for (int j = 0; j < this->col; j++) {
      // 重复对每个方块进行绘制
      if (this->maze_data[i][j] == 0) {
        // 如果是路则将画笔设为白色
        paint->setBrush(QBrush(Qt::white, Qt::SolidPattern));//设置画刷形式
      }else if(this->maze_data[i][j] == -1) {
        // 如果是墙路径则将画笔设为黄色
        paint->setBrush(QBrush(Qt::yellow, Qt::SolidPattern));
      }else if (this->maze_data[i][j] == 1) {
        // 如果是墙则将画笔设为黑色
        paint->setBrush(QBrush(Qt::black, Qt::SolidPattern));
      } else if (this->maze_data[i][j] == 2) {
        // 如果是起点则将画笔设为绿色
        paint->setBrush(QBrush(Qt::green, Qt::SolidPattern));
      } else if (this->maze_data[i][j] == 3) {
        // 如果是终点则将画笔设为红色
        paint->setBrush(QBrush(Qt::red, Qt::SolidPattern));
      }
      paint->drawRect(240 + each_box_size * i, 70 + each_box_size * j, each_box_size, each_box_size);
    }
  }
  paint->end();
}

在其他地方只需调用 repaint() 函数即可重新绘制迷宫

2，如何手动创建迷宫

获取鼠标每次点击时的位置并判断点击到第几个迷宫的方块，然后改变该方块的状态并保存到 maze_record 中

void MyWidget::mousePressEvent(QMouseEvent *event) {
  // 获取鼠标相对迷宫左上角的坐标
  int x = event->x() - 240;
  int y = event->y() - 70;
  if (x < 0 || y < 0 || this->maze_data == nullptr) {
    // 如果x，y小于0则直接跳出
    return;
  }
  // 得到迷宫中每个方块的大小
  int max_size = (this->row > this->col) ? this->row : this->col;
  int each_box_size = 500 / max_size;
  // 计算出鼠标点击的方块位置
  int click_row = x / each_box_size;
  int click_col = y / each_box_size;
  // 改变方块当前状态
  if (this->maze_record[click_row][click_col] == 0) {
    // 如果是路则变为墙
    this->maze_record[click_row][click_col] = 1;
  }else if (this->maze_record[click_row][click_col] == 1) {
    // 如果是墙则变为起点
    this->maze_record[click_row][click_col] = 2;
    if (this->start != nullptr) {
      // 如果已经有起点
      this->maze_record[this->start->x][this->start->y] = 0;
      this->start->x = click_row;
      this->start->y = click_col;
    }else {
      // 如果未设置起点则设为起点
      this->start = nullptr;
      this->start = new Point(click_row, click_col, 2);
    }
  }else if (this->maze_record[click_row][click_col] == 2) {
    // 如果是起点，则设置为终点
    delete this->start;
    this->start = nullptr;
    this->maze_record[click_row][click_col] = 3;
    if (this->end != nullptr) {
      // 如果终点已经存在
      this->maze_record[this->end->x][this->end->y] = 0;
      this->end->x = click_row;
      this->end->y = click_col;
    }else {
      this->end = new Point(click_row, click_col, 3);
    }
  }else if (this->maze_record[click_row][click_col] == 3) {
    // 如果是终点，则设置为路
    delete this->end;
    this->end = nullptr;
    this->maze_record[click_row][click_col] = 0;
  }
  this->resetMazeData();  // 就是把maze_record拷贝给maze_data
  this->repaint();

如果鼠标点击的位置在迷宫外面就直接退出该函数了，对其他操作没有影响

3，如何自动创建迷宫

参考自然分岔型^[1:1]，思路说的很清楚，我感觉自己代码写的好乱。。。不建议参考

int **MyWidget::autoSetMaze(int row, int col) {
  QList<Point*> path_list;
  int ** res = new int * [row];
  for (int i = 0; i < row; i++) {
    res[i] = new int[col];
  }
  for (int i = 0; i < row; i++) {
    int flag = i % 2;
    for (int j = 0; j < col; j++) {
      if (flag == 0) {
        // 单数行全为墙
        res[i][j] = 1;
      }else {
        // 偶数行墙和路依次分布
        if (j % 2 == 0) {
          res[i][j] = 1;
        }else {
          res[i][j] = 0;
        }
      }
    }
  }
  // 随机选取地图边缘的路
  int flag_xy = randomNumber(0, 10);
  int x = 0;
  int y = 0;
  if (flag_xy % 2 == 0) {
    x = 1;
    y = 2 * randomNumber(0, (col - 1) / 2) + 1;
  } else {
    y = 1;
    x = 2 * randomNumber(0, (row - 1) / 2) + 1;
  }
  // 将该点做标记
  res[x][y] = 10;
  // 将该点周围的墙加入数组中
  if (x != 1 && res[x - 1][y] != 10) {
    path_list.push_back(new Point(x - 1, y, 0));
  }
  if (x != row - 2 && res[x + 1][y] != 10) {
    path_list.push_back(new Point(x + 1, y, 0));
  }
  if (y != 1 && res[x][y - 1] != 10) {
    path_list.push_back(new Point(x, y - 1, 0));
  }
  if (y != col - 2 && res[x][y + 1] != 10) {
    path_list.push_back(new Point(x, y + 1, 0));
  }
  while (path_list.empty() == false) {
    // 数组中随机选取一个点
    int index = randomNumber(0, path_list.size());
    Point * ptr = path_list[index];
    int ptr_x = ptr->x;
    int ptr_y = ptr->y;
    // 从左到右
    if (res[ptr_x - 1][ptr_y] == 10 && res[ptr_x + 1][ptr_y] == 0) {
      res[ptr_x][ptr_y] = 10;
      res[ptr_x + 1][ptr_y] = 10;
      // 将周围的墙加入数组中
      if (ptr_x + 1 != row - 2 && res[ptr_x + 3][ptr_y] != 10) {
        path_list.push_back(new Point(ptr_x + 2, ptr_y, 0));
      }
      if (ptr_y != 1 && res[ptr_x + 1][ptr_y - 2] != 10) {
        path_list.push_back(new Point(ptr_x + 1, ptr_y - 1, 0));
      }
      if (ptr_y != col - 2 && res[ptr_x + 1][ptr_y + 2] != 10) {
        path_list.push_back(new Point(ptr_x + 1, ptr_y + 1, 0));
      }
    }
    // 从右到左
    if (res[ptr_x + 1][ptr_y] == 10 && res[ptr_x - 1][ptr_y] == 0) {
      res[ptr_x][ptr_y] = 10;
      res[ptr_x - 1][ptr_y] = 10;
      // 将周围的墙加入数组中
      if (ptr_x - 1 != 1 && res[ptr_x - 3][ptr_y] != 10) {
        path_list.push_back(new Point(ptr_x - 2, ptr_y, 0));
      }
      if (ptr_y != 1 && res[ptr_x - 1][ptr_y - 2] != 10) {
        path_list.push_back(new Point(ptr_x - 1, ptr_y - 1, 0));
      }
      if (ptr_y != col - 2 && res[ptr_x - 1][ptr_y + 2] != 10) {
        path_list.push_back(new Point(ptr_x - 1, ptr_y + 1, 0));
      }
    }
    // 从上到下
    if (res[ptr_x][ptr_y - 1] == 10 && res[ptr_x][ptr_y + 1] == 0) {
      res[ptr_x][ptr_y] = 10;
      res[ptr_x][ptr_y + 1] = 10;
      // 将周围的墙加入数组中
      if (ptr_x != row - 2 && res[ptr_x + 2][ptr_y + 1] != 10) {
        path_list.push_back(new Point(ptr_x + 1, ptr_y + 1, 0));
      }
      if (ptr_x != 1 && res[ptr_x - 2][ptr_y + 1] != 10) {
        path_list.push_back(new Point(ptr_x - 1, ptr_y + 1, 0));
      }
      if (ptr_y + 1!= col - 2 && res[ptr_x][ptr_y + 3] != 10) {
        path_list.push_back(new Point(ptr_x, ptr_y + 2, 0));
      }
    }
    // 从下到上
    if (res[ptr_x][ptr_y + 1] == 10 && res[ptr_x][ptr_y - 1] == 0) {
      res[ptr_x][ptr_y] = 10;
      res[ptr_x][ptr_y - 1] = 10;
      // 将周围的墙加入数组中
      if (ptr_x != row - 2 && res[ptr_x + 2][ptr_y - 1] != 10) {
        path_list.push_back(new Point(ptr_x + 1, ptr_y - 1, 0));
      }
      if (ptr_x != 1 && res[ptr_x - 2][ptr_y - 1] != 10) {
        path_list.push_back(new Point(ptr_x - 1, ptr_y - 1, 0));
      }
      if (ptr_y - 1 != 1 && res[ptr_x][ptr_y - 3] != 10) {
        path_list.push_back(new Point(ptr_x, ptr_y - 2, 0));
      }
    }
    path_list.removeAt(index);
  }
  for (int i = 0; i < row; i++) {
    for (int j = 0; j < col; j++) {
      if (res[i][j] == 10) {
        res[i][j] = 0;
      }
    }
  }
  // 随机选取一些墙将其变为路，方法随意，这里仅供参考
  if (col > 20 || row > 20) {
    for (int i = 0; i < row * 5; i++) {
      int x = randomNumber(0, 100) % (row - 2) + 1;
      int y = randomNumber(0, 100) % (col - 2) + 1;
      if (res[x][y] == 1) {
        // 这里是要判断这面墙的上下左右至少有2面都为墙
        int flag = 0;
        if (res[x - 1][y] == 1) {
          flag++;
        }
        if (res[x + 1][y] == 1) {
          flag++;
        }
        if (res[x][y - 1] == 1) {
          flag++;
        }
        if (res[x][y + 1] == 1) {
          flag++;
        }
        if (flag > 1) {
          res[x][y] = 0;
        }
      }
    }
  }
  return res;
}

因为单纯使用自然分岔的方法产生的迷宫的通路很少，所以在行数或列数大于 20 的时候随机选取一些墙将其变为路，这样一个迷宫可以有好多条路可以走。

4，关于 BFS 寻路的细节

DFS 寻路的路径直接保存到栈中，所以路径可以直接得出；而 BFS 寻路使用的是队列，无法直接保存路径，所以我自定义了队列 MyQueue，使用线性结构，在 Point 类中添加 pioneer 属性，其值是该点在 MyQueue 中后继的点，最后寻路时直接通过不断访问 MyQueue[Point.pioneer] 就可以得到整个路径

class Point {
 public:
  Point();
  Point(int x, int y, int stat);

  bool operator!=(const Point & p);
 public:
  int x;
  int y;
  int status;
  int pioneer;
};

class MyQueue {
 public:
  MyQueue();
  bool isEmpty();
  void push(Point * p);
  void pop();
  Point* frontPoint();
  Point ** queue;
  int front;
  int end;
};

5，寻路动画的实现

不管使用 BFS 或 DFS 寻路时最后都会用到栈，将通路节点依次出栈的同时将 maze_data 相应位置变为 -1，然后进行 repaint() 并延时 0.1s

这里给出我使用的延时函数

void MyWidget::sleep(int sec) {
  QElapsedTimer t;
  t.start();
  while(t.elapsed()<sec);
}

五，其他

这次的程序写了好久。。。主要是不知道怎么使用Qt。

还有一种思路其实更节省空间，每走一步将maze_data该处的值减去已走过的步数，如[2,0,0,0,0,0,3]走完就变成[2,-1,-2,-3,-4,-5,3]，直到无路可走时直接原路返回，如果某处相邻点值为0，则走到该点处，并将该点数值设为已走过的步数，最后寻路时优先选择相邻位置差值最大的点。

自然分岔型：三套简单的迷宫地图生成方案 - 兔四的文章 - 知乎，这里介绍了几种自动生成迷宫的方法 ↩︎ ↩︎

posted @ 2020-12-18 20:24 Mezzベ阅读(651) 评论(0) 收藏举报

刷新页面返回顶部