JAVA做题笔记——方法
第1题
【描述】
正多边形是一个有n条边的多边形,每条边的长度side相同,每个角的度数也相同。求正多边形面积的公式如下:
计算机生成了可选文字:
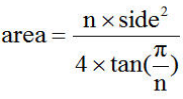
定义方法:public static double area(int n, double side),该方法返回正多边形面积。
编写一个main方法,输入正多边形的边数和边长,调用area方法,显示它的面积。
【输入】
第一行一个正整数,表示正多边形的边数。
第二行一个实数,表示正多边形的边长。
【输出】
一行中输出对应的正多边形面积,结果保留2位小数。
【输入示例】
5
3
【输出示例】
15.48
【提示】
需使用 Main 作为主类名。
代码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
double side = in.nextDouble();
System.out.printf("%.2f\n", area(n, side));
in.close();
}
// 请在此处编写area方法
public static double area(int n, double side) {
double Area =(n*Math.pow(side, 2))/(4*Math.tan(Math.PI/n));
return Area;
}
}
第2题
【描述】
求一个整数各位数字之和。定义方法:public static int sumDigits(int n),该方法返回一个整数各位数字之和。
编写一个main方法,输入一个整数,调用sumDigits方法,显示该整数各位数字之和。
【输入】
一行中给出一个整数。
【输出】
一行中输出该整数各位数字之和。
【输入示例】
3456
【输出示例】
18
【提示】
需使用 Main 作为主类名。
代码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int value = in.nextInt();
System.out.println(sumDigits(value));
in.close();
}
// 请在此处编写sumDigits方法
public static int sumDigits(int n) {
int add=0;
while(true) {
if(n/10==0) {
add+=n;
break;
}//确认数字是不是一位数
else {
add+=n%10;
n/=10;
}
}
return add;
}
}
第3题
【描述】
求一个整数的逆序数。定义方法:public static int reverse(int n),该方法返回一个整数的逆序数。
编写一个main方法,输入一个整数,调用reverse方法,显示该整数的逆序数。
【输入】
一行中给出一个整数。
【输出】
一行中输出该整数的逆序数。
【输入示例】
-123
【输出示例】
-321
【提示】
需使用 Main 作为主类名。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
System.out.println(reverse(n));
in.close();
}
// 请在此处编写reverse方法
public static int reverse(int n) {
int sum, result;
if(n<0){
System.out.print("-");
n = n * -1;
}
sum = 0;
while(n!=0){
result = n % 10;
sum = sum * 10 + result;
n = n / 10;
}
return sum;
}
第4题
【描述】
输入一个整数,判断它是否是回文整数。如果一个整数的逆序数和原数一样,这个整数就称为回文整数
定义方法:public static boolean isPalindrome(int n),如果n是回文数,返回true,否则返回false。
编写一个main方法,输入一个整数,调用isPalindrome方法,判断该整数是否为回文整数。如果该整数是回文数,输出true,否则输出false。
【输入】
一行中给出一个整数。
【输出】
如果该整数是回文数,输出true,否则输出false。
【输入示例】
616
【输出示例】
true
【提示】
需使用 Main 作为主类名。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
System.out.println(isPalindrome(n));
in.close();
}
// 请在此处编写isPalindrome函数
public static boolean isPalindrome(int n) {
int sum=0;
if(n<0 || (n/10!=0 && n%10==0))
{
return false;
}
else{
while(n>sum)
{
sum = sum * 10 + n%10;
n = n/10;
}
}
/*若整数为偶数*/
if(sum == n)
{
return true;
}
/*若整数位数为奇数*/
if(sum/10 == n)
{
return true;
}
return false;
}
}
第5题
【描述】
分数可以表示为“分子/分母”的形式。编写程序,输入一个分数,然后将其约分为最简分式。最简分式是指分子和分母不具有可以约分的成分了。如6/12可以被约分为1/2。当分子大于分母时,不需要表达为整数又分数的形式,即11/8还是11/8;而当分子分母相等时,仍然表达为1/1的分数形式。
定义方法:public static int gcd(int m, int n),返回m和n的最大公约数。
编写一个main方法,输入一个分数,调用gcd方法,将该分数约分为最简分式并输出。
【输入】
在一行中给出一个分数,分子和分母中间以斜杠“/”分隔,如:12/34。分子和分母都是正整数(不包含0)。
【输出】
在一行中输出这个分数对应的最简分式,格式与输入相同,如 6/17。
【输入示例】
60/120
【输出示例】
1/2
【提示】
需使用 Main 作为主类名。
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner in = new Scanner(System.in);
String num = in.nextLine();
int n = num.indexOf('/');
int a = Integer.parseInt(num.substring(0, n));
int b = Integer.parseInt(num.substring(n+1));
System.out.println(a/gcd(a,b)+"/"+b/gcd(a,b));
in.close();
}
public static int gcd(int m, int n) {
if(m==1||n==1)
return 1;
int gcd=0;
int k=2;
while(k<=m&&k<=n) {
if(m%k==0&&n%k==0)
gcd=k;
k++;
}
if (gcd==0)
return 1;
else return gcd;
}
}
}
第6题
【描述】
编写程序,输出前n(n≤100)个回文素数,每行显示5个,并适当对齐。回文素数是这样一种素数:本身为素数且也是回文数。例如,131是素数,也是回文数。
定义方法:public static boolean isPrime(int n),判断n是否是素数,如果是素数,返回true,否则返回false。
定义方法:public static boolean isPalindrome(intn),判断n是否是回文数,如果n是回文数,返回true,否则返回false。
编写一个main方法,输入一个正整数n,调用isPrime和isPalindrome方法,输出前n个回文素数。
【输入】
一行中给出一个正整数n。
【输出】
输出前n个回文素数,每行显示5个,每个宽度为6。
【输入示例】
10
【输出示例】
2 3 5 7 11
101 131 151 181 191
【提示】
对于整数i,如果isPrime(i)与isPalindrome(i)的返回值都是true,i即为回文素数。
需使用 Main 作为主类名。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
for(int i = 2, count = 0; count < n; ++i) {
if(isPrime(i) && isPalindrome(i)) {
System.out.printf("%6d", i);
++count;
if(count % 5 == 0)
System.out.println();
}
}
in.close();
}
// 请在此处分别编写isPrime方法和isPalindrome方法
public static boolean isPrime(int n) {
int k=2;
if(n<k)return false;
else if(n==k)return true;
while(k<n) {
if(n%k==0)return false;
k++;
}
return true;
}
public static boolean isPalindrome(int n) {
if(n/10==0)return true;
String nstr=n+"";
int leng = nstr.length();//str.equals(str1)
if(leng%2==0&&(nstr.substring(leng/2)).equals(nstr.substring(0,leng/2)))
return true;
else if(leng%2!=0&&(nstr.substring((leng/2)+1).equals(nstr.substring(0,leng/2))))
return true;
return false;
}
}
第7题
【描述】
一个正整数的因子是所有可以整除它的正整数。而一个数如果恰好等于除它本身外的因子之和,这个数就称为完数。例如6是完数,6=1+2+3(6的因子是1、2、3)。
定义方法:public static boolean isPerfectNumber(int n),判断n是否是素数完数,如果是完数,返回true,否则返回false。
编写一个main方法,读入两个正整数n和m(1≤n<m<1000),输出[n, m]范围内所有的完数。
【输入】
一行中给出两个正整数,其间以空格分隔。
【输出】
输出[n, m]范围内所有的完数,其间以空格分隔,最后一个数字后面没有空格。如果没有完数,则输出一个空行。
【输入示例】
1 10
【输出示例】
6
【提示】
需使用 Main 作为主类名。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
boolean flag = true;
for(int i = n; i <= m; ++i) {
if(isPerfectNumber(i)) {
if(flag) {
System.out.printf("%d", i);
flag = false;
}
else
System.out.printf(" %d", i);
}
}
System.out.printf("\n");
in.close();
}
// 请在此处编写isPerfectNumber方法
public static boolean isPerfectNumber(int n) {
int sum=0;
for(int i=1;i<=n/2;i++)
if(n%i==0)sum+=i;
return sum==n?true:false;
}
}
第8题
【描述】
定义和调用如下计算面积的方法:
public static double computeArea(double radius = 1);
public static double computeArea(double width, double height);
public static public double computeArea(double side1, double side2, double side3);
分别计算圆、矩形和三角形的面积。如果函数返回的面积为0,表示输入数据不合法。π值为3.14159。要求用方法重载实现。
isValid方法用于判断三角形合法性:
static bool isValid(double side1, double side2, double side3);
【输入】
输入有三行:第一行圆半径;第二行矩形宽度和高度,两个实数以空格间隔;第三行三角形边长,三个实数以空格间隔。
【输出】
分行输出对应的圆、矩形和三角形面积。
【输入示例】
5
10 10
1 2 3
【输出示例】
78.53975
100.0
0.0
【提示】
需使用 Main 作为主类名。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
double radius = in.nextDouble();
double width = in.nextDouble();
double height = in.nextDouble();
double side1 = in.nextDouble();
double side2 = in.nextDouble();
double side3 = in.nextDouble();
System.out.println(computeArea(radius));
System.out.println(computeArea(width, height));
System.out.println(computeArea(side1, side2, side3));
}
// 请在此处分别编写computeArea方法和isValid方法
public static double computeArea(double radius) {
final double PI=3.14159;
return PI*radius*radius;
}
public static double computeArea(double width, double height){
return width*height;
}
public static double computeArea(double side1, double side2, double side3) {
if(isValid(side1, side2, side3)!=true)
return 0.0;
double p = (side1+side2+side3)*0.5;
double s = Math.sqrt(p*(p-side1)*(p-side2)*(p-side3));
return s;
}
static boolean isValid(double side1, double side2, double side3){
if(side1==0||side2==0||side3==0)return false;
if(side1+side2>side3&&side3+side2>side1&&side3+side1>side2)
return true;
else return false;
}
}
第9题
【描述】
定义方法:public static double squareRoot(double value),返回value的平方根。
编写一个main方法,读入一个数,调用squareRoot方法,输出该数的平方根。
可以通过对下面公式的反复计算近似地得到平方根:
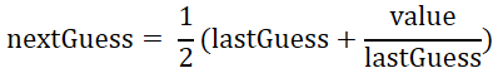
当nextGuess和lastGuess几乎相同时,nextGuess就是平方根的近似值。nextGuess最初的猜测值可以是任意一个值(例如1.0)。这个值就是lastGuess的初始值。如果nextGuess和lastGuess的差小于一个很小的数(例如0.000001),就可以认为nextGuess是value平方根的近似值;否则,nextGuess就赋值给lastGuess,迭代过程继续进行。
【输入】
一行中给出一个数。
【输出】
输出该数的平方根。
【输入示例】
2
【输出示例】
1.414214
【提示】
注意:不能使用数学类Math中的sqrt方法。
需使用 Main 作为主类名。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
double value = in.nextDouble();
System.out.printf("%f\n", squareRoot(value));
in.close();
}
// 请在此处编写squareRoot方法
public static double squareRoot(double value){
double nextGuess = value, lastGuess = 1;
while(Math.abs(nextGuess-lastGuess) >= 0.00001)
{
lastGuess = nextGuess;
nextGuess = (lastGuess + value / lastGuess) / 2;
}
return nextGuess;
}
}
第10题
【描述】
信用卡号遵循下面的模式:
一个信用卡号必须是13到16位的整数,它的开头必须是4(指Visa卡)或5(指Master卡)或37(指American Express卡)或6(指Discover卡)。
在1954年,IBM的Hans Luhn提出了一种算法,该算法可以验证信用卡号的有效性。这个算法在确定输入的卡号是否正确,或者信用卡是否被扫描仪正确扫描方面是非常有用的。遵循这个算法,可以生成所有的信用卡号。通常称为Luhn检测或者Mod10检测,可以描述如下(假设卡号为4388576018402626):
(1)从右到左对偶数位的数字进行翻倍,如果某个数字翻倍后的结果是一个两位数,那么就将这个两位数的个位和十位相加得到一个一位数。
2×2=4,2×2=4,4×2=8,2×2=4,1×2=2,6×2=12(1+2=3),5×2=10(1+0=1),8×2=16(1+6=7),4×2=8
(2)将(1)中得到的所有一位数相加。
4+4+8+2+3+1+7+8=37
(3)从右到左对奇数位的数字进行相加。
6+6+0+8+0+7+8+3=38
(4)将(2)和(3)中得到的结果相加。
37+38=75
(5)如果(4)中得到的结果能被10整除,那么卡号是合法的,否则卡号是不合法的。
定义方法:public static int getSize(long n),返回信用卡号n的位数。
定义方法:public static int getDigit(int n),若n是一位数,直接返回n;若n是两位数,将这个两位数的个位和十位相加得到一个一位数并返回。
定义方法:public static int sumOfDoubleEvenPlace(long n),返回信用卡号从右到左偶数位的数字翻倍后的和。
定义方法:public static int sumOfOddPlace(long n),返回信用卡号从右到左奇数位的数字和。
定义方法:publicstatic boolean isValid(long n),调用sumOfDoubleEvenPlace和sumOfOddPlace方法,判断n是否为合法的信用卡号,如果是合法的,返回true,否则返回False。
编写一个main方法,输入一个信用卡号,调用isValid方法,如果信用卡号是合法的,输出true,否则输出false。
【输入】
一行中给出一个信用卡号(长整型)。
【输出】
如果信用卡号是合法的,输出true,否则输出false。
【输入示例】
4388576018402626
【输出示例】
false
【提示】
需使用 Main 作为主类名。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
long cardNumber = in.nextLong();
System.out.println(isValid(cardNumber));
in.close();
}
public static int getSize(long n) {
String srt =n+"";
return srt.length();
}
public static int getDigit(int n) {
if(n<10)
return n;
else
return n/10+n%10;
}
public static int sumOfDoubleEvenPlace(long n) {
int sum=0;
long p =n;
for(int i=1;i<=getSize(n);i++) {
if(i%2==0)
sum+=getDigit((int)(p%10)*2);
p/=10;
}
return sum;
}
public static int sumOfOddPlace(long n) {
int sum=0;
long p =n;
for(int i=1;i<=getSize(n);i++) {
if(i%2!=0)
sum+=p%10;
p/=10;
}
return sum;
}
public static boolean isValid(long n) {
return ((sumOfDoubleEvenPlace(n)+sumOfOddPlace(n))%10==0)?true:false;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号