基于Wiener退化模型的激光器件Laser数据集分析及EM算法等
目录:
一、题目
此为2024年浙江大学可靠性工程与维护管理课程大作业Project3部分解答。
本文不保证正确性(甚至不保证是否正确理解题意),且仅代表笔者观点。几乎所有的推导过程均借鉴他人论文,仅代码为笔者所写。故此文可能出现推导、定义等错误,且不同题目之间变量定义可能有差别(已经做了一定的统一)。
(以下题目为机翻)
1.1 背景和数据集
随着时间的推移,一些激光器件的光输出会因退化而降低。然而,电信系统中使用的激光器配备了反馈机制,该机制可以调整工作电流,以便在激光器退化时保持几乎恒定的光输出。当工作电流达到临界水平时,认为激光器出现故障。
激光设备的关键质量特征是其工作电流。当工作电流超过预定义的阈值(表示为 D = 10)时,认为激光器出现故障。电流每 250 小时测量一次,实验总持续时间为 4000 小时。在此期间收集的数据如图 1 所示,相关的数据文件名为 GaAsLaser.csv。
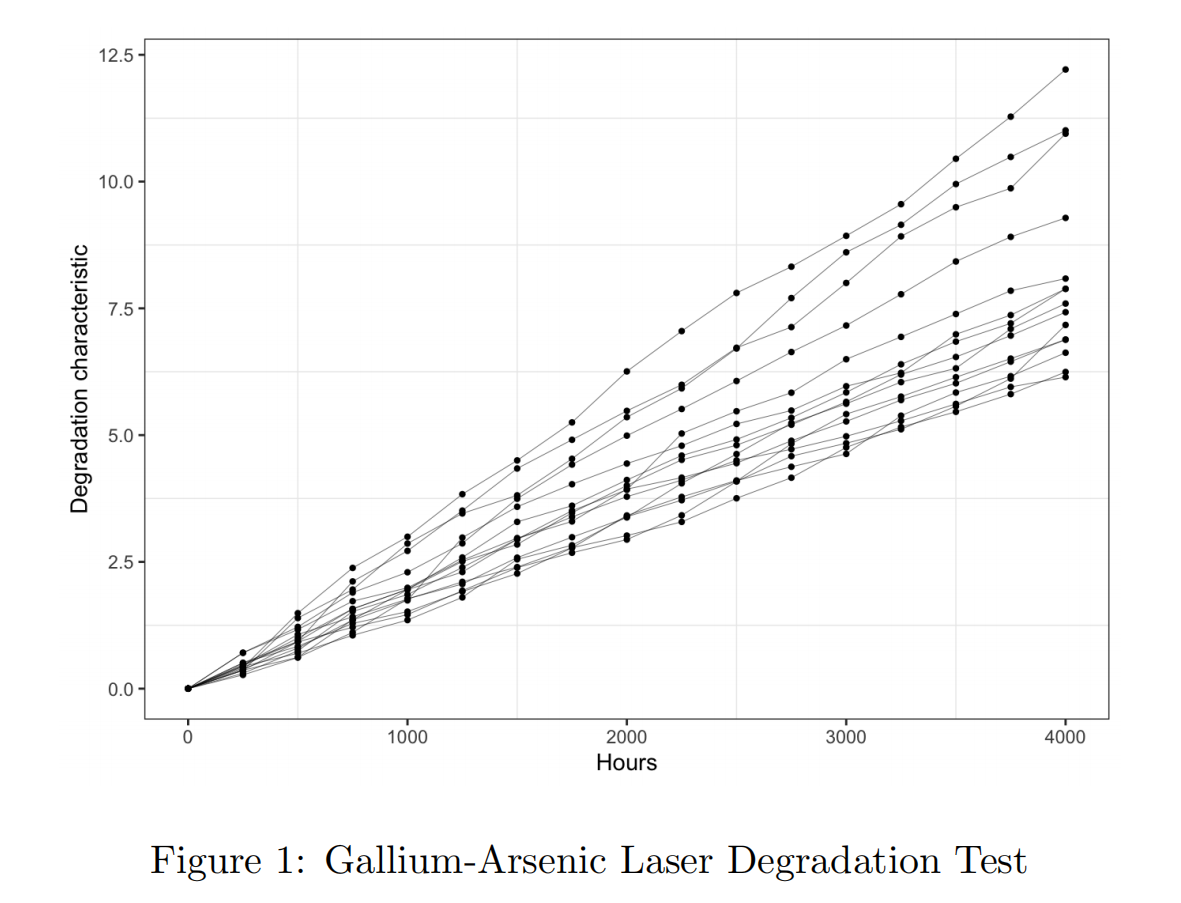
使用提供的数据,完成以下任务并提交一份全面的分析报告(包括背景、方法、计算步骤、结果讨论和代码实现)
1.2 任务
我们假设可以使用 Wiener 过程对降解数据进行建模,由以下模型表示:
其中\(\beta\)是漂移参数,\(\sigma\)是漫反射参数, \(\mathcal{B} (t)\)是法向布朗运动。根据维纳工艺的特性,回答以下问题:
- 根据实验数据(每 250 小时测量一次),估计漂移参数\(\mu\)和扩散参数\(\sigma\),并解释估计结果。
- 器件生命周期的累积分布函数是什么?尝试推导失效时间的分布函数 \(T_f=\inf\{t:X(t)\ge D\}\)。(What is the cumulative distribution function of the device’s lifetime? Try to derive the distribution function of the failure time \(T_f=\inf\{t:X(t)\ge D\}\))
- 继续(1)和(2),为派生的参数和分布函数推导出相应的 95% 置信区间(您可以使用 bootstrap、枢轴数量法、Wald 置信区间等)
- 为了解释器件之间的异质性,我们将参数\(\beta\)建模为遵循 \(\beta\sim N(\mu, \tau^2)\)正态分布。原始模型变为 \(M1\):
尝试使用期望最大化(EM)算法来估计参数\(\theta=(\mu,\tau,\sigma)\)和可靠性函数\(R(t)\)
1.3 输入格式(GaAsLaser.csv)
文件GaAsLaser.csv的格式如下(这里只展示了部分数据):
| Percent Increase | Unit Number | Hours |
|---|---|---|
| 0 | 101 | 0 |
| 0.4741 | 101 | 250 |
| 0.9255 | 101 | 500 |
| 2.1147 | 101 | 750 |
| 2.7168 | 101 | 1000 |
| 3.511 | 101 | 1250 |
| 4.3415 | 101 | 1500 |
| 4.9076 | 101 | 1750 |
| 5.4782 | 101 | 2000 |
| 5.9925 | 101 | 2250 |
| 6.7224 | 101 | 2500 |
| 7.1303 | 101 | 2750 |
| 8.0006 | 101 | 3000 |
| 8.9193 | 101 | 3250 |
| 9.494 | 101 | 3500 |
| 9.8675 | 101 | 3750 |
| 10.9446 | 101 | 4000 |
| 0 | 102 | 0 |
| 0.7078 | 102 | 250 |
| 1.2175 | 102 | 500 |
| 1.8955 | 102 | 750 |
| 2.2954 | 102 | 1000 |
| 2.865 | 102 | 1250 |
| 3.7454 | 102 | 1500 |
| 4.4192 | 102 | 1750 |
| 4.9894 | 102 | 2000 |
| 5.5148 | 102 | 2250 |
| 6.0668 | 102 | 2500 |
| 6.6385 | 102 | 2750 |
| 7.1615 | 102 | 3000 |
| 7.7778 | 102 | 3250 |
| 8.4242 | 102 | 3500 |
| 8.9092 | 102 | 3750 |
| 9.2834 | 102 | 4000 |
| \(\dots\) | \(\dots\) | \(\dots\) |
其中Percent Increase为退化数据,Unit Number为样本编号,Hours为观测时间。
二、部分解题
2.0 Wiener退化过程
称 \(\{X(t), t \geq 0\}\) 是漂移参数为 \(\mu\)、扩散参数为 \(\sigma\) 的(一元)Wiener过程,若:
- \(X(0) = 0\)
- \(\{X(t), t \geq 0\}\) 有平稳独立增量
- \(X(t)\) 服从均值为 \(\mu t\),方差为 \(\sigma^2 t\) 的正态分布
根据上面的定义, 可以将带漂移的 Wiener 过程表示为下面的形式:
式中:\(\{\mathcal{B}(t)\}, t \geq 0\) 是标准 Wiener 过程或标准布朗运动过程。
根据定义,对带漂移的 Wiener 过程,显然有如下的性质成立:
- 时刻 \(t \sim t + \Delta t\) 之间的增量服从正态分布,即 \(\Delta X = X(t + \Delta t) - X(t) \sim \mathcal{N}(\mu \Delta t, \sigma^2 \Delta t)\)。
- 对任意两个不相交的时间区间 \([t_1, t_2], [t_3, t_4]\),其中 \(t_1 < t_2 \leq t_3 < t_4\),增量 \(X(t_4) - X(t_3)\) 与 \(X(t_2) - X(t_1)\) 相互独立。
2.1 估计漂移参数\(\mu\)和扩散参数\(\sigma\)
2.1.1 建模计算分析
由 Wiener 过程的性质, 容易知道
于是由退化数据 \(X_{ij},(i = 1, 2, \cdots, n; \ j = 1, 2, \cdots, m_i)\),得到模型参数的似然函数为
对式(1.1)求偏导,可以求得漂移参数 \(\mu\) 和扩散参数 \(\sigma^2\) 的极大似然估计如下:
通过MATLAB代码获得结果为\(\mu=0.002037906666667\),\(\sigma=0.012281685807089\)。
2.1.2 代码部分
2.1.2.1 代码实现
Laser_dat = readtable('GaAsLaser.csv');
N = 15;
M = 17;
format long;
x = zeros(N, M); % x: Percent Increase
t = zeros(N, M); % t: Hours
for i = 1 : N
for j = 1 : M
x(i, j) = Laser_dat.PercentIncrease((i - 1) * M + j);
t(i, j) = Laser_dat.Hours((i - 1) * M + j);
end
end
SXm = 0; Stm = 0; % \sum{X_{im}}, \sum{t_{im}}
SSX2dt = 0; % \sum_i\sum_j{\dfrac{(\Delta Y_{ij})^2}{\Delta t_{ij}}}
for i = 1 : N
for j = 1 : M - 1
SSX2dt = SSX2dt + (x(i, j + 1) - x(i, j))^2 / (t(i, j + 1) - t(i, j));
end
SXm = SXm + x(i, M);
Stm = Stm + t(i, M);
end
mu = SXm / Stm
sigma = sqrt((SSX2dt - SXm ^ 2 / Stm) / N / M)
2.1.2.2 输出
\(\mu=0.002037906666667\)
\(\sigma=0.012281685807089\)
2.2 计算\(F_T\)与\(f_t\)
以下借鉴了金光.基于退化的可靠性技术——模型、方法及应用[M].国防工业出版社,2014.
在一元 Wiener 过程 \(\{X(t), t \geq 0\}\) 的基础上,定义随机过程 \(\{Z(t), t \geq 0\}\) 为:
即任意时刻\(t\ge 0\),\(Z(t)\) 取 \(X(t)\)在时间 \([0,t]\)内的最大值。
记时刻 $ t $ 时 $ Z(t) $ 的概率密度函数为 $ g(z,t) $,由 $ {Z(t), t \geq 0 } $ 的定义可知其是单调随机过程。则产品在时间 $ t $ 内不失效的概率为
因而只需要求出 \(g(z,t)\) 即可得到寿命 \(T\) 的分布。利用 Fokker-Planck 方程可以得到 \(g(z,t)\) 的形式为
将式(2.2)带入式(2.1)可得到
进一步得到 \(T\) 的分布函数和概率密度函数分别为
式中,\(\Phi(\cdot)\)表示标准正态分布的CDF。
2.3 推导95%置信区间
2.3.1 分析计算
采用bootstrap方法,对数据集中的\(15\)组数据进行放回的采样,每次取可重复的\(15\)组数据,计算它们的\(\mu\),\(\sigma\)以及累积分布函数\(F_T(t)\)(CDF)(式(2.4))、概率密度函数\(f_T(t)\)(PDF)(式(2.5)),取的次数足够多的情况下,对取得的数据进行排列,选取其中\(95\%\)的数据即为\(95\%\)置信区间。
2.3.2 代码部分
2.3.2.1 分析
正态累积分布函数表示为
注意到MATLAB中并没有现成的\(\Phi(x)\),但存在误差函数\(\mathrm{erf}(x)\)
故有
2.3.2.2 代码实现
Laser_dat = readtable('GaAsLaser.csv');
rng(0);
N = 15;
M = 17;
MM = 401; % 概率密度函数观察次数
CNT = 5000; % 有放回的抽样次数
alpha = 0.95; % 置信度
L = round(CNT * (1 - alpha) / 2); R = CNT - L; % 置信区间上下界
D = 10; % 失效阈值
Tim = linspace(2000, 8000, MM); % 观测时间点
format long;
x = zeros(N, M); % x: Percent Increase
t = zeros(N, M); % t: Hours
for i = 1 : N
for j = 1 : M
x(i, j) = Laser_dat.PercentIncrease((i - 1) * M + j);
t(i, j) = Laser_dat.Hours((i - 1) * M + j);
end
end
qmu = zeros(1, CNT); % mu的队列
qsigma = zeros(1, CNT); % sigma的队列
num = zeros(1, N); % 每次选取的数据编号
f = zeros(CNT, MM); % 每一次抽样的概率密度函数的每个观测点的值
F = zeros(CNT, MM); % 每一次抽样的累积分布函数的每个观测点的值
cnt = 0;
for T = 1 : CNT
cnt = cnt + 1;
num = randi([1, N], 1, N);
SXm = 0; Stm = 0; % \sum{X_{im}}, \sum{t_{im}}
SSX2dt = 0; % \sum_i\sum_j{\dfrac{(\Delta Y_{ij})^2}{\Delta t_{ij}}}
for i = 1 : N
for j = 1 : M - 1
SSX2dt = SSX2dt + (x(num(i), j + 1) - x(num(i), j))^2 / (t(num(i), j + 1) - t(num(i), j));
end
SXm = SXm + x(num(i), M);
Stm = Stm + t(num(i), M);
end
mu = SXm / Stm; sigma = sqrt((SSX2dt - SXm ^ 2 / Stm) / N / M);
qmu(cnt) = mu;
qsigma(cnt) = sigma;
for i = 1 : MM
ti = Tim(i);
f(cnt, i) = D / sqrt(2 * pi * sigma^2 * ti^3) * exp(-(D - mu * ti)^2 / (2 * sigma^2 * ti));
F(cnt, i) = phi((mu * ti - D) / (sigma * sqrt(ti))) + exp((2 * mu * D) / (sigma^2)) * phi(-(mu * ti + D) / (sigma * sqrt(ti)));
end
end
% 输出mu和sigma的95%置信区间
qmu = sort(qmu);
qsigma = sort(qsigma);
[qmu(L), qmu(R)]
[qsigma(L), qsigma(R)]
f = sort(f, 1);
fL = zeros(1, MM);
fM = zeros(1, MM);
fR = zeros(1, MM);
F = sort(F, 1);
FL = zeros(1, MM);
FM = zeros(1, MM);
FR = zeros(1, MM);
for i = 1 : MM
fL(i) = f(L, i);
fR(i) = f(R, i);
FL(i) = F(L, i);
FR(i) = F(R, i);
end
% 计算真实的mu,sigma和f(t),F(t)
SXm = 0; Stm = 0; % \sum{X_{im}}, \sum{t_{im}}
SSX2dt = 0; % \sum_i\sum_j{\dfrac{(\Delta Y_{ij})^2}{\Delta t_{ij}}}
for i = 1 : N
for j = 1 : M - 1
SSX2dt = SSX2dt + (x(i, j + 1) - x(i, j))^2 / (t(i, j + 1) - t(i, j));
end
SXm = SXm + x(i, M);
Stm = Stm + t(i, M);
end
mu = SXm / Stm; sigma = sqrt((SSX2dt - SXm ^ 2 / Stm) / N / M);
for i = 1 : MM
ti = Tim(i);
fM(i) = D / sqrt(2 * pi * sigma^2 * ti^3) * exp(-(D - mu * ti)^2 / (2 * sigma^2 * ti));
FM(i) = phi((mu * ti - D) / (sigma * sqrt(ti))) + exp((2 * mu * D) / (sigma^2)) * phi(-(mu * ti + D) / (sigma * sqrt(ti)));
end
figure;
subplot(1, 2, 1); % CDF
hold on;
plot(Tim, FM, 'Color', 'red', 'LineWidth', 1);
plot(Tim, FL, Tim, FR, 'Color', 'blue', 'LineWidth', 1, 'LineStyle', '--');
title('Estimated life time distribution and 95% pointwise confidence band for D = 10');
xlabel('Time(hour)');
ylabel('CDF');
legend('Point estimate', '95% Confidence band', 'Location', 'best');
hold off;
subplot(1, 2, 2); % PDF
hold on;
plot(Tim, fM, 'Color', 'red', 'LineWidth', 1);
plot(Tim, fL, Tim, fR, 'Color', 'blue', 'LineWidth', 1, 'LineStyle', '--');
title('The distribution function and 95% pointwise confidence band for D = 10');
xlabel('Time(hour)');
ylabel('PDF');
legend('Point estimate', '95% Confidence band', 'Location', 'best');
hold off;
function res = phi(x)
res = 1 / 2 * (1 - erf(-x / sqrt(2)));
end
2.3.2.3 输出
重复采样次数\(CNT=5000\)情况下,\(95\%\)置信区间分别为:
\(\mu:[0.001825663333333, 0.002271778333333]\)
\(\sigma:[0.009998109067984,0.013810250680994]\)
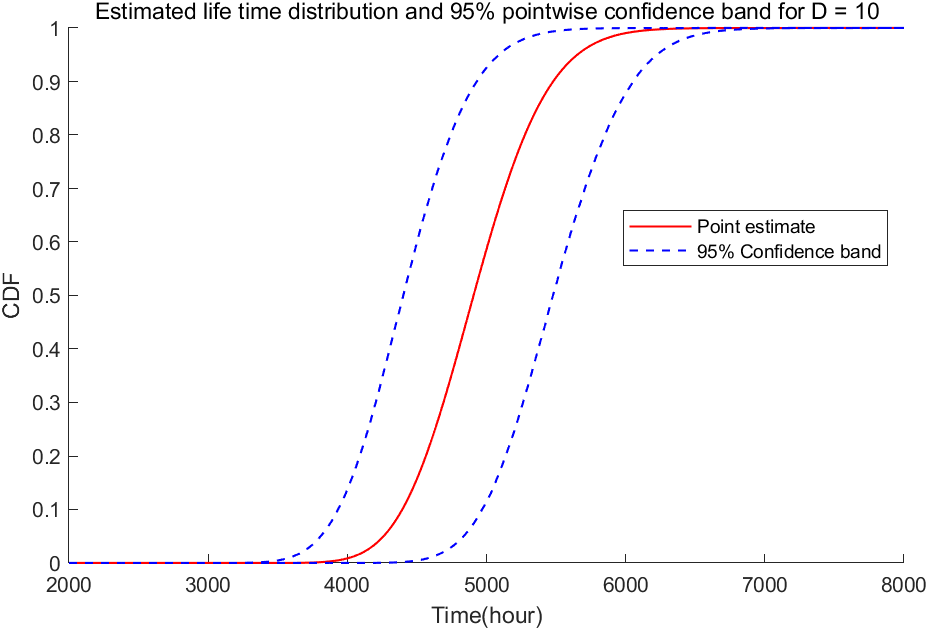

2.4 估计参数\(\theta=(\mu,\tau,\sigma)\)和可靠性函数\(R(t)\)
2.4.1 EM算法估计参数
以下借鉴了论文潘东辉.基于退化数据的产品可靠性建模与剩余寿命预测方法研究[D].华中科技大学,2014.
假设有 \(n\) 个样本参与退化试验,分别对每个单体 \(i\) 在一些离散的时间点 \(t_{ij}\) 进行监测,获得退化数据,即 \(X_{ij} = X(t_{ij}), (i = 1, \ldots, n;\ j = 0, 1, \ldots, m_i)\)。这类数据是具有单调趋势的函数型数据的一个特例。
为了后续叙述的方便,我们定义以下符号:
- \(\mathbf{X}\):对所有 \(n\) 个样本进行监测获得的退化数据集。
- \(\mathbf{X}_i\):对应于第 \(i\) 个单体的退化数据集,即 \(\mathbf{X}_i = (X_{i0}, X_{i1}, \ldots, X_{im_i})'\)。
- \(\mathbf{X}\) 的整体表示为 \(\mathbf{X} = (\mathbf{X}_1', \ldots, \mathbf{X}_n)'\)。
- 由于采用的数据集样本之间观测时间相同,即 \(t_{j} = t_{ij}, (i = 1, \ldots, n)\),以下的 \(t_j\) 与 \(t_{ij}\) 含义相同;同理,由于观测次数相同,即\(m = m_{i}, (i = 1, \ldots, n)\),以下的 \(m\) 与 \(m_{i}\) 含义相同。
设 \(\Delta X_{ij} = X_{ij} - X_{i(j-1)}\) 为第 \(i\) 个单体从时刻 \(t_{j-1}\) 到时刻 \(t_j\) 的退化增量。
目标是基于测量获得的退化数据 \(\mathbf{X}\) 来估计模型中的未知参数 \(\Theta = (\mu_\beta, \tau_\beta^2, \sigma^2)\)。其中,\(\beta_i\) 表示对应于单体 \(i\) 的漂移参数,并且令 \(\Omega = (\beta_1, \ldots, \beta_n)\)。
根据 Wiener 过程的性质,对于给定的 \(\beta_i\),对应于 \(\mathbf{X}_i\) 的抽样分布服从如下形式的多变量高斯分布
其中,\(\Delta t_j = t_j - t_{j-1}\) 表示时间间隔。当 \(X\) 和 \(\Omega\) 均视为可通过观测获得时,便构成了完全数据。此时,对应的完全对数似然函数为:
要想获得模型参数的最大似然估计,主要的难点在于需要最大化对数似然函数(即上式(4.2))
由于隐变量 \(\Omega\) 是不可观测的,直接对上述对数似然函数进行约束优化在计算上很难实现,通常无法收敛到一个解。因此,有必要寻求一种更有效的算法来处理该问题。EM(Expectation-Maximization)算法为我们提供了一种解决该难题的可行方法。
在数据不完全或有缺失值时,EM算法能够通过给定的数据集找到潜在分布参数的极大似然估计。该算法的基本思想是利用可观测数据的条件期望来代替隐变量 \(\Omega\)。在算法迭代的每一步,能够以封闭的形式或直接的方式获得更新的参数估计。通过这种方式,EM算法能够逐步逼近潜在分布参数的最大似然估计。
EM算法通常由两个基本步骤通过反复迭代完成。首先,该算法关于隐变量计算对数似然函数的期望,这一步骤通常被称为E-step;然后,对求过期望后的对数似然函数进行最大化,这一步骤通常被称为M-step。上述两个步骤通过迭代反复进行,直至达到指定的收敛准则为止。与其它优化方法相比,EM算法的优点在于其不仅计算上相对简单,而且能够保证收敛。
通过上面对EM算法的介绍可知,该算法隐含的一个假设是必须保证隐变量能够通过监测的退化数据来估计。对于我们要解决的问题这一条件满足。假设\(\Theta^{(k)} = [\mu_{\beta}^{(k)}, \tau_{\beta}^{2(k)}, \sigma^{2(k)}]\)表示在第\(i\)步基于退化数据\(\mathbf{X}\)对模型未知参数的估计值。如前所述,假设漂移参数\(\beta_i\)服从均值为\(\mu_{\beta}\)方差为\(\tau_{\beta}^2\)的正态分布。因此,在已知\(\mathbf{X}_i\)和\(\Theta^{(k)}\)的条件下,\(\beta_i\)的后验估计仍然服从正态分布,其均值记为\(\mu_i^{(k)}\),方差记为\(\tau_i^{2(k)}\)。
在Bayesian框架下,\(\beta_i\)的后验分布可以很容易地通过Bayesian公式进行更新。相关公式表示如下:
在已知\(\mathbf{X}_i\)和\(\Theta^{(k)}\)的条件下,根据\(\beta_i\)服从正态分布的性质,可以得到
其中
因此,我们可以自适应地调整参数 \((\mu_i, \sigma_i^2)\),通过迭代更新来降低不确定性,并使其更接近新的漂移参数。下面将描述如何利用EM算法来迭代地找到模型未知参数 \(\Theta\) 的最大似然估计 \(\hat{\Theta} = (\hat{\mu}_{\beta}, \hat{\tau}_{\beta}^2, \hat{\sigma}^2)\)。
在已知退化数据 \(\mathbf{Y}\) 和当前的参数估计值 \(\Theta^{(k)}\) 的情况下,EM算法的工作流程如下:
-
E-step:计算关于隐变量 \(\Omega\) 的完全对数似然函数 \(\mathcal{L}(\Theta | \mathbf{Y}, \Omega)\) 的期望 \(\mathbb{Q}(\Theta | \mathbf{Y}, \Theta^{(k)})\)。具体地,该期望可以表示为:
\[\begin{align*} \mathcal{Q}(\Theta|\mathbf{Y},\Theta^{(k)}) &= E_{\Omega|\Theta^{(k)}}[\mathcal{L}(\Theta|\mathbf{Y},\Omega)]\\ &= -\frac{1}{2} \sum_{i=1}^{n} \left[ (m+1) \ln{2\pi} + \sum_{j=1}^{m} \ln{\Delta t_j} + m \ln{\sigma^2} + \ln{\tau_{\beta}^2} \right.\\ &\quad \left. + \sum_{j=1}^{n} \frac{(\Delta X_{ij})^2 - 2\mu_i^{(k)} \Delta X_{ij} \Delta t_j + (\Delta t_j)^2 ((\mu_i^{(k)})^2 + \sigma_i^{2(k)})}{\sigma^2 \Delta t_j}\right.\\ &\quad +\left.\frac{(\mu_i^{(k)})^2 + \sigma_i^{2(k)} - 2\mu_i^{(k)} \mu_{\beta} + \mu_{\beta}^2}{\tau_{\beta}^2} \right] \end{align*} \]这一步的目的是基于当前的参数估计值 \(\Theta^{(k)}\) 和观测数据 \(\mathbf{Y}\),来计算隐变量 \(\Omega\) 的分布,并据此求出完全对数似然函数的期望。
-
M-step:在E-step获得的期望 \(\mathbb{Q}(\Theta | \mathbf{Y}, \Theta^{(k)})\) 的基础上,进行最大化操作,令\(\frac{\partial Q(\Theta | Y, \Theta^{(k)})}{\partial \Theta} = 0\),则可求得最新的参数估计值 \(\Theta^{(k+1)}\),其中
通过不断地迭代E-step和M-step,我们可以逐步逼近模型未知参数 \(\Theta\) 的最大似然估计值 \(\hat{\Theta}\)。多次迭代后,产生一系列的估计值 \(\{\Theta^{(0)}, \Theta^{(1)}, \ldots\}\),直到满足收敛准则,获得真实参数值 \(\Theta\) 的一个好的近似 \(\hat{\Theta} = (\hat{\mu}_{\beta}, \hat{\tau}_{\beta}^{2}, \hat{\sigma}^{2})\)。迭代终止取两次更新获得的参数 \(\Theta^{(k)}\) 和 \(\Theta^{(k+1)}\) 之间的差百分比小于一个预先指定的阈值。对整个过程的描述如算法4.1所示,\(th\) 为给定的迭代终止阈值。
初始化 \(\mu_\beta^{(0)}\),\(\tau_\beta^{2(0)}\),\(\sigma^{2(0)}\)。
while (\(|\Theta^{(k)}-\Theta^{(k+1)}|\)):
根据式(4.4)和式(4.5)计算得到 \(\mu_i^{(k)}\),\(\sigma_i^{2(k)}\)
利用式(4.6)、式(4.7)和式(4.8)更新 \(\mu_\beta^{(k+1)}\)、\(\tau_\beta^{2(k+1)}\)和\(\sigma^{2(k+1)}\)
end
获得最大似然估计\(\hat{\Theta}=(\hat{\mu}_\beta,\hat{\tau}_\beta^2,\hat{\sigma}^2)\)
通过MATLAB代码得到,在阈值\(th=10^{-6}\)情况下,\(\hat{\mu}_\beta=0.002037906666667\),\(\hat{\tau}_\beta=0.000417742406470\),\(\hat{\sigma}=0.010800005576587\)。
2.4.2 可靠性函数\(R(t)\)推导
以下借鉴了论文潘东辉.基于退化数据的产品可靠性建模与剩余寿命预测方法研究[D].华中科技大学,2014.
在2.2节中,我们已经得到了漂移参数为常量 \(\mu\) 的可靠度函数,即下式(2.3)。
针对漂移参数 \(\beta\) 服从正态分布的情况,即 \(\beta\sim N(\mu_\beta, \tau_\beta^2)\) ,推导了此时寿命 \(T\) 对应的PDF和可靠度函数。为了简化推导过程,首先给出下面这个命题4.1。
命题4.1 若 \(Z\sim N(\mu,\sigma^2)\) 和 \(c,\gamma,\lambda\in\mathbb{R}\),则下式(4.9)成立
证明: 在 \(X\sim N(0,1)\) 和 \(a,b\in\mathbb{R}\) 的条件下,有 \(E_X[\Phi(a+bX)]=\Phi(a/\sqrt{1+b^2})\)。因此,利用 \(x=(z-\mu)/\sigma\) 进行变量替换,得以得到
故得证。
下式(4.10)右侧第一项,使用了结论:在 \(X\sim N(\mu,\sigma^2)\) 且 \(a,b\in\mathbb{R}\) 的条件下,可得 \(E_X[\Phi(a+bX)]=\Phi((a+b\mu)/\sqrt{1+b^2\sigma^2})\)。结合上面的命题4.1可以得到寿命 \(T\) 的可靠度函数 \(R(t)\)。通过对 \(R(t)\) 求导,可以得到寿命 \(T\) 的PDF。
2.4.3 代码部分
2.4.3.1 分析
EM部分:
式(4.4)与式(4.5)易于计算,重点在于式(4.6),式(4.7)和式(4.8)。
进行一定的变换
其中\(\sum_{i=1}^{n} \sum_{j=1}^{m}\frac{(\Delta X_{ij})^2}{\Delta t_j}\)只与数据集有关,在数据集一定的情况下为常量,可以提前算出。令
即可得到
代码中\(N\)为样本数,\(M\)为每个样本观测次数,注意,\(m=M-1\),因为上述分析过程中的\(m\)是从0开始的。
可靠度函数 \(R(t)\) 部分:
首先采用同2.2节的方法,尝试通过式(4.10)直接求得可靠度函数 \(R(t)\),结果无法绘制出图像,反复检查式子依然无果,甚至开始怀疑论文写错了,然后去找了这篇论文参考的论文,推了一下,发现没错,输出调试发现式(4.10)中 \(\exp(x)\) 的参数 \(\frac{2\mu_\beta D}{\sigma^{2}} + \frac{2\tau_\beta^2 D^2}{\sigma^{4}}\) 达到了 \(2914\),怀疑精度出现问题。意外发现若将该式子 \(\exp(x)\) 中的参数只取前一项即 \(\frac{2\mu_\beta D}{\sigma^{2}}\approx 350\),计算结果在 \(0\sim1\)范围内。即说明其后的 \(\Phi \left( -\frac{\sigma^{2}(\mu_\beta t + D) + 2\tau_{\beta}^{2}Dt}{\sigma^{2}\sqrt{\sigma^{2}t + \tau_{\beta}^{2}t^{2}}} \right)\) 与漂移参数为常量时对应项 \(\Phi\left(-\frac{\mu t+D}{\sigma\sqrt{t}}\right)\) 数量级相同,而 \(\Phi(x)\) 自变量的值由原先的约 \(-23\) 变动至约 \(-76\),故确定为 \(\Phi(x)\) 的精度炸了。
发现 \(R(t)\) 对 \(t\) 求导得到概率密度函数 \(f(t)\)(式(4.11))中不存在 \(\Phi(x)\),且计算过程较为简单,故尝试计算出 \(f(t)\) 后通过累加法求出 \(R(t)\),成功。
2.4.3.2 代码实现
Laser_dat = readtable('GaAsLaser.csv');
N = 15;
M = 17;
MM = 8001; % 概率密度函数观察次数
D = 10; % 失效阈值
Tim = linspace(0, 8000, MM); % 观测时间点
format long;
x = zeros(N, M); % x: Percent Increase
t = zeros(N, M); % t: Hours
for i = 1 : N
for j = 1 : M
x(i, j) = Laser_dat.PercentIncrease((i - 1) * M + j);
t(i, j) = Laser_dat.Hours((i - 1) * M + j);
end
end
Xm = zeros(1, N); % \sum_j{\Delta X_{ij}} = \Delta X_{im}
tm = zeros(1, N); % \sum_j{\Delta t_{ij}} = \Delta t_{im}
SSX2dt = 0; % \sum_i\sum_j{\dfrac{(\Delta Y_{ij})^2}{\Delta t_{ij}}}
for i = 1 : N
for j = 1 : M - 1
SSX2dt = SSX2dt + (x(i, j + 1) - x(i, j))^2 / (t(i, j + 1) - t(i, j));
end
Xm(i) = x(i, M);
tm(i) = t(i, M);
end
% EM迭代
a = 1; % a = \mu_\beta
b = 1; % b = \tau_\beta^2
c = 1; % c = \sigma^2
th = 1e-6; % 迭代终止阈值
Delta = inf; % 迭代差值
cnt = 0; % 迭代次数
e1 = zeros(1, N); % Ei = \sum{ei}
e2 = zeros(1, N);
e3 = zeros(1, N);
while (Delta >= th)
cnt = cnt + 1;
A = a; % A = \mu_\beta(k)
B = b; % B = \tau_\beta^2(k)
C = c; % C = \sigma^2(k)
% E-step
for i = 1 : N
mui = (Xm(i) * B + A * C) / (tm(i) * B + C);
sigmai2 = (C * B) / (tm(i) * B + C);
e1(i) = mui;
e2(i) = mui^2 + sigmai2;
e3(i) = -2 * mui * Xm(i) + (mui^2 + sigmai2) * tm(i);
end
E1 = sum(e1); % \sum{\mu_i^{(k)}}
E2 = sum(e2); % \sum{(\mu_i^{(k)})^2+\sigma_i^{2(k)}}
E3 = sum(e3); % \sum{-2\mu_i^{(k)}\sum_j{\Delta X_{ij}} + [(\mu_i^{(k)})^2+\sigma_i^{2(k)}]\sum_j{\Delta t_{ij}}}
% M-step
a = E1 / N;
b = (E2) / N - a^2;
c = (SSX2dt + E3) / N / (M - 1);
Delta = max([abs(A - a) / a, abs(B - b) / b, abs(C - c) / c]);
end
mu = a; tau = sqrt(b); sigma = sqrt(c);
[mu, tau, sigma]
% R(t)
F = zeros(1, MM);
f = zeros(1, MM);
for i = 1 : MM
ti = Tim(i);
% R(i) = phi((D - mu * ti) / sqrt(sigma^2 * ti + tau^2 * ti^2)) - exp((2 * mu * D) / (sigma^2) + (2 * tau^2 * D^2) / (sigma^4)) ...
% * phi(-(sigma^2 * (mu * ti + D) + 2 * tau^2 * D * ti) / (sigma^2 * sqrt(sigma^2 * ti + tau^2 * ti^2)));
f(i) = D / sqrt(2 * pi * ti^3 * (tau^2 * ti + sigma^2)) * exp(-(D - mu * ti)^2 / (2 * ti * (tau^2 * ti + sigma^2)));
if (i > 1)
F(i) = F(i - 1) + (Tim(i) - Tim(i - 1)) * f(i);
end
end
figure;
subplot(1, 2, 1); % f(t)
hold on;
plot(Tim, f, 'Color', 'red', 'LineWidth', 1);
title('The distribution function for D = 10');
xlabel('Time(hour)');
ylabel('PDF');
legend('f(t)', 'Location', 'best');
hold off;
subplot(1, 2, 2); % R(t)
hold on;
plot(Tim, 1 - F, 'Color', 'red', 'LineWidth', 1);
title('The reliability function for D = 10');
xlabel('Time(hour)');
ylabel('Reliability');
legend('R(t)', 'Location', 'best');
hold off;
function res = phi(x)
res = 1 / 2 * (1 - erf(-x / sqrt(2)));
end
2.4.3.3 输出
阈值\(th=10^{-6}\)情况下,
\(\hat{\mu}_\beta=0.002037906666667\)
\(\hat{\tau}_\beta=0.000417742406470\)
\(\hat{\sigma}=0.010800005576587\)

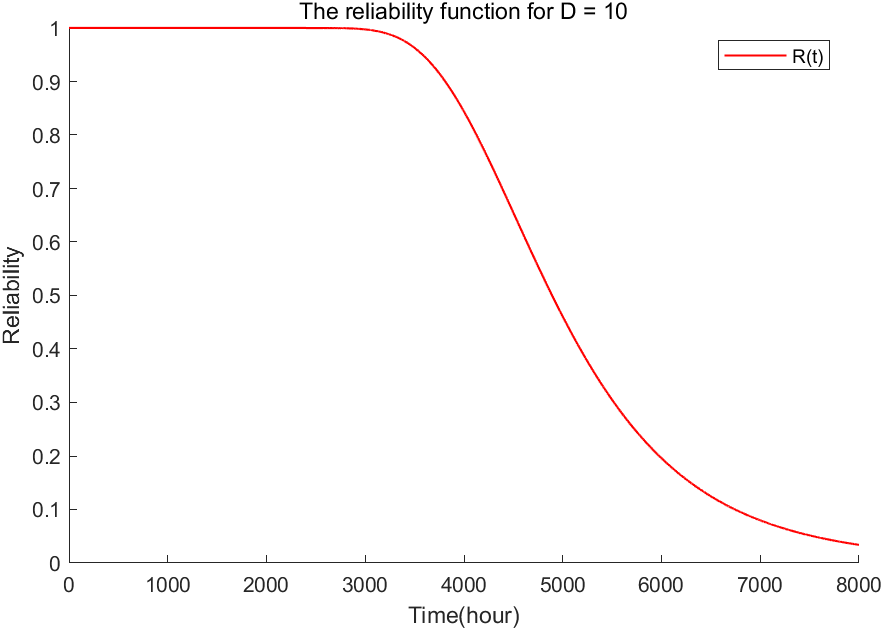
2.5 扩展
2.5.1 建模计算分析
以下借鉴了论文徐廷学,王浩伟,张鑫.EM 算法在 Wiener 过程随机参数的超参数值估计中的应用[J].系统工程与电子技术, 2015, 37(3):6.
以下需要注意检查所有的\(Y\)是否改为了\(X\),下标的\(n\)应为\(m\),\(\Lambda(t_i)\)应为\(t_i\)
为了更好的解释器件之间的异质性,在假设\(\beta\)遵从\(\beta\sim N(\mu,\tau^2)\)之外,假设参数\(\sigma\)也遵从一定的分布。令\(\omega=\frac{1}{\sigma^2}\),假定\(\omega\)遵从Gamma分布。即假设\(\mu\)和\(\omega(\omega=\frac{1}{\sigma^2})\)服从如下共轭先验分布:
式中,\(a, b, c, d\) 为超参数。当得到现场退化数据 \(\mathbf{X} = (X_1, X_2, \cdots, X_n)\) 后,超参数的后验估计可由 Bayesian 公式推导出。
式中,\(\mathcal{L}(\mathbf{X} \mid \mu, \omega)\) 为极大似然函数;\(\pi(\mu, \omega)\) 为 \(\mu, \omega\) 的联合先验密度函数;\(\pi(\mu, \omega \mid \Delta \mathbf{X})\) 为联合后验密度函数。
代入式(5.2),则
因为随机参数的共轭先验分布与其后验分布具有相同的分布函数,区别只是超参数值的变化。据此,可从式(5.3)中推导出超参数的后验估计值 \(a^{*}\), \(b^{*}\), \(c^{*}\), \(d^{*}\) 为
PS.论文中\(a^* = \frac{n}{2} + a\),怀疑是笔误(论文中的N,n即为本文中的n,m)
以下采用EM算法,获取超参数先验估计值。设 $ X_{ij} $ 为第 $ i $ 个样品经第 $ j $ 次测量得到的退化数据,$ t_{ij} $ 为相应的测量时刻,其中 $ i = 1, 2, \cdots, n; j = 1, 2, \cdots, m $。将所有 $ (y_{ij}, t_{ij}) $ 作为先验信息,建立一个如下包含参数 $ \mu_i, \omega_i $ 和超参数 $ a, b, c, d $ 的完全似然函数。
可得超参数的极大似然估计,其中\(\hat{a}\)可由下式(5.6)解出
式中,\(\psi(\cdot)\)为digamma分布函数。\(\hat{b}, \hat{c}, \hat{d}\)的解析式为
在式(5.6)和式(5.7)中,\(\mu_i\) 和 \(\omega_i\) 为隐含数据,因此 \(\hat{a}, \hat{b}, \hat{c}, \hat{d}\) 无法直接解出。通过EM算法求解时,首先需要设定超参数的一组初值,然后通过若干次递归迭代来求解。EM算法的工作流程如下:
- E-step:根据 \(\omega_i\) 服从Gamma分布,而条件分布 \(\mu_i|\omega_i\) 服从正态分布,可以进一步推出 \(\mu_i\) 服从非中心\(t\)分布。需要求出以下期望值:\(E(\omega_i), E(\ln \omega_i), E(\omega_i \mu_i), E(\omega_i \mu_i^2)\)。假设 \(\hat{a}_k, \hat{b}_k, \hat{c}_k, \hat{d}_k\) 是经过\(k\)次迭代后得到的估计值,那么在第\((k+1)\)次迭代过程中:
- M-step:在M步中,将E步中求得的各项期望值代入式(5.6)和式(5.7),即可得到在\((k+1)\)步迭代后的超参数估计值 \(\hat{a}_{k+1}, \hat{b}_{k+1}, \hat{c}_{k+1}, \hat{d}_{k+1}\),其解析式如下:
通过不断地迭代E-step和M-step,我们可以逐步逼近模型未知参数 \(a, b, c, d\) 的最大似然估计值 \(\hat{a}, \hat{b}, \hat{c}, \hat{d}\),迭代终止取两次更新获得的参数 \(\hat{a}_{k}, \hat{b}_{k}, \hat{c}_{k}, \hat{d}_{k}\) 和 \(\hat{a}_{k-1}, \hat{b}_{k-1}, \hat{c}_{k-1}, \hat{d}_{k-1}\) 之间的差百分比小于一个预先指定的阈值。算法框架基本同算法4.1,此处略,\(th\)为给定的迭代终止阈值。
通过MATLAB代码得到,在阈值\(th=10^{-6}\)情况下,\(\hat{a}=5.354565020643575\),\(\hat{b}=0.000485988543804\),\(\hat{c}=0.001956129531677\),\(\hat{d}=0.001508611444841\)。
2.5.2 代码部分
2.5.2.1 代码实现
Laser_dat = readtable('GaAsLaser.csv');
M = 17;
N = 15;
format long;
x = zeros(N, M); % x: Percent Increase
t = zeros(N, M); % t: Hours
for i = 1 : N
for j = 1 : M
x(i, j) = Laser_dat.PercentIncrease((i - 1) * M + j);
t(i, j) = Laser_dat.Hours((i - 1) * M + j);
end
end
Xm = zeros(1, N); % \sum_j{\Delta X_{ij}} = \Delta X_{im}
tm = zeros(1, N); % \sum_j{\Delta t_{ij}} = \Delta t_{im}
SX2dt = zeros(1, N); % \sum_j{\dfrac{(\Delta Y_{ij})^2}{\Delta t_{ij}}}
for i = 1 : N
for j = 1 : M - 1
SX2dt(i) = SX2dt(i) + (x(i, j + 1) - x(i, j))^2 / (t(i, j + 1) - t(i, j));
end
Xm(i) = x(i, M);
tm(i) = t(i, M);
end
% EM迭代
a = 1; b = 1; c = 1; d = 1;
th = 1e-6;
Delta = inf;
cnt = 0;
e1 = zeros(1, N);
e2 = zeros(1, N);
e3 = zeros(1, N);
e4 = zeros(1, N);
while (Delta >= th)
cnt = cnt + 1;
A = a; B = b; C = c; D = d;
% E-step
for i = 1 : N
a_ = A + M / 2;
b_ = B + (C^2 / D - (D * Xm(i) + C)^2 / (D^2 * tm(i) + D) + SX2dt(i))/2;
c_ = (D * Xm(i) + C) / (D * tm(i) + 1);
d_ = D / (D * tm(i) + 1);
e1(i) = a_ / b_;
e2(i) = psi(a_) - log(b_);
e3(i) = e1(i) * c_;
e4(i) = e1(i) * c_^2 + d_;
end
E1 = sum(e1); % E(\omega_i)
E2 = sum(e2); % E(\ln\omega_i)
E3 = sum(e3); % E(\omega_i\mu_i)
E4 = sum(e4); % E(\oemga_i\mu_i^2)
% M-step
fun1 = @(x)psi(x) - log(x) - E2 / N - log(N) + log(E1);
a = fsolve(fun1, 1e-5);
b = N * a / E1;
c = E3 / E1;
d = (E4 - 2 * c * E3 + c^2 * E1) / N;
Delta = max([abs(A - a) / a, abs(B - b) / b, abs(C - c) / c, abs(D - d) / d]);
end
[a, b, c, d]
2.5.2.2 输出
阈值\(th=10^{-6}\)情况下,
\(\hat{a}=5.354565020643575\)
\(\hat{b}=0.000485988543804\)
\(\hat{c}=0.001956129531677\)
\(\hat{d}=0.001508611444841\)
参考文献
[1]金光.基于退化的可靠性技术——模型、方法及应用[M].国防工业出版社,2014.
[2]潘东辉.基于退化数据的产品可靠性建模与剩余寿命预测方法研究[D].华中科技大学,2014.
[3]徐廷学,王浩伟,张鑫.EM 算法在 Wiener 过程随机参数的超参数值估计中的应用[J].系统工程与电子技术, 2015, 37(3):6.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号