数据质量分析

题目描述：进行数据质量分析

数据质量分析是数据预处理的前提，也是数据挖掘分析结论有效性和准确性的基础。其主要任务是检查原始数据中是否存在脏数据：

（1）缺失值检测

1.代码如下：

import pandas as pd
import numpy as nm
import matplotlib.pyplot as plt

data = pd.read_csv(r"D:/software/Sublime Text Build 3059 x64/ss.csv",usecols=[0,1],encoding='gb2312')

# num = pd.Series(data,index=[i in range(size(data))])
print(data.describe())
data_value = data['销量'].shape[0] - data['销量'].count()
print("缺失值数量：",data_value)
print("样本个数：",data['销量'].shape[0])
# print(data.isnull())
print(data.info())

 

2.运行结果：

 3.结果分析：

可以看出在这个数据集中样本个数为201个，其中缺失值为1 个。

 

（2）异常值（outliers）分析

异常值是指样本中数值明显偏离其余观测值的个别值，也称为离群点。

1、简单统计量分析

先对变量做描述性统计，检查数据是否合理。常用的统计量是最大、最小值，极差等。

 

1.代码如下：

mport pandas as pd
import csv
import matplotlib.pyplot as plt
import numpy as np

df_data = pd.read_csv('D:/software/Sublime Text Build 3059 x64/ss.csv',encoding='gb18030',) 
print(df_data.describe())
print("data size: {}".format(df_data.shape))
max=df_data.max()
min=df_data.min()
mean=df_data.mean()
print("最大值:",max)
print("最小值:",min)
print("平均值:",mean)

# （1）求极差
# 极差 = 最大值 - 最小值
data=df_data['销量'].describe()
data_range = (data.max()-data.min())
print("极差：{}".format(data_range))

 

2.运行结果：

 

3.结果分析：

通过运行的结果可以看出此数据集的最大销售数量为2015/3/1的9106.44，最小值为2014/10/1日的22，销售数据的平均值为2755.2147，极差为9084.44。

 

2、箱型图分析

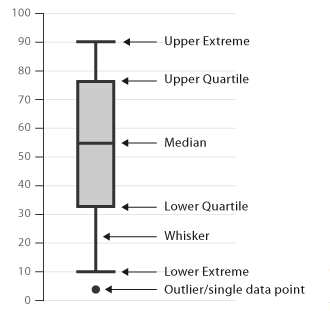
1.箱线图异值定义

 

2. 代码如下：

# -*- coding: utf-8 -*-
import pandas as pd
import matplotlib.pyplot as plt

plt.rcParams["font.sans-serif"] = ["SimHei"] # 显示中文字体
plt.rcParams["axes.unicode_minus"] = False  # 显示负号

data = pd.read_csv(r"D:/software/Sublime Text Build 3059 x64/ss.csv",usecols=[0,1],encoding='gb2312')

plt.figure()
p = data.plot.box(return_type='dict')
x = p["fliers"][0].get_xdata() # flier：异常值标签
y = p["fliers"][0].get_ydata()
y.sort()

# annotate添加注释
for i in range(len(x)):
    if i > 0:
        plt.annotate(y[i], xy=(x[i], y[i]),
                     xytext=(x[i] + 0.05 - 0.8 / (y[i] - y[i - 1]), y[i]))
    else:
        plt.annotate(y[i], xy=(x[i], y[i]), xytext=(x[i] + 0.08, y[i]))

plt.show()
# annotate添加注释
for i in range(len(x)):
    if i > 0:
        plt.annotate(y[i], xy=(x[i], y[i]),
                     xytext=(x[i] + 0.05 - 0.8 / (y[i] - y[i - 1]), y[i]))
    else:
        plt.annotate(y[i], xy=(x[i], y[i]), xytext=(x[i] + 0.08, y[i]))
plt.show()

 

3.运行结果：

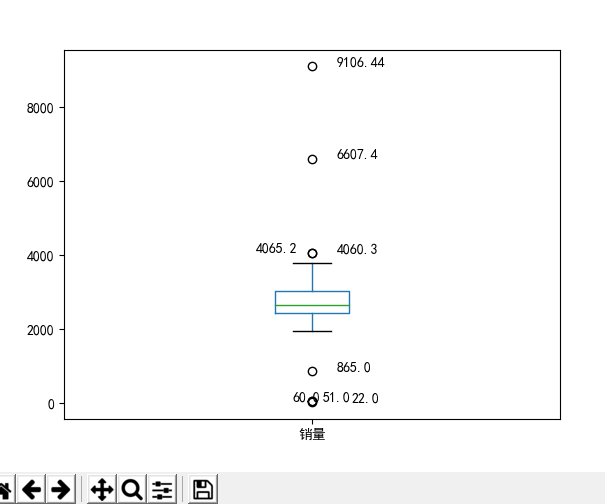
 4.结果分析：

该例中，865、4060.3、4065.2可归为正常值；22、51、60、6607.4、9106.44归为异常值。