Diffusion综述阅读笔记

扩散模型综述

生成模型大观

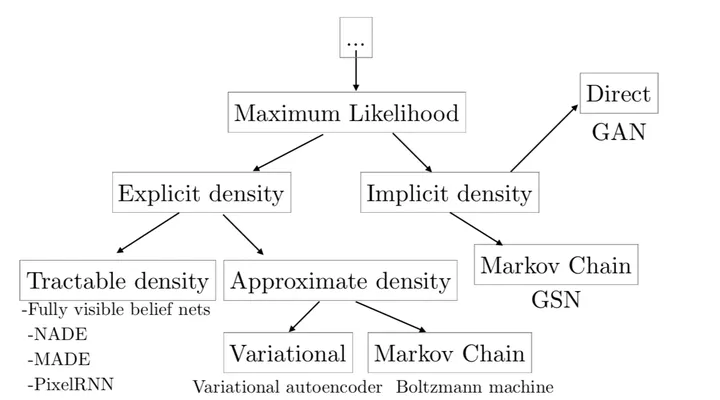
图源 NIPS 2016 Tutorial: Generative Adversarial Networks

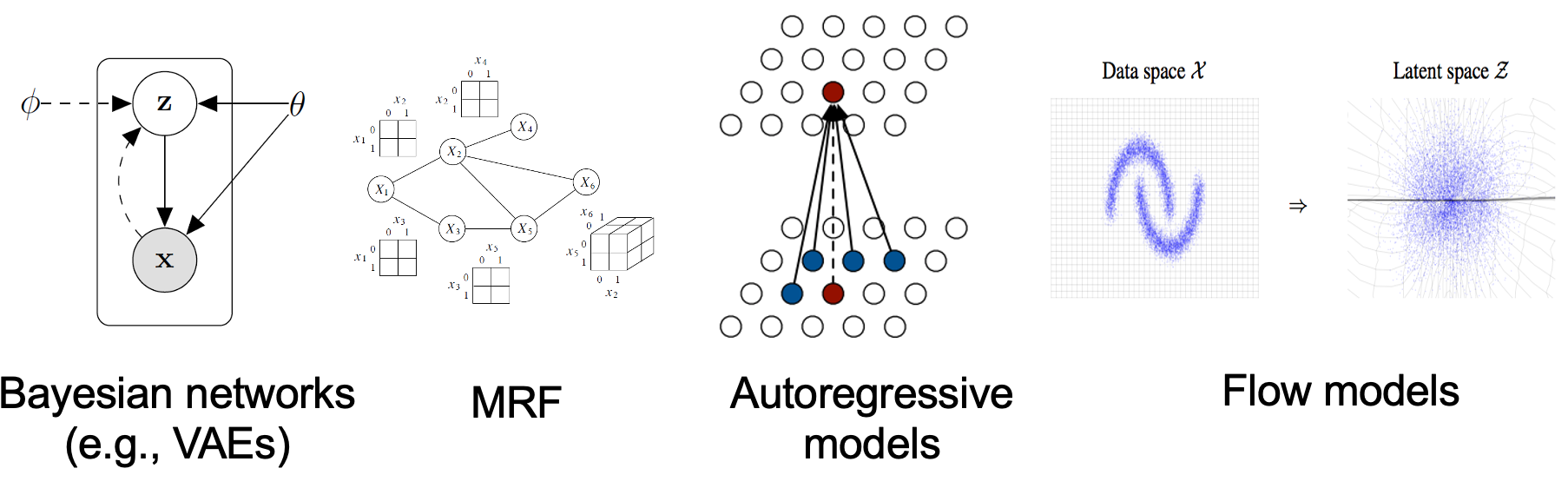
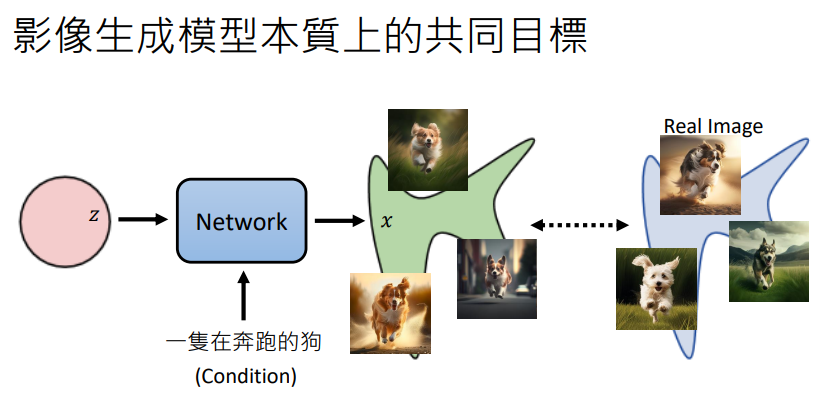
生成模型的本质是在学习数据的概率分布。如果将它想象成包括一个潜在变量 \(z\) 的联合分布模型，通过积分的形式来表示这一分布（边际似然）如下：

\[P_\theta(x)=\int_z P_\theta(x, z)dz=\int_z P(z)P_\theta(x|z)dz \]

其中，\(P(𝑧)\) 一般是标准正态分布，而 \(P_\theta(x|z)\) 可以选择任意的条件高斯分布或者狄拉克分布。这样的积分形式可以形成很多复杂的分布，理论上来讲，它能拟合任意分布。而我们的目标就是使 \(P_\theta(x)\) 最大化。

最大似然

直接对 \(P_\theta(x)\) 做最大似然估计。记从原数据分布 \(P_{data}\) 中随机采样到的数据是 \({x^1, x^2, ..., x^m}\)，则最大化目标就是：

\[\begin{aligned} \theta^*&=arg \max_\theta \prod_{i=1}^m P_\theta(x^i)\\ &\approx arg\max_\theta \mathbb{E}_{x\sim p_{data}(x)}[log\space P_\theta(x)]\\ &=arg \max_\theta\int_x P_{data}(x)log\space P_\theta(x)dx \end{aligned} \]

我们可以加上一个常数项，让它变成一个KL散度：

\[\begin{aligned} \theta^*&\approx arg \max_\theta\int_x P_{data}(x)log\space P_\theta(x)dx\\ &=arg \max_\theta\int_x P_{data}(x)log\space P_\theta(x)dx-arg \max_\theta\int_x P_{data}(x)log\space P_{data}(x)dx\\ &=arg \max_\theta\int_x P_{data}(x)log\frac{P_\theta(x)}{P_{data}(x)}dx\\ &=arg \min_\theta KL(P_{data}(x)||P_\theta(x)) \end{aligned} \]

所以最大似然的本质就是最小化KL散度，当然KL散度是很难算的。

GAN的本质其实就是用变分的方法（加了一个判决器）直接最小化某一个散度。（这一点在 f-GAN 中得到了更进一步的证明，判决器的作用就是一个变分散度估计。）

变分推断与 VAE

传统的自编码器直接用重构损失（通常是均方误差）来优化编码器。

还是原来的问题：

\[P_\theta(x)=\int_z P(z)P_\theta(x|z)dz \]

其中， \(P(𝑧)\) 还是标准正态分布，\(P_\theta(x|z)\) 的 \(\theta\) 就是从隐变量生成数据的解码器 decoder。

直接计算积分依旧是困难的，不过不像GAN避开了这个困难，VAE选择用最大化一个变分推断的证据下界（ELBO）来最大化似然函数。

怎么推断呢？还是熟悉的取对数：

\[\log P_\theta=\log\int_zP(z)P_\theta(x|z)dz \]

接下来引入一个变分分布 \(q_\phi(z|x)\) ：

\[\log P_\theta(x)=\log\int_zq_\phi(z|x)\frac{P(z)P_\theta(x|z)}{q_\phi(z|x)}dz \]

利用 Jensen 不等式，我们可以找到一个下界：

\[\begin{aligned} \log P_\theta(x)&\geq \int_zq_\phi(z|x)\log\frac{P(z)P_\theta(x|z)}{q_\phi(z|x)}dz\\ &=\int_zq_\phi(z|x)\log P_\theta(x|z) +\int_zq_\phi(z|x)\log\frac{P(z)}{q_\phi(z|x)}dz\\ &=E_{q_\phi(z|x)}[\log P_\theta(x|z)]-KL(q_\phi(z|x)||P(z)) \end{aligned} \]

最后优化的目标就是最大化这个下界，也就是证据下界（ELBO）。放在自编码器的结构里， \(q_\phi(z|x)\) 就是编码器。于是这个目标也可以解释为最小化解码器重构误差和最小化编码隐变量的KL散度（鼓励数据的多样性）。

最后一个问题还没有解决：既然要算期望，就需要采样，采样是一个完全随机的过程，也就是不可反向传播的，于是VAE采用了重参数化技巧来解决这一问题，允许我们使用梯度下降法在采样的数据进行似然函数的优化。

什么是重参数化呢？简单来说就是让模型学习分布的参数，把采样的压力转嫁给一个随机变量。鼎鼎大名的 Gumble-Softmax 就是一个典型例子。

具体而言，假定编码器输出的隐变量的分布是一个多元正态分布，参数为 \(\mu\) 和 \(\sigma^2\) ：

\[q_\phi(z|x)=\mathcal{N}(\mu,\sigma^2\mathbb {I}) \]

重参数化的采样就是先从一个独立的标准正态分布里采样一个随机向量 \(\epsilon\) ，那我们从模型参数中采样隐变量的过程就是：

\[z=\mu+\sigma\space\odot \space\epsilon \]

VAE相比于GAN最大的优势是模型的损失是一致的，没有对抗训练，而GAN的各种缺点基本上都是对抗带来的。不过VAE假设分布是高斯分布也有一定的局限性。

能量模型

当然，生成模型也可以从别的角度建模，另一个常用的角度是从能量模型的角度解释，人们尝试用玻尔兹曼分布来描述它：

\[P_\theta(x)=\frac{e^{-f_\theta(x)}}{Z_\theta} \]

其中， \(f_\theta\) 是带参数 \(\theta\) 的未定函数，称为“能量函数 (energy-based model)” 或未正则化概率模型，可以把它解释为采样到 \(x\) 的难易程度，能量越低，采样到的概率就越高。 \(Z_\theta\) 是配分函数，或者说归一化因子，其目的是为了保证概率函数的合法性 \(\int P_\theta(x)dx=1\)，其值是一个取决于 \(\theta\) 的常数，有：

\[Z_\theta=\int e^{-f_\theta(x)}dx \]

训练网络的目标其实还是最大似然：

\[\theta^*=\arg \max_\theta \sum_{i=1}^N \log p_\theta(x_i) \]

同样是因为积分的存在，优化中最大的困难是配分函数 \(Z_\theta\) 很难显式地计算出来，尤其是在高维的情况下。

一般来说会限制模型架构（如因果卷积）或近似求 \(Z_\theta\) 来求解（如 VAE 、MCMC采样）。

扩散模型

发展历史

在2008年就已经有了去噪自编码器的模型DAE，可见去噪并不是一个很新的想法，不过这么模型的目标是从加噪的数据中重构出原始数据，实际的应用场景比较有限，一般用在用噪声把控特征尺度的特征提取上（AE的设计就是为了提取特征而生的）。

Diffusion Model 出生在2015年的论文 Deep Unsupervised Learning using Nonequilibrium Thermodynamics (arxiv.org) 中，比 GAN 晚一年，但由于 GAN 的想法过于有趣并且确实很 work ，DM 的知名度一直不太高。

2019年，宋飏老师发布Score-based model。

2020年6月，DDPM 发布，首次展现出能媲美GAN的生成效果；10月，DDIM发布，用确定性采样加速了图像的迭代过程。（GAN Inversion）

2021年2月，宋飏老师在论文中从随机微分方程的视角统一了去噪扩散和Score-based model，同时，OpenAI 发布Improved Diffusion；5月，OpenAI 发布Classifier Guidance，即通过基于分类器的引导来指导扩散模型生成图像。借助其他多项改进，扩散模型首次成功击败了生成领域的巨头“GAN”，同时也为DALLE-2（一个图像和文本生成模型）的发布奠定了基础。

接下来是不断从模型各个方面进行优化，这一阶段我认为最重要的工作还是 DDIM 的 respacing 加速采样。

另一边离散扩散以 2021年7月的 D3PM 为代表，虽然在不断探索，但实际效果还比较一般。

2022年下半年，Stable-Diffusion 出圈， LDM 横扫工业界。

2023 年，CM 模型及其后的一系列模型被提出，加速采样效果拔群。

直观理解

扩散的概念来自于物理学的布朗运动。

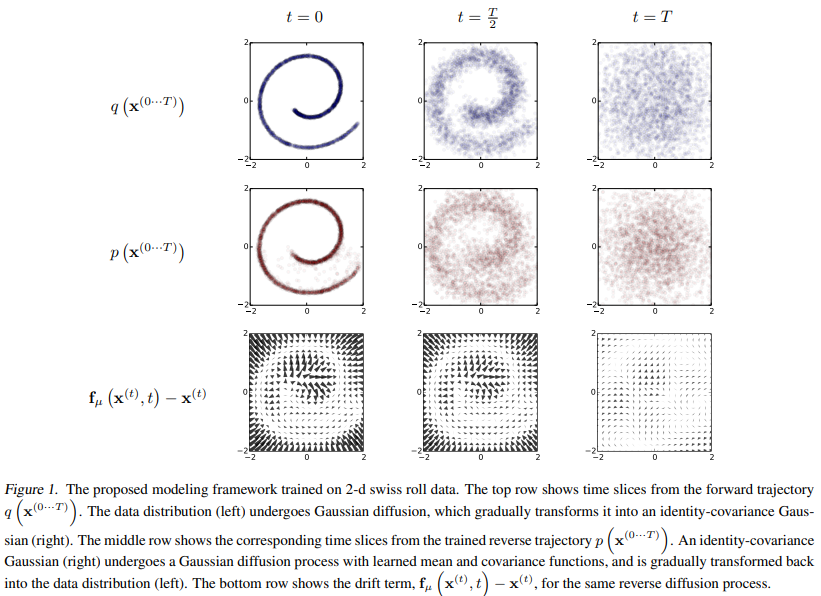
此图来源于2015年的原始论文。

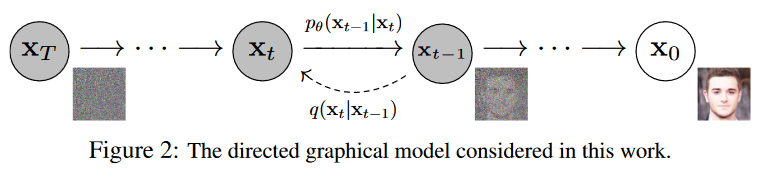
此图来源于2020年的DDPM。

前向过程：每一步给图像添加一个噪声，到第 \(T\) 步时噪声完全破坏了原图的结构信息。

后向过程：每一步，模型输入加噪声的图像，预测一个噪声。在减噪声的时候也有一个采样过程。

一般来说，加的噪声是高斯噪声。

数学解释

扩散模型是一种潜变量模型，其形式为 \(p_\theta(x_0):=\int p_\theta(x_{0:T})dx_{1:T}\) ，其中 \(x_1, ...x_T\) 是与真实数据 \(x_0\sim q(x_0)\) 维度相同的潜变量模型。

前向过程

近似后验过程 \(q(x_{1:T}|x_0)\) 不断加噪声破坏图像结构的过程叫前向过程（forward process）或扩散过程：

\[q(x_{1:T}|x_0):=\prod^T_{t=1}q(x_t|x_{t-1}),\space\space\space q(x_t|x_{t-1}):=\mathcal{N}(x_{t};\alpha_tx_{t-1},\beta_t^2\mathbb {I}) \]

对这个过程中的每一步进行重参数化，每一步以方差表 \(\beta_1, ...\beta_t\) 作为系数给图像加一个高斯噪声 \(\epsilon_t\) ：

\[x_t=\alpha_tx_{t-1}+\beta_t\epsilon_t,\space\epsilon_t\sim\mathcal{N}(0, \mathbb {I}) \]

其中两个系数满足 \(\alpha_t^2+\beta_t^2=1\) 。这是为了计算方便设计的，将上式进行递推：

\[\begin{aligned} x_t &=\alpha_t x_{t-1}+\beta_t\epsilon_t\\ &=\alpha_t(\alpha_{t-1}x_{t-2}+\beta_{t-1}\epsilon_{t-1})+\beta_t\epsilon_t\\ &=...\\ &=(\alpha_t...\alpha_1)x_0+(\alpha_t..\alpha_2)\beta_1\epsilon_1+(\alpha_t..\alpha_3)\beta_2\epsilon_2+...+\alpha_t\beta_{t-1}\epsilon_{t-1}+\beta_t\epsilon_t \end{aligned} \]

其中 \((\alpha_t..\alpha_2)\beta_1\epsilon_1+(\alpha_t..\alpha_3)\beta_2\epsilon_2+...+\alpha_t\beta_{t-1}\epsilon_{t-1}+\beta_t\epsilon_t\) 是多个独立的正态分布之和，也是一个正态分布，其均值为0、方差为 \((\alpha_t..\alpha_2)^2\beta_1^2+(\alpha_t..\alpha_3)^2\beta_2^2+...+\alpha_t^2\beta_{t-1}^2+\beta_t^2\) 。

还可以推出：

\[(\alpha_t...\alpha_1)^2 +(\alpha_t..\alpha_2)^2\beta_1^2+(\alpha_t..\alpha_3)^2\beta_2^2+...+\alpha_t^2\beta_{t-1}^2+\beta_t^2=1 \]

所以采样 \(x_t\) 的过程就是：

\[x_t=\bar{\alpha}_tx_0+\bar{\beta}_t\bar{\epsilon}_t,\space\bar\epsilon_t\sim\mathcal{N}(0, \mathbb {I}) \]

也就是说采样 \(x_t\) 只需要依赖 \(x_{0}\) 。也可以写成：

\[q(x_t|x_0):=\mathcal{N}(x_t;\bar\alpha_t x_0, \bar\beta_t^2\mathbb {I}) \]

其中：

\[\bar\alpha_t:=\prod_{s=1}^t\alpha_s,\space\space \bar\beta_t=\sqrt{1-\bar\alpha_t^2} \]

此处的 \(\alpha\) 和 \(\beta\) 仅为推导方便，和 DDPM 论文的设定是不同的。将此前用的符号写为 \(a\) 和 \(b\) ，则 DDPM 论文里的 \(\alpha\) 和 \(\beta\) 就是：

\[\beta_t=b_t^2,\space \alpha_t:=1-\beta_t=1-b_t^2=a_t^2,\\ \bar\alpha_t=\bar a_t^2=1-\bar b_t^2=\prod_{s=1}^t\alpha_s \]

后验扩散条件概率 \(q(x_{t-1}|x_t, x_0)\) 也是一个高斯分布：

\[q(x_{t-1}|x_t,x_0)=\mathcal{N}(x_{t-1};\tilde{\mu}_t(x_t,x_0),\tilde{\beta}_t\boldsymbol{I}) \]

其中：

\[\tilde{\mu}_t(x_t,x_0):=\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}x_0+\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_t \text{ and } \tilde\beta_t:=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t \]

推导：

\[\begin{aligned} &q(x_{t-1}|x_t,x_0)=q(x_t|x_{t-1}, x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}\\ &\propto \exp \left( -\frac{1}{2} \left( \frac{(x_t - \sqrt{\alpha_t} x_{t-1})^2}{\beta_t} + \frac{(x_{t-1} - \sqrt{\bar\alpha_{t-1}} x_0)^2}{1 - \bar{\alpha}_{t-1}} - \frac{(x_t - \sqrt{\bar\alpha_t} x_0)^2}{1 - \bar{\alpha}_t} \right) \right)\\ &= \exp \left( -\frac{1}{2} \left( \left( \frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}} \right) x_{t-1}^2 - 2 \left( \frac{\sqrt{\alpha_t}}{\beta_t} x_t + \frac{\sqrt{\bar\alpha_{t-1}}}{1 - \bar{\alpha}_{t-1}} x_0 \right) x_{t-1} + C(x_t, x_0) \right) \right) \end{aligned} \]

根据二次函数的性质，可以计算 \(x_{t-1}\) 的均值和方差：

\[\begin{aligned} \tilde{\mu}_t(x_t,x_0)&=\left( \frac{\sqrt{\alpha_t}}{\beta_t} x_t + \frac{\sqrt{\bar\alpha_{t-1}}}{1 - \bar{\alpha}_{t-1}} x_0 \right)/\left( \frac{\alpha_t}{\beta_t}+\frac{1}{1 - \bar{\alpha}_{t-1}} \right)\\ &=\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}x_0+\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_t \end{aligned}, \]

\[\tilde\beta_t=1/\left( \frac{\alpha_t}{\beta_t}+\frac{1}{1 - \bar{\alpha}_{t-1}} \right)=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t \]

为了方便后续推导与论文对齐，我们将前向过程的几个高斯分布换成 DDPM 的符号：

\[\begin{aligned} q(x_t|x_{t-1})&:=\mathcal{N}(x_{t};\alpha_tx_{t-1},\beta_t\mathbb {I})\\ q(x_t|x_0)&:=\mathcal{N}(x_t;\sqrt{\bar\alpha_t}x_0, (1-\bar\alpha_t)\mathbb {I})\\ q(x_{t-1}|x_t,x_0)&=\mathcal{N}(x_{t-1};\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}x_0+\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_t,\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t\boldsymbol I)\\ \end{aligned} \]

逆向过程

\(p_\theta(x_{0:T})\) 称为逆向过程（reverse process），也就是去噪过程，这个过程也是一个马尔科夫链，开始于 \(p(x_T)=\mathcal{N}(x_T;\mathbb {0}, \boldsymbol{I})\) （\(x_T\) 是完全破坏的高斯噪声分布）：

\[p_\theta(x_{0:T}):=p(x_T)\prod^T_{t=1}p_\theta(x_{t-1}|x_t),\space\space\space p_\theta(x_{t-1}|x_t):=\mathcal{N}(x_{t-1};\mathbb{\mu}_\theta(x_t,t),\boldsymbol{\Sigma}_\theta(x_t,t)) \]

其中：

\(\boldsymbol{\mu}_\theta(x_t, t)\)是条件均值，表示在给定 \(x_t\) 和时间步 \(t\) 的情况下， \(x_{t-1}\) 的均值。
\(\boldsymbol{\Sigma}_\theta(x_t, t)\) 是条件协方差，表示在给定 \(x_t\) 和时间步 ( t ) 的情况下， \(x_{t-1}\) 的不确定性。

损失函数是最大化变分下界：

\[\mathbb{E}[-\log p_\theta(x_0)]\leq\mathbb{E}_q[-\log \frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}]=\mathbb{E}_q[-\log p(x_T)-\sum_{t\geq1}\log\frac{p_\theta(x_{t-1}|x_t)}{q(x_t|x_{t-1})}]:=L \]

也可以进一步重写成：（KL 散度会比直接梯度下降的方差更小？外层的E其实没啥必要，不知道为什么要加进来）

\[\begin{equation} L=\underbrace{D_{KL}(q(x_T|x_0)\|p(x_T))}_{L_T} + \underbrace{\Sigma_{t>1} D_{KL}(q(x_{t-1}|x_t, x_0)\|p_\theta(x_{t-1}|x_t))}_{L_{t-1}} - \underbrace{\mathbb{E}_q[\log p(x_0|x_1)]}_{L_0} \end{equation} \]

注意最后一项实际上可以视为第二项在 \(t=1\) 时的 KL 散度：

\[-\mathbb{E}_q[\log p(x_0|x_1)]=\mathbb{E}_q[\log \frac{q(x_{0}|x_1, x_0)}{p(x_0|x_1)}]=D_{KL}(q(x_{0}|x_1, x_0)\|p_\theta(x_{0}|x_1)) \]

于是这个损失实际上可以写为：

\[\begin{equation} L=D_{KL}(q(x_T|x_0)\|p(x_T)) + \sum_{t>0} D_{KL}(q(x_{t-1}|x_t, x_0)\|p_\theta(x_{t-1}|x_t)) \end{equation} \]

记各部分损失为：

\[\begin{aligned} L_T&=D_{KL}(q(x_T|x_0)\|p(x_T))\\ L_{0:T-1}&=\sum_{t>0} D_{KL}(q(x_{t-1}|x_t, x_0)\|p_\theta(x_{t-1}|x_t)) \end{aligned} \]

我们要用 KL 散度比较 \(q(x_{t-1}|x_t)\) 和 \(p_\theta(x_{t-1}|x_t)\) （马尔科夫假设），我们就还需要知道 \(q(x_{t-1}|x_t,x_0)\) 是什么。在 \(x_0\) 的条件下，后验扩散条件概率 \(q(x_{t-1}|x_t, x_0)\) 是一个高斯分布：

\[q(x_{t-1}|x_t,x_0)=\mathcal{N}(x_{t-1};\tilde{\mu}_t(x_t,x_0),\tilde{\beta}_t\mathbb {I}) \]

其中：

推导：

根据二次函数的性质，可以计算 \(x_{t-1}\) 的均值和方差：

\[\tilde\beta_t=1/\left( \frac{\alpha_t}{\beta_t}+\frac{1}{1 - \bar{\alpha}_{t-1}} \right)=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t \]

于是所有的 KL 散度到此就都是高斯分布之间的计算，因此可以用精确的闭式解计算而不是高方差的MC采样（ Rao-Blackwellized fashion ）。

从 \(x_0\) 根据分布 \(q(x_t|x_0):=\mathcal{N}(x_t;\sqrt{\bar\alpha_t}x_0, (1-\bar\alpha_t)\boldsymbol{I})\) 重参数化采样 \(x_t\) ，记采样的噪声为 \(\boldsymbol \epsilon\sim\mathcal N(0,\boldsymbol{I})\)，有：

\[x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{(1-\bar\alpha_t)}\boldsymbol \epsilon_t \]

（消元）于是我们反过来写 \(x_0\) ：

\[x_0=\frac{1}{\sqrt{\bar\alpha_t}}(x_t-\sqrt{1-\bar\alpha_t}\boldsymbol{\epsilon}_t) \]

代入 \(\tilde\mu_t\) ：

\[\tilde\mu_t(x_t,x_0)=\frac{1}{\sqrt\alpha_t}(x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\boldsymbol \epsilon_t)=\frac{1}{\sqrt\alpha_t}(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\boldsymbol \epsilon_t) \]

DDPM

回顾之前推导出的扩散模型的各部分损失：

\[\begin{aligned} L_T&=D_{KL}(q(x_T|x_0)\|p(x_T))\\ L_{0:T-1}&=\sum_{t>1} D_{KL}(q(x_{t-1}|x_t, x_0)\|p_\theta(x_{t-1}|x_t)) \end{aligned} \]

前向过程

DDPM对扩散模型进行了简化。

在原始模型中， \(\beta\) 是可以学习的参数，DDPM 设定 \(\beta_0\) 到 \(\beta_T\) 是 0 到 1 之间线性递增的常数，具体而言是 \(\beta_1=10^{-4}, \beta_T=0.02\) 。于是整个 \(q\) 没有任何学习的参数，也就是说 \(L_T\) 是个常数，不需要优化。

逆向过程

前向过程中，后验扩散概率为：

\[q(x_{t-1}|x_t,x_0)=\mathcal{N}(x_{t-1};\tilde{\mu}_t(x_t,x_0),\tilde{\beta}_t\boldsymbol{I}) \]

逆向过程中，模型每一步的预测的噪声分布为：

\[p_\theta(x_{t-1}|x_t):=\mathcal{N}(x_{t-1};\mathbb{\mu}_\theta(x_t,t),\boldsymbol{\Sigma}_\theta(x_t,t)) \]

两个高斯分布之间的 KL 散度的表达式为：

\[D_{\text{KL}}\left(\mathcal{N}(\mu_0, \sigma_0^2) \parallel \mathcal{N}(\mu_1, \sigma_1^2)\right) = \frac{1}{2} \left( \frac{\sigma_0^2}{\sigma_1^2} + \frac{(\mu_1 - \mu_0)^2}{\sigma_1^2} - 1 + \ln\left(\frac{\sigma_1^2}{\sigma_0^2}\right) \right) \]

DDPM 设定方差 \(\boldsymbol{\Sigma}_\theta(x_t,t)=\sigma_t^2\boldsymbol{I}\) 为常数，一般取 \(\sigma_t^2=\beta_t\) 或 \(\sigma_t^2=\tilde\beta_t=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t\) 于是优化的目标变成了让模型预测的均值 \(\mu_\theta(x_t,t)\) 尽可能靠近 \(\tilde\mu_t(x_t,x_0)\) ，也就是均方误差尽可能小：

\[L_{t-1}=\mathbb{E}_q\bigg[\frac{1}{2\sigma_t^2}\|\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t,\mathbf{x}_0)-\boldsymbol{\mu}_\theta(\mathbf{x}_t,t)\|^2\bigg]+C \]

结合 \(\tilde\mu_t(x_t,x_0)=\frac{1}{\sqrt\alpha_t}(x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\boldsymbol \epsilon_t)\) ，简化损失函数：

\[\begin{aligned} L_{t-1}-C =\mathbb{E}_{\mathbf{x}_0,\boldsymbol{\epsilon}}\left[\frac{1}{2\sigma_t^2}\left\|\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}\right)-\boldsymbol{\mu}_\theta(\mathbf{x}_t,t)\right\|^2\right] \end{aligned} \]

此时模型 \(\boldsymbol\mu_\theta\) 的目标就是预测 \(\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t(\mathbf{x}_0,\boldsymbol{\epsilon})-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}\right)\) 。对于模型来说， \(\boldsymbol x_t\) 是给定的，实际上模型的工作是预测 \(\boldsymbol \epsilon\) ，也就是说只有 \(\boldsymbol \epsilon\) 带有参数。于是模型可以重写为：

\[\boldsymbol{\mu}_\theta(\mathbf{x}_t,t)=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}_\theta\right) \]

于是损失函数可以进一步写为：

\[L_{t-1}-C =\mathbb{E}_{\mathbf{x}_0,\boldsymbol{\epsilon}}\left[\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)}\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta\right\|^2\right] \]

而 \(\boldsymbol{\epsilon}_\theta\) 是一个和 \(\boldsymbol x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{(1-\bar\alpha_t)}\boldsymbol \epsilon\) 以及 \(t\) 相关的函数，于是上式可以表达为：

\[\mathbb{E}_{\mathbf{x}_0,\boldsymbol{\epsilon}}\left[\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)}\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon},t)\right\|^2\right] \]

最终简化得到的变分下界损失函数为：

\[L_{\mathrm{simple}}(\theta):=\mathbb{E}_{t,\mathbf{x}_0,\boldsymbol{\epsilon}}\Big[\left\|\epsilon-\epsilon_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon},t)\right\|^2\Big], \space t=1,2,...,T \]

采样（模型推理一步）的过程为：

\[\mathbf{x}_{t-1}=\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{\theta}(\mathbf{x}_{t},t)\right)+\sigma_{t}\mathbf{z},\space where \space\boldsymbol z\sim\mathcal N(0,\mathbb {I}) \]

这个采样的过程在本质上和 score-based 模型是一样的。

为什么还要加入一点噪声呢？那是因为我们预测的噪声其实并不是我们想要的噪声，而是目标分布 \(p_\theta(x_{t-1}|x_t):=\mathcal{N}(x_{t-1};\mathbb{\mu}_\theta(x_t,t),\sigma_{t}^2)\) 的一个参数，也就是目标噪声分布的均值，实际的噪声需要进行采样才能得到最后的结果，否则生成的结果会很糟糕。

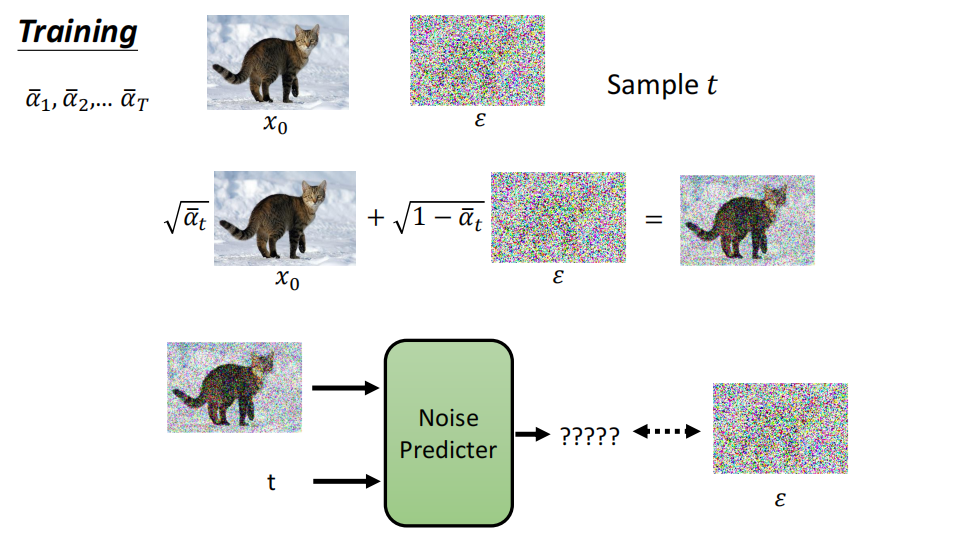
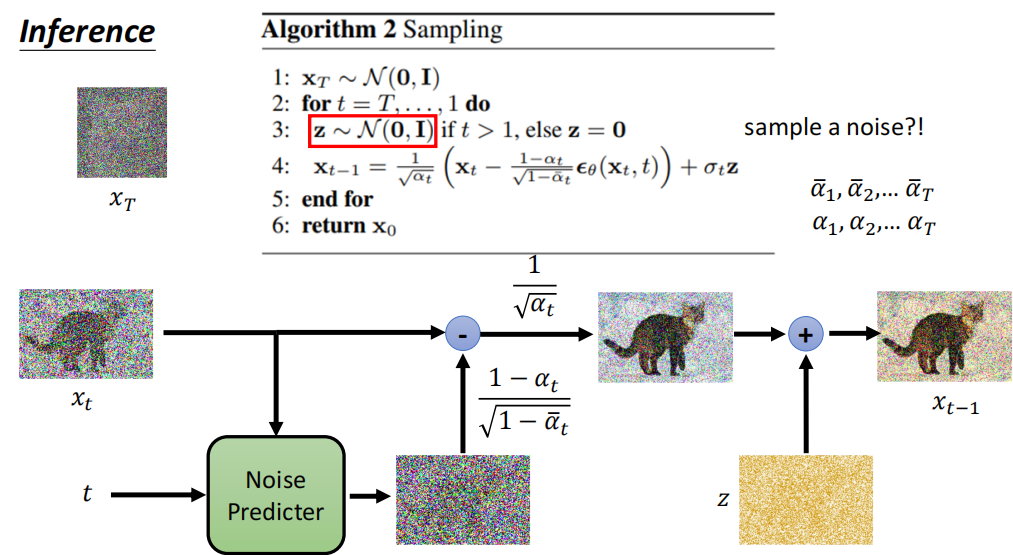
迭代的步数很多，在 DDPM 取的是 1000 步。也就是说， DDPM 最大的贡献是证明了扩散模型的实力，实际上它的内存和时间开销都是很大的。

Score-base Model

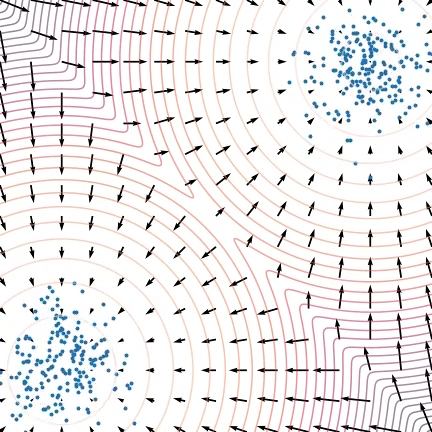
Score Methods

回顾 EBM ，我们把模型学习的数据分布定义如下：

\[P_\theta(x)=\frac{e^{-f_\theta(x)}}{Z_\theta} \]

其中配分函数 \(Z_\theta\) 很难显式地计算出来，因而成为了这类模型需要面对的困难。不过山不可过水亦可行，既然 \(Z_\theta\) 相对于 \(x\) 是个常数，那么就可以用求梯度的方式避开这个困难。

定义分数函数 \(s_\theta\) 表示数据分布对数的梯度如下：

\[\mathbf{s}_\theta(\mathbf{x})=\nabla_\mathbf{x}\log p_\theta(\mathbf{x})=-\nabla_\mathbf{x}f_\theta(\mathbf{x})-\underbrace{\nabla_\mathbf{x}\log Z_\theta}_{=0}=-\nabla_\mathbf{x}f_\theta(\mathbf{x}) \]

Annealed Langevin dynamics

简单来说就是在采样的不同步时使用不同级别的噪声（实际上就是控制噪声的方差 \(\sigma_i\) 不断递减）扰动来生成数据，这对应了 DDPM 的从噪声逐步生成数据。

郎之万动力学采样的表达式如下：

\[\boldsymbol x_{i+1}\leftarrow \boldsymbol x_i+\epsilon\nabla_{\boldsymbol x}\log p(x)+\sqrt {2\epsilon}\boldsymbol z_i,\space \space i=0,1,...,K \]

其中，\(\boldsymbol z_i\sim\mathcal N(0,\boldsymbol I)\) ，当 \(\epsilon\rightarrow0,K\rightarrow \infty\) 时就是精确采样（郎之万-蒙特卡洛理论），实际中也可以用 Metropolis-Hastings 算法来矫正误差，不过论文选择忽略这一点。可见采样是一个 MCMC 过程，不过得益于 score matching 方法，训练时并不需要完整轨迹的采样，避免了 MCMC 带来的高方差问题。

退火的想法来源于：1. 根据流形假设，真实数据是嵌入在高维空间中的低维流形，这会导致梯度在某些维度上是未定义的，在实验中，加一个极小的（肉眼不可见的）高斯噪扰动，让数据的分布在整个 \(\mathbb{R}^D\)空间中都有非零概率密度（即全支撑），就会使训练平稳很多。这是给数据添加噪声的原因。2. 低密度数据区域的问题，普通的基于分数的模型就容易在低密度 / 无密度区域因为学到了错误的分数而打转，导致收敛需要的时间变长，而这类区域往往占据了大多数区域。这是让数据初始时噪声大往后逐步减小的原因。

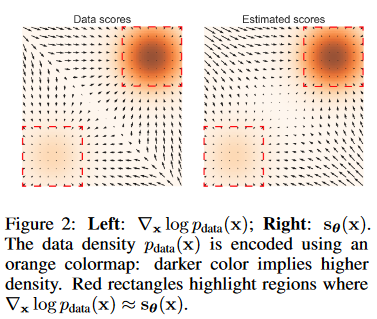
文章设定 \(\{\sigma_i\}^L_{i=1}\) 是一个正等比数列 \(\frac{\sigma_1}{\sigma_2}=\cdots=\frac{\sigma_{L-1}}{\sigma_L}>1\) 用 \(q_\sigma(\mathbf{x})\triangleq t p_{\mathrm{data}}( \mathbf{t} ) \mathcal{N} ( \mathbf{x} \mid \mathbf{t} , \sigma ^2I)dt\) 表示数据扰动，选择 \(\{\sigma_i\}_i=1^L\) ，使得 \(\sigma_1\) 足够大而 \(\sigma_L\) 足够小，目标网络需要学习一个从所有噪声数据中预测分数的联合概率分布： \(\forall\sigma\in\{\sigma_i\}_{i=1}^L:\mathbf{s_\theta}(\mathbf{x},\sigma)\approx\nabla_\mathbf{x}\log q_\sigma(\mathbf{x}).\) 其中 \(\mathbf{s_{\theta}}(\mathbf{x},\sigma)\in\mathbb{R^D}\) 与 \(\mathbf{x}\in\mathbb{R^D}\) 对应的高维空间相同，文章将 \(\mathbf{s_{\theta}}(\mathbf{x},\sigma)\) 称为噪声条件分数匹配网络 (Noise Conditional Score Network, NCSN)。下图更加直观地展示了退火的过程。

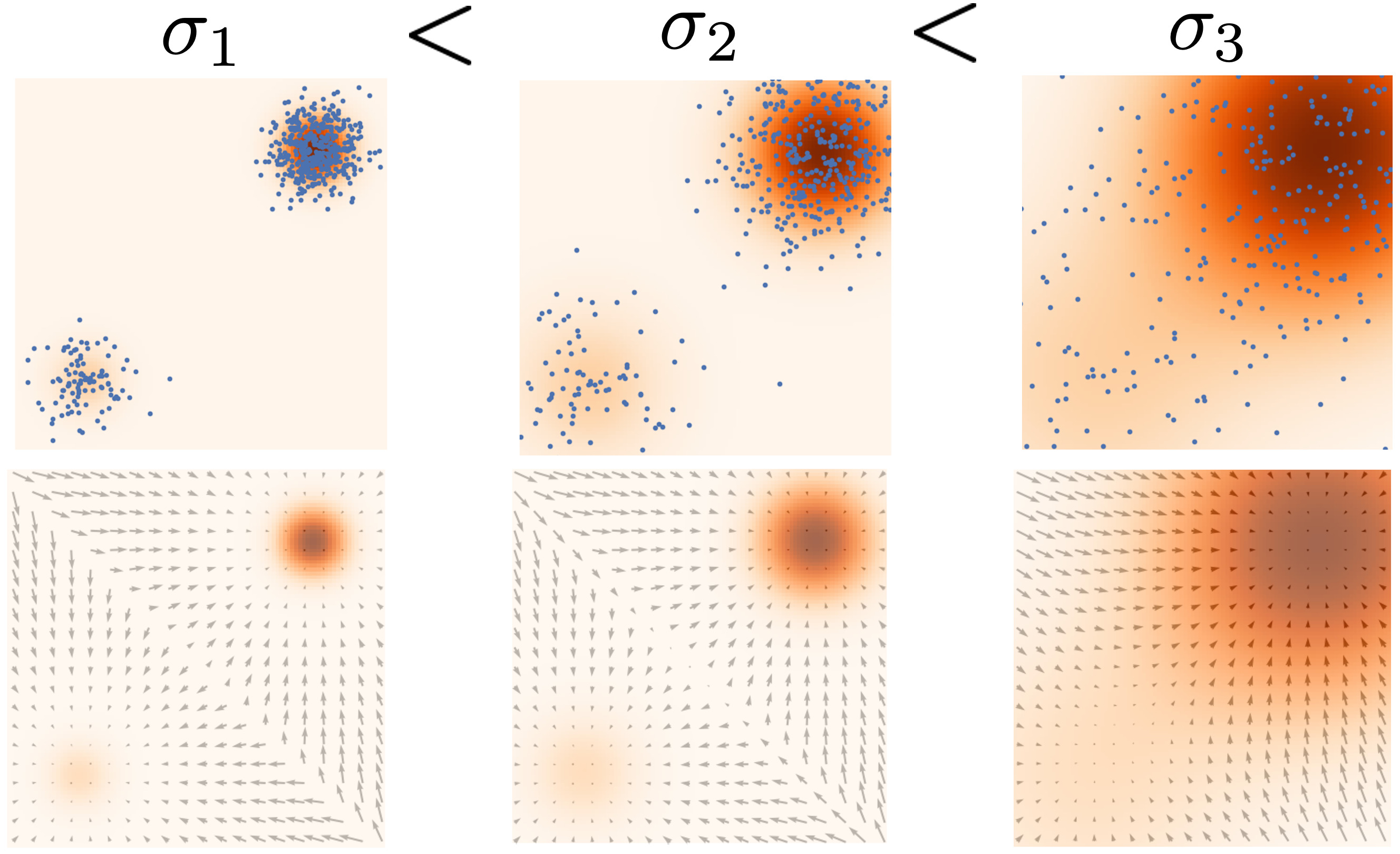
完整的采样算法如下：

Score Matching

分数匹配是在不知道真实 score 的情况下优化 score 的方法，从而避开了 MCMC 带来的高方差。

Denoising Score Matching (DSM)

Denoising Score Matching的目标是通过引入噪声并在带噪声的数据上训练评分函数，使得模型能够估计原始数据的评分函数。损失函数定义如下：

\[L=\frac{1}{2}\mathbb E_{q_\sigma(\tilde {\boldsymbol x}|\boldsymbol x)p_{data}(\boldsymbol x)}\left[ || s_\theta(\tilde {\boldsymbol x})-\nabla_{\tilde {\boldsymbol x}}\log q_\sigma(\tilde {\boldsymbol x}|\boldsymbol x) ||^2_2\right] \]

具体解释如下：

\(\tilde {\boldsymbol x}\) 和 \(\boldsymbol x\)：\(\boldsymbol x\)是从真实数据分布\(p_{data}(\boldsymbol x)\)中采样的数据点，而\(\tilde {\boldsymbol x}\)是通过对\(\boldsymbol x\)加噪声生成的。
\(s_\theta(\tilde {\boldsymbol x})\)：模型的评分函数，参数为 \(\theta\)，它尝试去估计\(\tilde {\boldsymbol x}\)的评分，即数据的概率密度梯度。
\(\nabla_{\tilde {\boldsymbol x}}\log q_\sigma(\tilde {\boldsymbol x}|\boldsymbol x)\)：这个是对数密度在 \(\boldsymbol x\) 处的真实评分（梯度）。
损失函数的含义：损失函数计算了模型评分\(s_\theta(\tilde {\boldsymbol x})\)和真实评分\(\nabla_{\tilde {\boldsymbol x}}\log q_\sigma(\tilde {\boldsymbol x}|\boldsymbol x)\)之间的均方误差。通过最小化这个损失，模型学习去逼近真实的评分函数。

Sliced Score Matching (SSM)

Sliced Score Matching 通过引入随机方向来降低计算复杂度，并在这些方向上进行评分匹配。损失函数定义如下：

\[L=\mathbb E_{p_v}\mathbb E_{p_{data}(\boldsymbol x)}\left[ \boldsymbol v^{\boldsymbol T}\nabla_{\boldsymbol x}s_\theta(\boldsymbol x)\boldsymbol v+ \frac{1}{2}|| s_\theta({\boldsymbol x}) ||^2_2\right] \]

具体解释如下：

\(p_v\)：一个简单方向分布，通常是均匀分布在单位球面上的分布，比如多元正态分布，\(\boldsymbol v\)是从这个分布中采样的随机方向向量。
\(\nabla_{\boldsymbol x}s_\theta(\boldsymbol x)\)：模型评分函数\(s_\theta(\boldsymbol x)\)对\(\boldsymbol x\)的梯度。
\(\boldsymbol v^{\boldsymbol T}\nabla_{\boldsymbol x}s_\theta(\boldsymbol x)\boldsymbol v\)：表示在方向\(\boldsymbol v\)上的评分函数梯度。这实际上是一个一维的投影，使得计算复杂度从高维空间降到一维空间。这一部分可以采用前向模式自动微分来计算，与去噪模型 DSM 不同的是，SSM 计算时从原始未扰动数据分布直接估计，需要差不多4倍的计算量。
\(\frac{1}{2}|| s_\theta({\boldsymbol x}) ||^2_2\)：评分函数的二范数平方，作为正则项。
损失函数的含义：损失函数包括两部分：第一部分是方向\(\boldsymbol v\)上的评分函数梯度的期望，第二部分是评分函数的二范数平方。通过最小化这个损失，模型学习在不同方向上的评分函数梯度，从而估计数据分布的评分函数。

总结

Denoising Score Matching：通过引入噪声并在带噪声的数据上训练模型，使得模型能估计原始数据的评分函数。
Sliced Score Matching：通过引入随机方向，降低计算复杂度，并在这些方向上进行评分匹配，使得模型能在不同方向上估计评分函数梯度。

文章采用DSM，因为训练更快速，可以看出这个式子和 DDPM 的损失是一致的。论文设置噪声分布为一个高斯分布 \(q_\sigma(\tilde {\boldsymbol x}|\boldsymbol x) \sim\mathcal N(\tilde {\boldsymbol x};\boldsymbol x,\sigma^2\boldsymbol I)\) ，于是根据高斯分布的定义有：

\[\nabla_{\tilde{\mathbf{x}}}\log q_{\sigma}(\tilde{\mathbf{x}}\mid\mathbf{x})=-(\tilde{\mathbf{x}}-\mathbf{x})/\sigma^{2} \]

对于给定的 \(\sigma\) ，带入前面的损失公式：

\[\ell(\boldsymbol{\theta};\sigma)\triangleq\frac12\mathbb{E}_{p_{daa}(\mathbf{x})}\mathbb{E}_{\tilde{\mathbf{x}}\sim\mathcal{N}(\mathbf{x},\sigma^2I)}\bigg[\left\|\mathbf{s}_{\boldsymbol{\theta}}(\tilde{\mathbf{x}},\sigma)+\frac{\tilde{\mathbf{x}}-\mathbf{x}}{\sigma^2}\right\|_2^2\bigg] \]

对于所有的 \(\sigma_i\) ，整个损失公式写为：

\[\mathcal{L}(\boldsymbol{\theta};\{\sigma_i\}_{i=1}^L)\triangleq\frac1L\sum_{i=1}^L\lambda(\sigma_i)\ell(\boldsymbol{\theta};\sigma_i), \]

其中 \(\lambda\) 用来约束不同级别的噪声对应的损失函数都有相同数量级，论文根据经验选择 \(\lambda(\sigma)=\sigma^2\) 。

SDE视角

如图所示，扩散的前向和逆向过程都可以由随机微分方程表示。

前向：

\[\mathrm{d}\mathbf{x}=\mathbf{f}(\mathbf{x},t)\mathrm{d}t+g(t)\mathrm{d}{\mathbf{w}} \]

逆向：

\[\mathrm{d}\mathbf{x}=[\mathbf{f}(\mathbf{x},t)-g(t)^2\nabla_\mathbf{x}\log p_t(\mathbf{x})]\mathrm{d}t+g(t)\mathrm{d}\bar{\mathbf{w}} \]

其中 \(\bar{\mathbf{w}}\) 是标准维纳过程从 \(T\) 到 \(0\) 的逆过程，\(\nabla_\mathbf{x}\log p_t(\mathbf{x})\) 就是我们要估计的分数。

优化目标：

\[\boldsymbol{\theta}^*=\arg\min_{\boldsymbol{\theta}}\mathbb{E}_t\Big\{\lambda(t)\mathbb{E}_{\mathbf{x}(0)}\mathbb{E}_{\mathbf{x}(t)|\mathbf{x}(0)}\Big[\left\|\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}(t),t)-\nabla_{\mathbf{x}(t)}\log p_{0t}(\mathbf{x}(t)\mid\mathbf{x}(0))\right\|_2^2\Big]\Big\} \]

常微分方程：

\[\mathrm{d}\mathbf{x}=\left[\mathbf{f}(\mathbf{x},t)-\frac{1}{2}g(t)^{2}\nabla_{\mathbf{x}}\log p_{t}(\mathbf{x})\right]\mathrm{d}t \]

小结

改进方向

这些改进或多或少都是工（lian）程（dan），主打一个百花齐放百家争鸣八仙过海各显神通，而其基本的数学理论并没有很大的革新，所以按综述概述，仅对DDIM算法细讲。

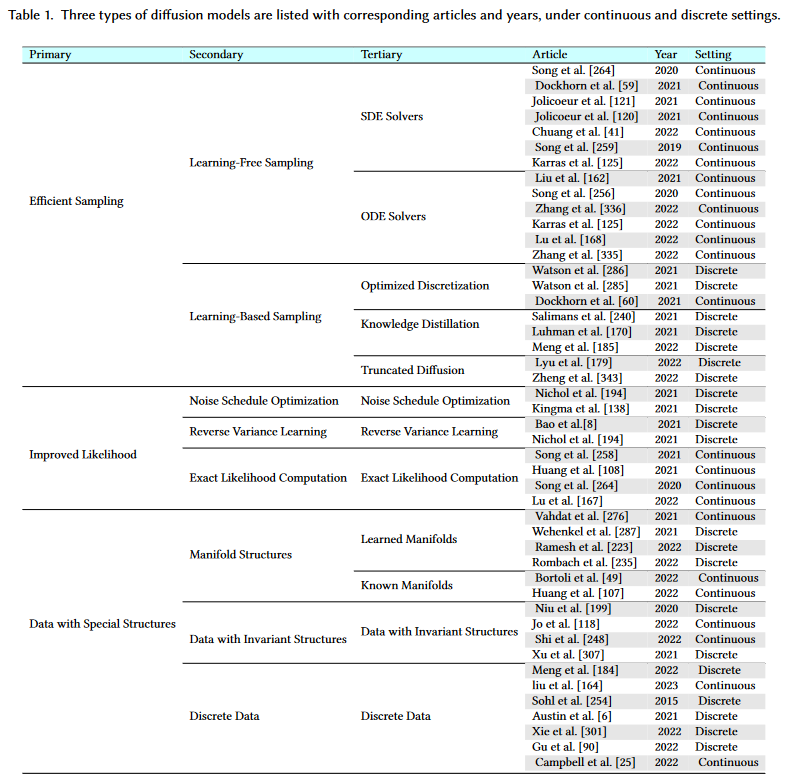
采样改进

扩散模型的训练和采样过程高度解耦，这些采样改进方案都可以直接用在 DDPM 模型上。

采样过程即是推理的过程，分为 Learning-Free 和 Learning-Based 两类。其中前者分为 DDIM 为代表的简化常微分方程（ODE）以及简化随机微分方程（SDE）；而后者通常有截断、蒸馏等方法，其效果和 DDIM 差不多（损失性能换取速度的提升），一般会学习选择的子序列或者直接训练一个新的采样器。

DDIM

根据之前推导过的公式，前向过程中每一步加噪过程都无需用马尔科夫链实现，仅需依赖 \(\boldsymbol x_0\) ，反过来采样（后向）过程也可以无需依赖马尔科夫链。

回顾之前 DDPM 的前向过程：

\[\begin{aligned} q(x_t|x_{t-1})&:=\mathcal{N}(x_{t};\alpha_tx_{t-1},\beta_t\boldsymbol{I})\\ q(x_t|x_0)&:=\mathcal{N}(x_t;\sqrt{\bar\alpha_t}x_0, (1-\bar\alpha_t)\boldsymbol{I})\\ q(x_{t-1}|x_t,x_0)&=\mathcal{N}(x_{t-1};\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}x_0+\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_t,\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t\boldsymbol I)\\ \end{aligned} \]

非马前向构造

DDIM 构造了一种非马尔科夫前向加噪过程，其中超参数 \(\sigma\in \mathbb R^T_{\geq 0}\) ：

\[q_\sigma(\boldsymbol{x}_{1:T}|\boldsymbol{x}_0):=q_\sigma(\boldsymbol{x}_T|\boldsymbol{x}_0)\prod_{t=2}^Tq_\sigma(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0) \]

其中 \(q_\sigma(x_T|x_0):=\mathcal{N}(x_t;\sqrt{\alpha_T}x_0, (1-\alpha_T)\boldsymbol{I})\) ，并且对所有 \(t>1\) 有：

\[q_\sigma(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0)=\mathcal{N}\left(\sqrt{\alpha_{t-1}}\boldsymbol{x}_0+\sqrt{1-\alpha_{t-1}-\sigma_t^2}\cdot\frac{\boldsymbol{x}_t-\sqrt{\alpha_t}\boldsymbol{x}_0}{\sqrt{1-\alpha_t}},\sigma_t^2I\right) \]

上述构造式其实是基于 \(P(x_{t-1}|x_{t},x_{0})\sim \mathcal N(kx_{0}+mx_{t},\sigma^{2}\boldsymbol I)， x_{t-1}=kx_0+mx_t+\sigma\epsilon,\epsilon\sim \mathcal N(0,\boldsymbol I)\) 的假设，用待定系数法解出来的。

为使这种构造下仍然无需改变 DDPM 的训练过程，构造式在中间时间步需要满足与 DDPM 的边缘分布一致，也就是 \(q_\sigma(x_t|x_0):=\mathcal{N}(x_t;\sqrt{\alpha_t}x_0, (1-\alpha_t)\boldsymbol{I})\) ，证明过程（翻译自论文附录B Lemma 1）：

由于 \(q_\sigma(x_t|x_0):=\mathcal{N}(x_t;\sqrt{\alpha_t}x_0, (1-\alpha_t)\boldsymbol{I})\) 在 \(t=T\) 时成立，我们要进一步证明对任一 \(t\) 成立，只需证明当 \(q_\sigma(x_t|x_0):=\mathcal{N}(x_t;\sqrt{\alpha_t}x_0, (1-\alpha_t)\boldsymbol{I})\) 成立时，\(q_\sigma(x_{t-1}|x_0):=\mathcal{N}(x_t;\sqrt{\alpha_{t-1}}x_0, (1-\alpha_{t-1})\boldsymbol{I})\) 也成立。

首先我们有：

\[q_\sigma(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0):=\int_{\boldsymbol{x}_t}q_\sigma(\boldsymbol{x}_t|\boldsymbol{x}_0)q_\sigma(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0)\mathrm{d}\boldsymbol{x}_t \]

以及：

\[q_{\sigma}(\boldsymbol{x}_{t}|\boldsymbol{x}_{0})=\mathcal{N}(\sqrt{\alpha_{t}}\boldsymbol{x}_{0},(1-\alpha_{t})\boldsymbol{I}) \]

\[q_{\sigma}(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t},\boldsymbol{x}_{0})=\mathcal{N}\left(\sqrt{\alpha_{t-1}}\boldsymbol{x}_{0}+\sqrt{1-\alpha_{t-1}-\sigma_{t}^{2}}\cdot\frac{\boldsymbol{x}_{t}-\sqrt{\alpha_{t}}\boldsymbol{x}_{0}}{\sqrt{1-\alpha_{t}}},\sigma_{t}^{2}\boldsymbol{I}\right) \]

根据高斯分布的性质，两个高斯分布相乘还是高斯分布，也就是 \(q_\sigma(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)\sim\mathcal N(\mu_{t-1},\Sigma_{t-1}\boldsymbol I)\)，其中：

\[\begin{aligned} \mu_{t-1} &=\sqrt{\alpha_{t-1}}x_{0}+\sqrt{1-\alpha_{t-1}-\sigma_{t}^{2}}\cdot\frac{\sqrt{\alpha_{t}}x_{0}-\sqrt{\alpha_{t}}x_{0}}{\sqrt{1-\alpha_{t}}} \\ &=\sqrt{\alpha_{t-1}}x_0 \ \end{aligned} \]

\[\Sigma_{t-1}=\sigma_t^2\boldsymbol{I}+\frac{1-\alpha_{t-1}-\sigma_t^2}{1-\alpha_t}(1-\alpha_t)\boldsymbol{I}=(1-\alpha_{t-1})\boldsymbol{I} \]

证毕。

确定性采样

根据 \(x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{(1-\bar\alpha_t)}\boldsymbol \epsilon_t\) ，定义从 \(x_t\) 预测 \(\epsilon_t\) 的函数：

\[f_\theta^{(t)}(\boldsymbol{x}_t):=(\boldsymbol{x}_t-\sqrt{1-\alpha_t}\cdot\epsilon_\theta^{(t)}(\boldsymbol{x}_t))/\sqrt{\alpha_t} \]

那么生成过程就是（用 \(f\) 替代 \(x_0\)）：

\[p_\theta^{(t)}(x_{t-1}|x_t)=\begin{cases}\mathcal{N}(f_\theta^{(1)}(x_1),\sigma_1^2\boldsymbol{I})&\text{if }t=1\\q_\sigma(x_{t-1}|x_t,f_\theta^{(t)}(x_t))&\text{otherwise}\end{cases} \]

也就是说当 \(t=1:T\) 时，生成过程写为：

\[x_{t-1}=\sqrt{\alpha_{t-1}}\underbrace{\left(\frac{x_t-\sqrt{1-\alpha_t}\epsilon_\theta^{(t)}(x_t)}{\sqrt{\alpha_t}}\right)}_{\text{“predicted }\boldsymbol{x}_0\text{”}}+\underbrace{\sqrt{1-\alpha_{t-1}-\sigma_t^2}\cdot\epsilon_\theta^{(t)}(x_t)}_{\text{“direction pointing to }\boldsymbol{x}_t\text{”}}+\underbrace{\sigma_t\epsilon_t}_{\text{random noise}} \]

当 \(\sigma_t^2=\tilde\beta_t=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t\) 时，DDIM 与 DDPM 等价；当 \(\sigma_t^2=0\) 时，整个过程是一个确定性采样，这就是 DDIM。

respacing 加速采样

取一个 \(1,...,T\) 上长度为 \(S\) 的子序列 \(\tau\) 上进行采样，损失一定精度换来速度的提升。

生成过程为：

\[p_\theta(\boldsymbol{x}_{0:T}):=\underbrace{p_\theta(\boldsymbol{x}_T)\prod_{i=1}^Sp_\theta^{(\tau_i)}(\boldsymbol{x}_{\tau_{i-1}}|\boldsymbol{x}_{\tau_i})}_{\text{use to produce samples}}\times\underbrace{\prod_{t\in\overline{\tau}}p_\theta^{(\iota)}(\boldsymbol{x}_0|\boldsymbol{x}_t)}_{\text{in variational objective}} \]

其中：

\[p_{\theta}^{(\tau_{i})}(x_{\tau_{i-1}}|x_{\tau_{i}})=q_{\sigma,\tau}(x_{\tau_{i-1}}|x_{\tau_{i}},f_{\theta}^{(\tau_{i})}(x_{\tau_{i-1}}))\quad\mathrm{if}\space i\in[S],i>1\\p_{\theta}^{(t)}(\boldsymbol{x}_{0}|\boldsymbol{x}_{t})=\mathcal{N}(f_{\theta}^{(t)}(\boldsymbol{x}_{t}),\sigma_{t}^{2}\boldsymbol{I})\quad\mathrm{otherwise} \]

小结

其实从 DDPM 的训练看，模型学的就是 \(1,...,T\) 上的一个子集，DDIM 的实质质就是牺牲多样性（不确定性）换时间。

另外， DDIM 是在优化 ODE 求解的典型方法。

蒸馏方法

渐进式蒸馏

在 DDIM 的基础上学一些跨步的生成器，最后把步数减少到 4 步。训练过程与 DDPM 基本相同。

Consistency Models

这篇还是宋飏的文章，被 ICML2023 接收，论文称一步采样即可达到很好的效果，唯一的缺点是我看不懂（）。

Consistency Models (arxiv.org)

定义一致性函数 \(\boldsymbol f(\cdot , \cdot)\) 满足边界条件 \(\boldsymbol f(\boldsymbol x_\epsilon, \epsilon)=\boldsymbol x_\epsilon\) ，文章采用跳跃连接的方式进行参数化：

\[f_{\boldsymbol{\theta}}(\mathbf{x},t)=c_{\mathrm{skip}}(t)\mathbf{x}+c_{\mathrm{out}}(t)F_{\boldsymbol{\theta}}(\mathbf{x},t) \]

其中 \(c_{\mathrm{skip}}(\epsilon)=1\) 且 \(c_{\mathrm{out}}(\epsilon)=0\) ， \(f\) 在 \(t=\epsilon\) 时可微。

采样：

训练可以还是蒸馏 DDPM ，也可以从头训练。

似然估计改进

这方面的工作通常有优化噪声调度，也就是优化设定的噪声方差表；另一类就是将之前 DDPM 里固定的方差 \(\Sigma_\theta\) 纳入考虑范围；还有一种是直接优化 ODE 方程求似然估计的精确解。

离散扩散模型

D3PM：其实最主要的就是泛化定义了加噪去噪的过程，将噪声用 [MASK] 来进行替代。

LDM

让 Diffusion 出圈的是 Stable Diffusion （CVPR 2022），它首次提出了 LDM ，通过用隐藏层进行扩散优化了训练和推理的成本，这一点在很大程度上参考了 VQ-GAN，同时将模型扩展为条件生成。综述将它归类到“学习的流形数据”之下，应该是认为隐空间是一种“流形数据”。

LCM-lora 是清华 2023 年的一个工作，将步数减少到 1~4 步且没有很多损失，同时 LoRA 的权重可以直接插入微调后的 LDM 中，应用时不同风格的模型可以直接叠加而不用重新训练，在网络上反响很大（但好像被 ICLR 2024 拒了），效果展示在：Latent Consistency Models: Synthesizing High-Resolution Images with Few-step Inference (latent-consistency-models.github.io)