切蛋糕（叉积）

​
**

题目*

*：
有一个圆形蛋糕，圆心座标为(xc,yc),半径为R。座标系中有一些草莓。现在要沿圆心切出半个蛋糕，使得包含草莓最多。落在蛋糕边界上也算是包含。

样例解释：

第一个样例最优解：

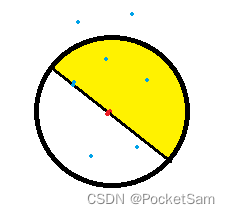
第二个样例最优解：

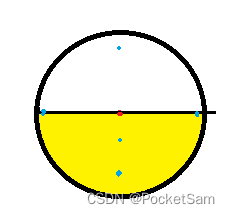
输入格式

单组测试数据。 第一行有三个浮点数，分别表示xc，yc，R。 第二行有一个整数n（1<=n<=200），表示草莓的数目。 接下来n行，每一行两个浮点数，表示草莓的座标xi,yi。 所有草莓的座标不一样，以上所有浮点数都在0到2000之间。

输出格式

输出一个整数，表示最多能包含的草莓的数目。

输入样例

样例输入1
25 25 3.5
7
25 28
23 27
27 27
24 23
26 23
24 29
26 29
样例输入2
350 200 2.0
5
350 202
350 199
350 198
348 200
352 200

输出样例

样例输出1
3
样例输出2
4

分析

：
数据范围比较小，时间上不用太担心超时

本题有两个关键：
1.判断点是否在圆内，可用勾股定理判断；
2.判断半圆内的点的个数，根据离散化的思想，最优解半圆的直边上一定存在一个草莓
所以遍历每个点，作点和圆心的连线，求出一边的点的个数，取最大值就是答案
在这里就需要叉积；
即若有两个点（x1，y1），（x2，y2）
k=(x1y2)-(x2y1);若k>0,则逆时针旋转；k<0，则为顺时针；k=0，则旋转180度或0度

​题解：

#include<bits/stdc++.h>
using namespace std;
double xc,yc,r;
int n;
double q,p;
struct si{
	double x,y;
}s[210];
int cnt;
int MAX=0;
int main(){
	scanf("%lf%lf%lf",&xc,&yc,&r);
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%lf%lf",&q,&p);
		if(r*r>=(q-xc)*(q-xc)+(p-yc)*(p-yc)){
			cnt++;
			s[cnt].x=q;
			s[cnt].y=p;
		}
	}
	for(int i=1;i<=cnt;i++){
		int sum1=0,sum2=0;
		int xb=s[i].x-xc;
		int yb=s[i].y-yc;
		for(int j=1;j<=cnt;j++){
			int xd=s[j].x-xc;
			int yd=s[j].y-yc;
			if(xb*yd-yb*xd>0){
				sum1++;
			}
			else if(xb*yd-yb*xd<0){
				sum2++;
			}
			else{
				sum1++;
				sum2++;
			}
		}
		int ans=max(sum1,sum2);
		if(ans>MAX){
			MAX=ans;
		}
	}
	cout<<MAX;
}

**

sum up：

**666666