#最短路#

前言：

最短路的算法主要有4种：Dijkstra,Spfa,Bellman-ford,Floyd

本文将一一介绍

---

引入题目：

【模板】单源最短路径（标准版） - 洛谷（数据卡spfa与bellman-ford）

【模板】单源最短路径（弱化版） - 洛谷
 

【模板】Floyd 算法 - 洛谷（练练手吧，实际上用dijkstra更快）

---

Dijkstra:

dijkstra算法核心就是贪心，用一张图说明：

如果我们想从1-->6走最短路

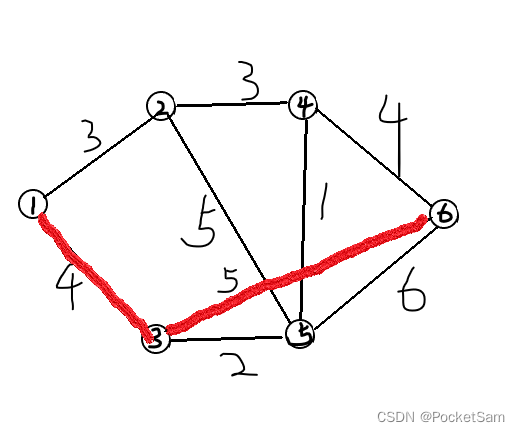
我们开始访问1节点，将所有与1连接的节点找出，并计算出到它们的路程，更新最小路程；将这两个信息存入优先队列（按路程大小排序）并标记1节点；之后不断从优先队列中取出节点，更新最小路；

最后我们就可以求出从1节点到所有点的最短路；

解决引入题目的代码（dijkstra版）献上：
 

#include<bits/stdc++.h> 
#define N 100005
using namespace std;
int n,m,s;
int head[N];
int cnt;
int dis[N];
bool vis[N];
struct edge{
	int next,to,w;
}e[N<<2];//N*4
struct st{
	int pos,dis;
};
struct cmp{//按路程升序排序 
	bool operator ()(st x, st y) {
        return x.dis>y.dis;
    }
};
priority_queue<st,vector<st>,cmp >q; 

void add(int from,int to,int w){//运用邻接表储存边的信息 
	e[++cnt].next=head[from];
	e[cnt].to=to;
	e[cnt].w=w;
	head[from]=cnt;
}
void dijkstra(int k){
	q.push((st){k,0}) ;
	while(!q.empty()){
		int u=q.top().pos;
		q.pop();
		if(vis[u])continue;
		vis[u]=1;//进行标记，不再查询此点 
		for(int i=head[u];i;i=e[i].next){
			int v=e[i].to;
			if(dis[v]>dis[u]+e[i].w){
				dis[v]=dis[u]+e[i].w;//更新最短路 
				if(!vis[v]){
					q.push((st){v,dis[v]});
				} 
			}
		}
	}
}
int main() {
	scanf("%d %d %d",&n,&m,&s);
	for(int i=1;i<=m;i++){
		int u,v,w;
		scanf("%d %d %d",&u,&v,&w);
		add(u,v,w);
	}
	memset(dis,0x3f3f3f3f,sizeof(dis));//赋极大值 ，方便取min 
	dis[s]=0;
	dijkstra(s);
	for(int i=1;i<=n;i++){
		printf("%d ",dis[i]);
	}
}

dijkstra的优点就在于它是比较快的，时间复杂度较为优秀；

但它无法处理带负边的最短路问题

---

Spfa:

spfa算法写法上与dijkstra相近，但其可解决带负边的问题

献上代码

#include<bits/stdc++.h>
const int maxn=100005;
const int maxm=500005;
using namespace std;
int n,m,s,cnt=0;
int dis[maxn];
int head[maxm];
bool vis[maxn];
struct Edge{
  	int next,to,w;
}e[maxm]; //结构体表示静态邻接表
void add(int from,int to,int w){ //邻接表建图
  	e[++cnt].next=head[from]; //链式存储下一条出边
  	e[cnt].to=to; //当前节点编号
  	e[cnt].w=w; //本条边的距离
  	head[from]=cnt; //记录下一次的出边情况
}
void spfa(){
  	queue<int> q; //spfa用队列，这里用了STL的标准队列
  	for(int i=1;i<=n;i++){
  		dis[i]=2147483647;	
	}
  	q.push(s); dis[s]=0; vis[s]=1; //第一个顶点入队，进行标记
  	while(!q.empty()){
    	int u=q.front(); //取出队首
    	q.pop(),vis[u]=0;
    	for(int i=head[u];i;i=e[i].next){
    		int v=e[i].to;
    		if(dis[v]>dis[u]+e[i].w){
    			dis[v]=dis[u]+e[i].w;
    			if(!vis[u]){
    				q.push(v),vis[v]=1;
				}
			}
		}
  	}
}
int main(){
  	cin>>n>>m>>s;
  	for(int i=1; i<=m; i++){
    	int u,v,w;
    	cin>>u>>v>>w; 
    	add(u,v,w); //建图，有向图连一次边就可以了
  	}
  	spfa(); //开始跑spfa
  	for(int i=1; i<=n; i++)
    	if(s==i) cout<<0<<" "; //如果是回到自己，直接输出0
    	else cout<<dis[i]<<" "; //否则打印最短距离
}

spfa容易被卡数据，导致T掉，所以慎用

---

Bellman-ford:

在这里，因为此算法较为生疏，详细分析一下：

初始源点的dis为0，其余皆为无限大（即赋极大值），

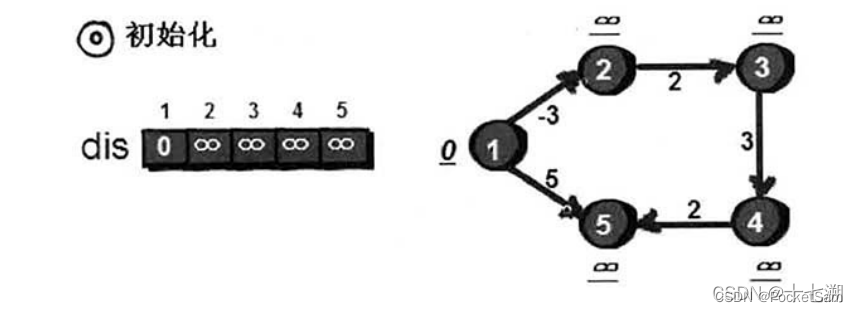
第一轮松弛：

开始枚举2-->3这条边，欲用dis[2]与此边的边权w更新dis[3],但发现dis[2]+w>dis[3],无法得到更短的路径，故不更新；

接着枚举1--2这条边，发现dis[1]+w(如图可知w==-3)<dis[2]，就更新dis[2]=dis[1]+w;

之后依次枚举，重复以上判断即可完成第一轮松弛；得到如下图的dis;

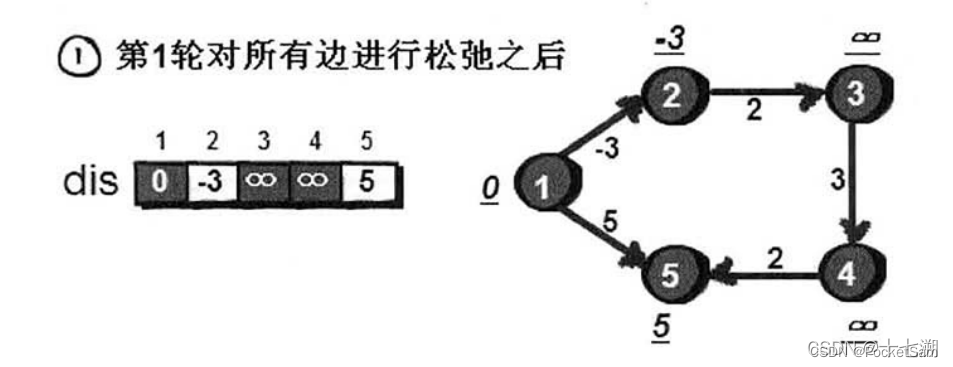
 接着进行第二轮松弛：

枚举2-->3这条边时就会发现dis[2]+w<dis[3],这时我们就可以更新dis[3]的值了；

这样枚举完所有边我就可以得到更多的dis,如下图：

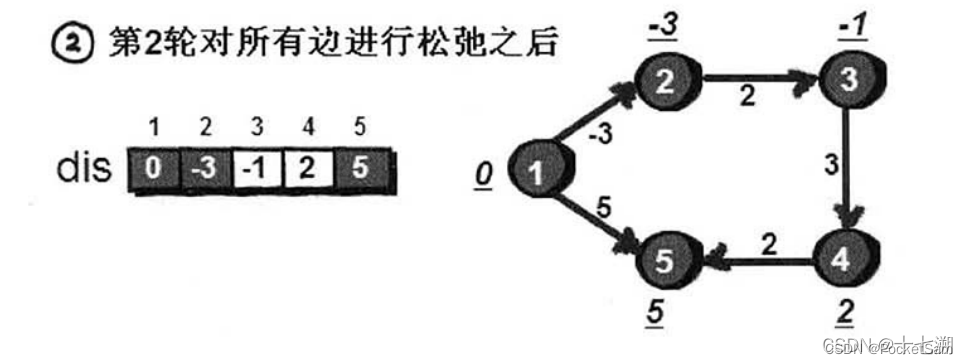
 具体代码实现奉上：

#include<bits/stdc++.h>
#define N 100005
using namespace std;
int n,m,s,cnt;
int dis[N];
struct edge{
	int u,v,w;
}e[N<<3];
void add(int from,int to,int w){
	e[++cnt].u=from;
	e[cnt].v=to;
	e[cnt].w=w;
}
void bellmanford(int k){
	dis[k]=0;
	for(int i=1;i<=n-1;i++){
		for(int j=1;j<=m;j++){
			int u=e[j].u,v=e[j].v,w=e[j].w;
			if(dis[u]!=2147483647&&dis[v]>dis[u]+w){
				dis[v]=dis[u]+w;
			}
		}
	}
}
int main (){
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;i++){
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);
	}
	for(int i=1;i<=n;i++) dis[i]=2147483647;
	bellmanford(s);
	for(int i=1;i<=n;i++){
		printf("%d ",dis[i]);
	}
} 

说真的bellman-ford的时间复杂度太不行了，但可以找负环，

并有特殊的用法：上面的迭代次数是有实际意义的，比如我们迭代了k次，那么我们求的最短距离就是从1号点经过不超过k条边走到n号点的最短距离。

---

Floyd:

【模板】Floyd 算法 - 洛谷

Floyd比较暴力，时间复杂度为O(),并不推荐，但在就全源最短路时还有点用处

直接上代码：

#include <bits/stdc++.h>
#define maxn 105
using namespace std;
int dis[maxn][maxn];
int n, m;
void Floyd(){
	for(int k=1; k<=n; k++) // 中间点
		for(int i=1; i<=n; i++) // 起始点
			for(int j=1; j<=n; j++) // 终点
			{
				int d = dis[i][k] + dis[k][j]; // i->k->j
				if(d < dis[i][j]) dis[i][j] = d; // 取最短长度
			}
}
int main(){
	scanf("%d%d", &n, &m);
	// 初始化，注意初始值不能超过INT_MAX/2（防止两个INF相加溢出）
	memset(dis, 0x3f, sizeof (dis)); 
	// 每个点到自己的距离为0
	for(int i=1; i<=n; i++)
		dis[i][i] = 0;
	// 读入边
	while(m--)
	{
		int u, v, d;
		scanf("%d%d%d", &u, &v, &d);
		u, v; // 0-index
		dis[u][v] = dis[v][u] = d; // 注意两个值都要设
	}
	Floyd();
	for(int i=1; i<=n; i++, putchar('\n'))
		for(int j=1; j<=n; j++)
			printf("%d ", dis[i][j]);
	return 0;
}

云也终有出岫之时