BZ周赛Round#2
目录
A.robot
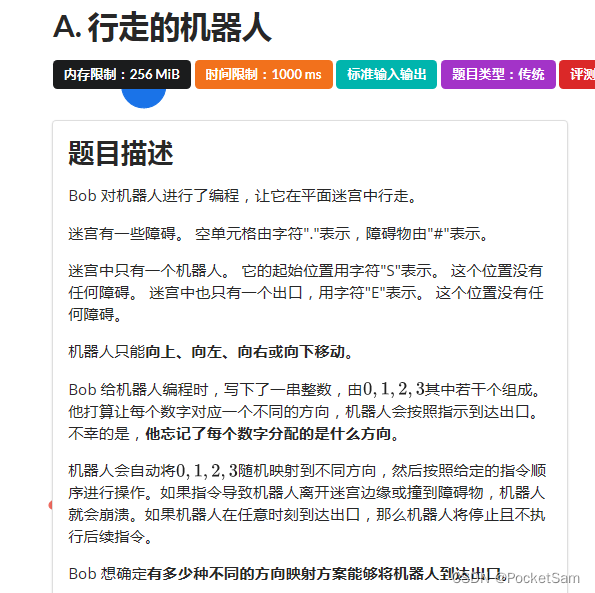
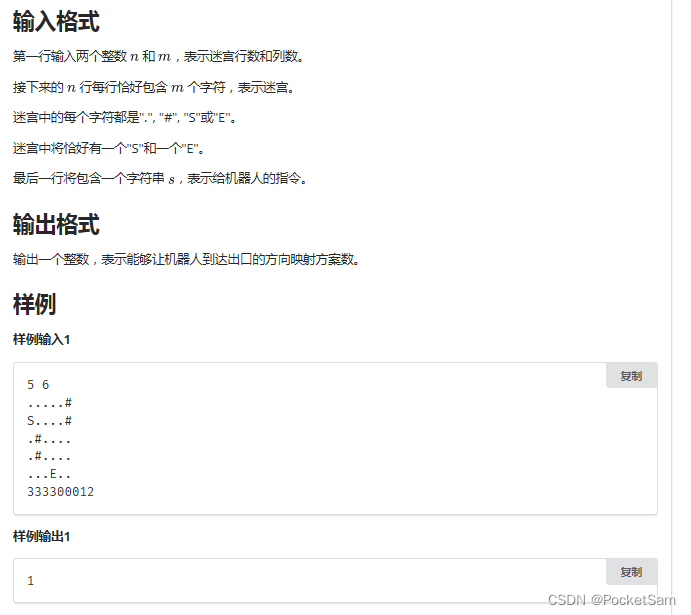
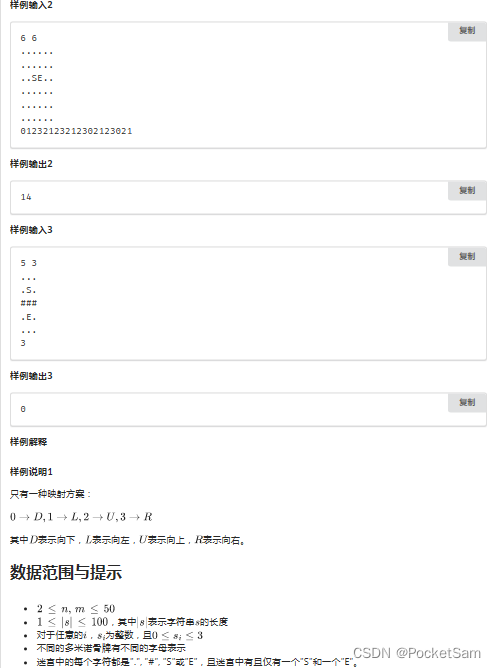
估算一下，一共小于4^4种，dfs直接爆搜
code:
cnt的特判注意一下为cnt>=len+1
#include<bits/stdc++.h>
#define xp first
#define yp second
using namespace std;
int n,m,len,ans;
pair<int,int>s;
char a[105][105];
string b;
bool check(int i,int j,int k,int l){
if(i==j||i==k||i==l||j==k||j==l||k==l) return 1;
return 0;
}
void dfs(int x,int y,int i,int j,int k,int l,int cnt){
if(x<1||x>n||y<1||y>m||cnt>=len+1||a[x][y]=='#') return;
if(a[x][y]=='E') {
ans++;
return;
}
if(b[cnt]=='0'){
if(i==0) dfs(x,y-1,i,j,k,l,cnt+1);
else if(i==1) dfs(x,y+1,i,j,k,l,cnt+1);
else if(i==2) dfs(x-1,y,i,j,k,l,cnt+1);
else dfs(x+1,y,i,j,k,l,cnt+1);
}
else if(b[cnt]=='1'){
if(j==0) dfs(x,y-1,i,j,k,l,cnt+1);
else if(j==1) dfs(x,y+1,i,j,k,l,cnt+1);
else if(j==2) dfs(x-1,y,i,j,k,l,cnt+1);
else dfs(x+1,y,i,j,k,l,cnt+1);
}
else if(b[cnt]=='2'){
if(k==0) dfs(x,y-1,i,j,k,l,cnt+1);
else if(k==1) dfs(x,y+1,i,j,k,l,cnt+1);
else if(k==2) dfs(x-1,y,i,j,k,l,cnt+1);
else dfs(x+1,y,i,j,k,l,cnt+1);
}
else{
if(l==0) dfs(x,y-1,i,j,k,l,cnt+1);
else if(l==1) dfs(x,y+1,i,j,k,l,cnt+1);
else if(l==2) dfs(x-1,y,i,j,k,l,cnt+1);
else dfs(x+1,y,i,j,k,l,cnt+1);
}
}
int main(){
//freopen("robot.in","r",stdin);
//freopen("robot.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
if(a[i][j]=='S') s=make_pair(i,j);
}
}
cin>>b;
len=b.size();
for(int i=0;i<4;i++){
for(int j=0;j<4;j++){
for(int k=0;k<4;k++){
for(int l=0;l<4;l++){
if(check(i,j,k,l)) continue;
dfs(s.xp,s.yp,i,j,k,l,0);
}
}
}
}
printf("%d",ans);
}B.paint
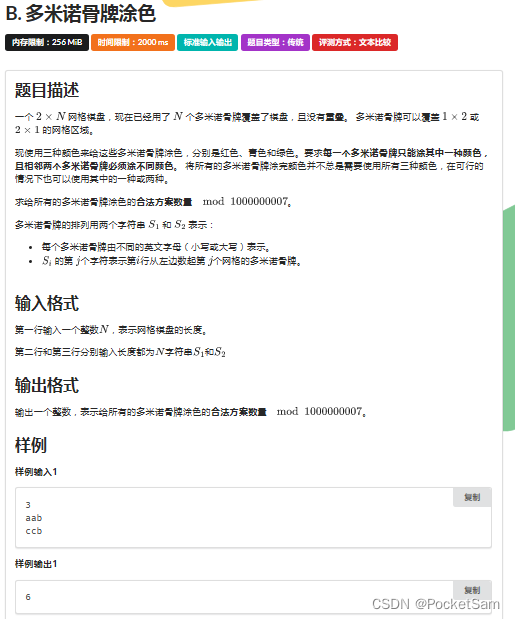
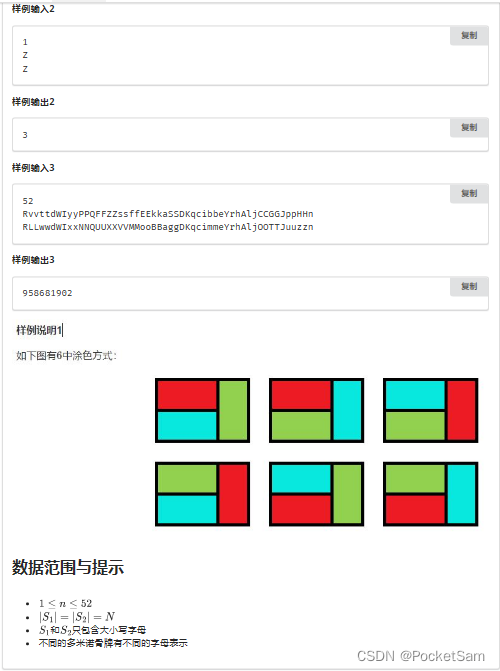
瞪眼法观察，发现可以使用乘法原理进行答案的求解：
case1：当前是一个竖着放的骨牌，又分两种情况
case1.1 前面也是一个竖着放的骨牌：因为前面已有一个确定的颜色，所以当前位·· 置只有两种颜色可选，故ans*=2
case1.2 前面是两个横着放的骨牌：因为前面已有两个确定的颜色，所以当前位·· 置只有一种颜色可选，故ans不变、
case2:当前是两个横着放的骨牌，同理分两种情况讨论
case2.1 前面是一个竖着放的骨牌: 对于两个横着放的骨牌其中一个确定颜色加上 前面是一个竖着放的骨牌，另一个即可确定， 故ans*=2
case2.2 前面是两个横着放的骨牌:画图统计发现，ans*=3;
code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
int n;
ll ans=1;
char a[3][60];
int main(){
//freopen("paint.in","r",stdin);
//freopen("paint.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=2;i++)
for(int j=1;j<=n;j++)
cin>>a[i][j];
for(int j=1;j<=n;j++){
if(j==1){
if(a[1][j]==a[2][j]) ans*=3;
else{
ans*=6;
j++;
}
}
else {
if(a[1][j-1]==a[2][j-1]){
if(a[1][j]==a[2][j]) ans=(ans<<1)%mod;
else{
ans=(ans<<1)%mod;
j++;
}
}
else {
if(a[1][j]==a[2][j]) continue;
else{
ans=(ans*3)%mod;
j++;
}
}
}
}
printf("%lld",ans%mod);
}C.mex
是否注意到，答案总是不超过 2？
第一步，考虑能否使答案为 0，这就意味着不存在两个0 相邻，也就是说只要 0的数量不超过n/2(上取整)就行；
第二步，考虑能否使答案为 1，注意此时已有条件 的数量超过 ，那么不能让 0和 1相邻，如果本就不存在ai=1，或是存在某个数ai=x>1，构造如下排列[0,0,......0,x,1,1......,1]就能使答案为1；
最后，对于剩下只含0 和1 的数组，因为 0的数量超过n/2，构造排列 ，使答案为 2.
code:
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,T;
int x;
int sum;
bool f;
int main(){
scanf("%d",&T);
while(T--){
f=0,sum=0;
scanf("%d",&n);
for(int i=1;i<=n;i++) {
scanf("%d",&x);
if(x==0) sum++;
if(x>1) f=1;
}
if(sum==n) printf("1\n");
else if(sum>int(n/2.0+0.999999)){
if(f) printf("1\n");
else printf("2\n");
}
else printf("0\n");
}
}D.luckey:
欧拉定理板题：
欧拉定理：如果gcd(a,p)==1,那么
code:
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
int cnt;
ll L;
ll gcd(ll x,ll y){return y?gcd(y,x%y):x;}
ll oula(ll m){
ll w=m;
for(int i=2;i*i<=m;i++){
if(m%i==0){
w-=w/i;
while(m%i==0)m/=i;
}
}
if(m>1)w-=w/m;
return w;
}
ll pow_mod(__int128 x , __int128 n , __int128 mod ){
__int128 ans = 1;
__int128 t = x % mod ;
while(n) {
if(n & 1){
ans =(ans*t)%mod;
}
t = (t*t)%mod;
n >>= 1 ;
}
return ans ;
}
int main () {
while(scanf("%lld",&L)&&L){
ll m=9*L/gcd(L,8);
printf("Case %d: ",++cnt);
if(gcd(m,10)==1){
ll num=oula(m);
ll sum=num;
for(ll i=1;i*i<=num;i++){
if(num%i==0){
if( pow_mod (10 , i , m)== 1) {
sum=min(sum, i);
break;
}
if( pow_mod(10 , num/i ,m)== 1) sum=min(sum, num/i);
}
}
printf("%lld\n",sum);
}
else printf("0\n");
}
}E.grafun:
为了方便理解，我们需要一些符号：
bound(x,y)表示按照题目描述的方式断开顶点 x和 y的所有路径时，最后删除的那条边。
例如，图中 bound(2,6)=edge(2,6)
f(u,v)表示有序顶点对(x,y)的数量，满足bound(x,y)=edge(u,v)
例如 f(2,6)=4，因为bound(1,3),bound(1,6),bound(2,3),bound(2,6)
均等于
edge(2,6)
w(u,v)
表示
edge(u,v)
的权值
csum(u,v)
表示权值不大于
w(u,v)
的权值前缀和。
csum(u,v)
容易计算，按照边权排序后可求出前缀和。
考虑一条边
(u,v)
对答案的贡献。按照题目描述的过程，在删除这条边之前，所有权值比它小的边均已经删
除。总共删除的边权之和为
csum(u,v)
。
总计有
f(u,v)
数量的点对是以边
(u,v)
作为最后一条删除的边的。因此边
(u,v)
对答案的贡献为：
f(u,v) * csum(u,v)
对所有的边求出贡献之和，即为最终的答案。
如果高效求出一条边
(u,v)
的
f(u,v)
呢？
整个过程类似于
Kruskal
算法的执行过程。
假定初始时图中包含所有的点，但没有边。我们按照边权从大到小的顺序加入每条边。设在加入一条边
(u,v)
时，顶点
u
和
v
所属的连通块的顶点数分别为
c1, c2
，则
f(u, v) = c1 * c2
。
证明：因为按照边权从大到小的顺序加边，那么在加入边（
u, v)
之前，顶点
u
和
v
所属的连通块的边权均大于
edge(u, v)
。那么在按照题目描述方式删边时，当删除到
edge(u,v)
时，顶点
u
和
v
所属的连通块必须保持连
通，块内的边均尚未删除。且这时的连通块是极大的。
两个连通块之间的点对满足
bound(x, y)=edge(u,v)
。
而每个连通块内部的点对满足：bound(
,
)!=edge(u,v)
故有：f(u,v)=c1*c2
code:
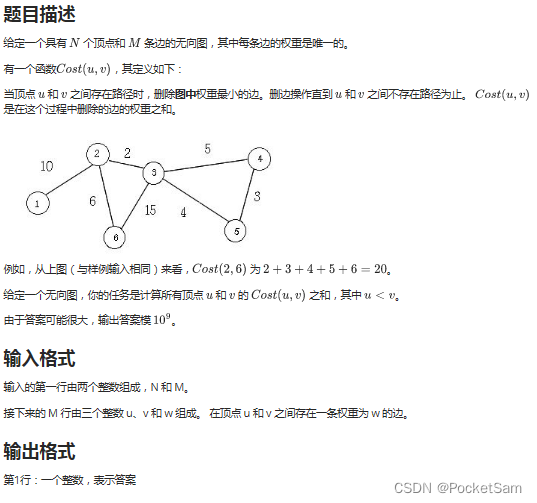
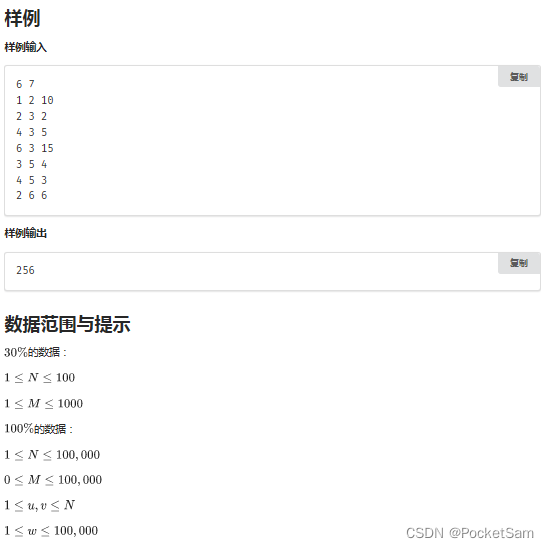
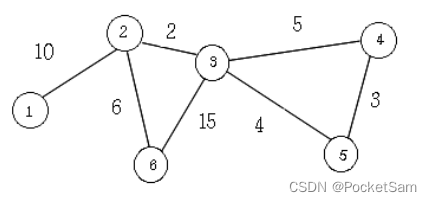
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100005;
const ll mod=1e9;
int n,m;
ll ans;
int fa[N];
ll sz[N],cost[N];
struct edge{
int u,v;
ll w;
}e[N];
bool cmp(edge a,edge b){return a.w>b.w;}
int find(int k){
if(k==fa[k]) return k;
else fa[k]=find(fa[k]);
return fa[k];
}
ll unite(int a,int b){
int ra=find(a),rb=find(b);
if(ra==rb) return 0;
else{
ll res=sz[ra]*sz[rb];
fa[ra]=rb;
sz[rb]+=sz[ra];
return res;
}
}
void kruskal(){
for(int i=1;i<=m;i++){
if(find(e[i].u)==find(e[i].v)) continue;
ans+=unite(e[i].u,e[i].v)*cost[i]%mod;
}
}
int main () {
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++) scanf("%d%d%lld",&e[i].u,&e[i].v,&e[i].w);
for(int i=1;i<=n;i++) fa[i]=i,sz[i]=1;
sort(e+1,e+1+m,cmp);
for(int i=m;i>0;i--) cost[i]=e[i].w+cost[i+1];
kruskal();
printf("%lld\n",ans%mod);
}F.subset:
样例：
输入：
41
71
3
5
50
75
2
19
47
88
95
92
110
111
117
58
124
130
57
129
168
161
29
39
206
79
10
142
107
209
210
222
221
223
242
104
264
265
202
279
314
315
输出：
22
奇数一边，偶数一边，求二分图的最小独立子集
code：
#include<bits/stdc++.h>
#define fi first
#define se second
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int N=505;
int n,res,cb,cc;
ll a[N],b[N],c[N];
bool e[N][N],vis[N];
int ff[N];
int cnl,cnr,cx[N],cy[N];
ll gcd(ll x,ll y) {return y?gcd(y,x%y):x;}
int path(int u){
int v;
for(v=0;v<cnr;v++){
if(e[u][v]&&!vis[v]){
vis[v]=1;
if(cy[v]==-1||path(cy[v])){
cx[u]=v;
cy[v]=u;
return 1;
}
}
}
return 0;
}
int main(){
//freopen("subset.in","r",stdin);
//freopen("subset.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) {
scanf("%lld",&a[i]);
if(a[i]&1) b[++cb]=i;
else c[++cc]=i;
}
memset(ff,-1,sizeof ff);
for(int i=1;i<=cb;i++){
bool f=0;
for(int j=1;j<=cc;j++){
if(gcd(a[b[i]],a[c[j]])==1&&gcd(a[b[i]]+1,a[c[j]]+1)==1){
f=1;
if(ff[j]==-1) {
ff[j]=cnr;
e[cnl][cnr++]=1;
}
else{
e[cnl][ff[j]]=1;
}
}
}
if(f) cnl++;
}
memset(cx,-1,sizeof cx);
memset(cy,-1,sizeof cy);
for(int i=0;i<cnl;i++){
if(cx[i]==-1){
memset(vis,0,sizeof vis);
res+=path(i);
}
}
printf("%d\n",n-res);
}qwq,只考了202pts,悲
本文来自博客园，作者：MegaSam，转载请注明原文链接：https://www.cnblogs.com/MegaSamTXL/p/17607134.html
浙公网安备 33010602011771号