Constructive Algorithms!
Constructive Algorithms!
前言
构造题,顾名思义,就是有 constructive algorithms 标签的题目。它们往往给出某些若干限制,并要求选手构造出符合这些限制的对象,例如序列、图和树等。当然,对于某些交互题,构造具体的询问策略也可以视作一类构造题。甚至,一道带输出方案的数据结构题也可能是构造题。这类题目往往不好用某一类特定算法来解决,只能对具体问题具体分析。
然而,尽管题与题之间最终算法 / 构造出的方案差距很大,这类题目还是有一些基本的技法和分析技巧。本篇挑选了一些有代表性的题目,旨在展示面对在各种风格迥异的题目的时候,一些可能有效的分析方法,以及一些可能可参考的,逐步得到可行解的思考路径。
可能有用的方法
如果直接在方法处插入对应例题就有点奇怪:这样提示就太明显了。
所以这一节是一些不结合题目的纸上谈兵。请仔细体会。
方法零:简单尝试
很多选手的注意力相当集中。他们往往可以直接观察到一组解,然后通过;或是尝试一些简单策略,然后通过。如果一个题短时间内通过了非常多人,那么就可以试试枚举简单策略。
方法一:精细构造
对于一些题目,构造的限制可能比较严格。但是,我们可以相对容易地得到离限制较为接近的一组解。这个时候,重新审视构造这组解的过程,我们可能发现某一些部分可以更优,从而,对这一组解微调就可以得到满足限制的解。
例如:
- 递归到小范围的时候,可以直接使用搜索得出的最优解,而不是人工构造的可行解;
- 交互题的询问进行到某个阶段的时候,可以复用一部分之前得出的信息;
- 构造进行到某个阶段的时候,当前局面的性质已经比初始时更好,从而可以换用常数更小的操作方法继续构造。
方法二:打表 (小范围搜索)
对于限制越少的题目,打表的用武之地就越大。一般来说,题目的输入量越少(例如只有一个 \(n\)),构造的自由度就越大。这个时候,解的组数会很多,最优解 / 最小字典序解通常也会具有某种规律。观察出这些规律,就有较大概率通过题目。
例如:
- 直接搜索得出 \(n\) 较小时的一组解,然后推广到一般情况;
- 搜索得出有解的情况,只针对有解情况进行人工构造,避免虚空做题;
- 搜索一些特殊局面下的解,试图获得启发,然后推广到一般情况。
当然,打表并非要依赖输入量少这一性质。部分题目中,尽管输入规模可能达到 \(O(n)\) 级别,但是稍加分析,可以发现,大部分输入都不如特定的某组极限数据强。这个时候,如果能打表得出极限数据的规律,那么稍加微调自然可以解决更弱的输入。
然而,打表也不是万能的。有的时候简单的可行解不是最优解 / 最小字典序解,而是混在解集中,难以辨认。另外,对于部分题目,随着 \(n\) 的增长,搜索范围可能会迅速增大(譬如:搜索的时间复杂度是 \(O((n!)^2)\) 或者 \(O(2^{n^2})\)),从而使得搜索运行时间无法接受。
方法三:从解的形式出发
这里包含两类方法:
-
考虑有解的条件。
对于可能会区分有 / 无解的题目,如果暂且不明确哪些情况会无解,可以先思考一些无解的充分条件。这些充分条件可以排除掉一些情况,使得关于剩下的情况的构造更为简明。如果能证明剩下的情况都可以被构造出来那么就解决了。
例如:\(n\) 是奇 / 偶数的时候无解,由此延伸出各种处理方法:将 \((2i-1,2i)\) 配对构造,或者 \((i,i+n/2)\) 配对构造,等等。
-
考虑解具体是什么。
一类最优化问题通常是,让你构造出一组最优解,但是这个最优值具体是多少还不明了。可以考虑先找出这个最优值,再根据这个最优值的形式进行具体构造。
方法四:强化题目限制
和方法一中那些需要精细构造的题目不同,很多时候题目的自由度太高,解集太大,反而导致无从下手。我们可以自行强化题目限制,缩小解集大小,从而可以结合上人工构造 / 打表等一系列操作。
涉及到不同对象的时候,强化的方法也有区别。这里没有什么好的概括。
方法五:归纳构造
没什么好的办法的时候可以试试归纳。这样只需要考虑如何从 \(n \to n+k\) 或 \(n \to n - k\),比直接构造整个解要好一些。
当然有的时候肯定不能满足于 \(n \to n + k\),还要结合上 \(n \to kn\) 的操作(通常出现在若干次 \(O(\log n)\) 次构造出 \(n\) 这样的题目里面)。
例如:
- 给当前局面设计一个势能,然后找到一组操作,使得在操作之后这个局面的势能减少。只要对于每个局面都设计这样一组操作就可以了。
- 人工构造 / 搜索出小范围的解,然后找到若干组支持 \(n \to n + k\)(\(n \to kn\))的操作。组合这些操作得到答案。
方法六:构造基本操作
有的时候,题目中给出的可用的操作非常奇怪,不符合我们的认知习惯。这个时候可以尝试组合题中的可用操作,得到符合我们认知习惯的基本操作,然后在擅长的领域内解决问题。
例如:组合操作得出循环移位 / 交换 / 给某个位置减少 \(1\),然后利用组合后的操作解决问题。
方法七:随机化 / 乱搞
实在做不出来的时候也可以试试这个,构造的自由度越高,效果越好,有的时候可能有奇效。
Part 0. 热身题
这一部分题目不需要很多前面提到的方法。在一定时间的尝试之后我们便可以得到一组看上去正确的解,对这组解微调就可以通过。当然,微调也许是困难的。
AGC052A Long Common Subsequence
题解
我们发现构造出长度等于 \(2n\) 的 LCS 非常简单,可以猜测长度为 \(2n+1\) 的 LCS 也不太困难。
一种合理的猜测是,感觉构造和这个 \(3\) 有点关系,因为 \(2^2 - 3 = 1\),说不定只给出 \(3\) 个串就是干这个用的呢?
但事实上没有关系,因为我们是有通解的。简单枚举之后发现:输出 \(n\) 个 \(1\),然后 \(n\) 个 \(0\),然后一个 \(1\) 即可通过。这也没什么办法,构造总是需要多多尝试。
证明:若 \(S\) 中最后一个位置是 \(1\),那么在 \(S+S\) 的前 \(n\) 个字符中取出 \(n\) 个 \(1\),中间 \(n-1\) 个字符中取出 \(n\) 个 \(0\),最后一个字符固定为 \(1\);否则,设 \(S\) 中极长全 \(0\) 后缀长度为 \(k\),那么在 \(S+S\) 的前 \(n\) 个字符中取出 \(n\) 个 \(1\) 和 \(k\) 个 \(0\);而我们只需要在后 \(n\) 个字符中取出前 \(n-k\) 个 \(0\),因为这是极长连续段,所以取完第 \(n-k\) 个 \(0\) 之后后面必然还剩下至少一个 \(1\)。
Codeforces 1227G Not Same
题解
题目可以转化为:在 \((n+1) \times n\) 的网格内填 \(0/1\),使得第 \(i\) 列的和恰好为 \(a_i\),且每一行互不相同。
考虑 \(a_i\) 全部为 \(n\) 的时候我们有简单策略,也就是:第 \(i\) 列从第 \(i\) 行开始填 \(n\) 个 \(1\),填出去了就从第 \(1\) 行开始继续填。
简单尝试发现:当 \(a_i\) 降序排序的时候,采用类似的方法,第 \(i\) 列从第 \(i\) 行开始填 \(a_i\) 个 \(1\)。
证明留作习题。
习题解答
反证法。不妨设第 \(i\) 行和第 \(j\) 行 \((i<j)\) 完全相同。
如果 \(j \leq n\),考虑 \((i,i+1)\) 的值,它必须为 \(0\),因为 \(a_{i+1} \leq n\)。根据假设,\((j,i+1)\) 也必须为 \(0\),那么就导出 \(a_{i+1} \leq j-i-1\)。因为 \(a_{i+2} \leq a_{i+1}\),从而 \((i,i+2)\) 和 \((j,i+2)\) 必须全部为 \(0\),这样就得出了 \(a_{i+2} \leq j-i-2\)。反复运用会得到 \(a_{j} \leq 1\),而按照填数规则和假设,\((j,j)\) 和 \((i,j)\) 必须全部为 \(1\),这导出 \(a_j \geq 2\),从而矛盾。
如果 \(j = n+1\),我们容易得出 \(a_1 < i\)。运用类似的分析,同样容易推出矛盾。
代码
# include <bits/stdc++.h>
const int N=1010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n,a[N];
int p[N];
int v[N][N];
inline int cmp(int x,int y){
return a[x]>a[y];
}
int main(void){
n=read();
for(int i=1;i<=n;++i) a[i]=read(),p[i]=i;
std::sort(p+1,p+1+n,cmp);
for(int l=1;l<=n;++l){
for(int d=1,x=l;d<=a[p[l]];++d,x=x%(n+1)+1){
v[x][p[l]]=1;
}
}
printf("%d\n",n+1);
for(int i=1;i<=n+1;++i,puts("")) for(int j=1;j<=n;++j) printf("%d",v[i][j]);
return 0;
}
AGC030C Coloring Torus
题解
题意中给出的四个位置即为该位置行列循环意义下的邻居。
当 \(k \leq 500\) 的时候直接第 \(i\) 列填 \(i\) 即可通过。注意到 \(k \leq 1000\),这启发我们构造不会太复杂,可以直接在这种填法上面微调。
简单尝试后发现,某个位置的邻居在斜线上是相邻的。这启发我们把构造旋转 \(45\) 度,改为第 \(i\) 条对角线填上 \(i\)。我们可以很自然地发现第 \(i\) 条对角线交错填 \(i\) 和 \(i+500\) 是可行的,于是我们解决了 \(k = 1000\) 的情形。对于 \(500 < k < 1000\) 的情况是类似的,具体来说,如果 \(i+ 500 \leq k\) 就交错填 \(i\) 和 \(i + 500\),否则直接填 \(i\) 即可。
代码
# include <bits/stdc++.h>
const int N=505,INF=0x3f3f3f3f,V=500;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int k;
int v[N][N];
int main(void){
k=read();
if(k<=V){
printf("%d\n",k);
for(int i=1;i<=k;++i) for(int j=1;j<=k;++j){
printf("%d%c",i," \n"[j==k]);
}
return 0;
}else{
int n=V;
printf("%d\n",n),k-=n;
for(int i=1;i<=n;++i){
for(int x=1,y=i;x<=n;++x,y=(y==1?n:y-1)){
v[x][y]=(i<=k?(x&1)*n+i:i);
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j) printf("%d ",v[i][j]);
puts("");
}
}
return 0;
}
Codeforces 1896G Pepe Racing
题解
本题乍一看无从下手。不妨考虑子问题:如何询问得出这 \(n^2\) 个数的最大值编号?
我们可以用 \(n+1\) 次询问得到答案。具体地,我们给这 \(n^2\) 个人分为 \(n\) 组,查询组内的最大值编号,然后查询这 \(n\) 组的最大值编号。
现在,考虑下一个问题:如何询问得出次大值编号?
虽然最大值所在组已经不足 \(n\) 人,但是,我们还是可以用 \(n\) 次询问覆盖到所有的 \(n^2-1\) 个人,最后再查询一次。以此类推,可以发现,总查询次数为惊人的 \(O(n^3)\)。
我们发现,询问次大值时,对于之前信息的利用不够。只有最大值所在组的最大值编号会改变。而对于其它组,最大值编号是不变的。现在问题在于如何求出最大值所在组的最大值编号。
一个直接的想法是,直接拼一个其它组的元素。这是不可行的,就算该元素在自己的组内比较小,也有可能直接比最大值所在组的剩下 \(n-1\) 个元素都大。但是,当我们重新审视「分组」这一操作的时候,我们发现,这一轮的分组并不需要和上一轮保持一致。因此,我们可以采用以下策略:直接拼一个其它组的,不是所在组最大值的元素到当前组,然后查询。如果该元素是最大值,就直接将这个元素划分到当前组,并成为当前组的最大值。
这一流程显然是可以继续推广的。当剩余元素数量大于 \(2n-1\) 的时候,我们采用以下策略:
- 将每个组的最大值编号拼到一次查询中,得到目前的最大值编号。
- 从最大值编号所在组中删除该元素。此时,该组可能会被删空。因为剩余元素数量大于 \(2n-1\),因此至少有 \(n\) 个元素没有成为所在组的最大值。我们总是可以将这些元素的若干个,和该组剩余元素,拼成一次询问,然后重新得到该组的最大值。这一过程可能会更改元素的分组。
这样,任意时刻每组都有至少一个元素。
当剩余元素数量等于 \(2n-1\) 的时候,情况有一些不一样:现在在执行上面策略的第二步时,凑不齐 \(n\) 个元素进行一组询问了。我们注意到,现在只剩下 \(n-1\) 个没有成为所在组最大值的元素,但是总共也只剩下 \(2n-1\) 个元素。合理猜测剩下的 \(n-1\) 个元素恰好是前 \(n-1\) 小。这也是容易证明的:
- 当一个元素成为组内最大值的时候,它必然不是前 \(n-1\) 小。
- 现在剩下 \(2n-1\) 个元素,我们已知其中 \(n\) 个元素不是前 \(n-1\) 小,那么剩下的 \(n-1\) 个元素必然是前 \(n-1\) 小。
于是这一部分可以采用以下方法解决:
- 如果只剩下一个不是前 \(n-1\) 小的元素,则它是第 \(n\) 小,不需要任何询问。
- 否则,取出场上所有不是前 \(n-1\) 小的元素,然后拼上若干个前 \(n-1\) 小组成一次询问,询问的答案就是剩余元素最大值。然后删去该元素。
考虑总询问次数:
- 询问最大值:共 \(n+1\) 次。
- 询问中间的 \((n^2-1)-(2n-1)\) 个数:共 \(2(n^2-2n)\) 次。
- 询问最后 \(n\) 个数:共 \(n\) 次。
这样,我们的总询问次数恰好为 \(2n^2 - 2n + 1\) 次,可以通过此题。
代码
# include <bits/stdc++.h>
const int N=405,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int a[N];
int n;
typedef std::vector <int> poly;
inline int query(poly &c){
assert((int)c.size()==n);
printf("? "); for(auto v:c) printf("%d ",v); puts(""); fflush(stdout);
return read();
}
std::set <int> mn,s[N];
int bel[N],mx[N];
std::vector <int> ans;
inline void remove(int x){
ans.push_back(x);
for(int i=1;i<=n;++i) if(i!=bel[x]&&s[i].size()){
int v=*s[i].begin();
s[bel[x]].insert(v),bel[v]=bel[x],s[i].erase(v);
break;
}
std::vector <int> b;
for(auto v:s[bel[x]]) b.push_back(v);
if((int)b.size()<n) for(auto v:mn){
if(bel[v]!=bel[x]) b.push_back(v);
if((int)b.size()==n) break;
}
int id=query(b);
mx[bel[x]]=id;
if(bel[id]!=bel[x]) s[bel[id]].erase(id),s[bel[id]=bel[x]].insert(id);
mn.erase(mx[bel[x]]),s[bel[x]].erase(mx[bel[x]]);
return;
}
std::mt19937 rng(time(0));
inline void solve(void){
n=read(); mn.clear(),ans.clear();
poly b;
for(int k=1;k<=n;++k){
s[k].clear();
poly w;
for(int x=(k-1)*n+1;x<=k*n;++x) w.push_back(x),bel[x]=k;
b.push_back(mx[k]=query(w));
for(int x=(k-1)*n+1;x<=k*n;++x) if(x!=mx[k]) mn.insert(x),s[k].insert(x);
}
remove(query(b));
for(int x=n*n-1;x>2*n-1;--x){
poly w;
for(int k=1;k<=n;++k) w.push_back(mx[k]);
remove(query(w));
}
std::set <int> r;
for(int k=1;k<=n;++k) r.insert(mx[k]);
while(r.size()>1){
poly w; for(auto v:r) w.push_back(v);
if((int)w.size()<n) for(auto v:mn){
w.push_back(v); if((int)w.size()==n) break;
}
int cmx=query(w); r.erase(cmx), ans.push_back(cmx);
}
ans.push_back(*r.begin());
printf("! ");
for(auto v:ans) printf("%d ",v); puts(""); fflush(stdout);
return;
}
int main(void){
int T=read();
while(T--) solve();
return 0;
}
Part 1. 从解的形式出发
这一部分的题一般要先考虑解的形式,再具体构造。
QOJ 5434 Binary Substrings
题解
(From Sol1)
枚举每一个长度 \(l\),长度为 \(l\) 的本质不同子串个数有两个上界:\(2^l\) 和 \(n−l+1\)。
直接加起来可以得到答案的显然上界:
\[\sum \limits_{i=1}^n \min\{2^l,n-l+1\} \]
当然,具体构造仍然是不太简单的。
我们感性理解,如果长度为 \(k\) 的 \(01\) 串出现了 \(2^k\) 个,那么长度为 \(k' < k\) 的 \(01\) 串肯定也全出现了。同时,如果长度为 \(k\) 的所有 \(n-k+1\) 个子串都是不同的,那么长度为 \(k' > k\) 的 \(01\) 串肯定也全部不同。
找到最大的 \(k\) 使得 \(2^k \leq n-k+1\),此时,如果长度为 \(k\) 的 \(01\) 串全部出现过,长度为 \(k+1\) 的子串都是不同的,那么每一部分都取满上界。
考虑图论模型。构造有 \(2^k\) 个点的图 \(G_k\)。图上的所有点恰好代表每一种长度为 \(k\) 的 \(01\) 串。若串 \(s\) 去掉首字符,并加上串 \(t\) 的末字符恰好就是串 \(t\),则连边 \(s \to t\)。不难发现,每个点有两条入边两条出边,图中共 \(2^{k+1}\) 条边,恰好代表每一种长度为 \(k+1\) 的 \(01\) 串。
若能得出图 \(G_k\) 的哈密顿回路,则在 \(G_{k}\) 中删掉这些边后,剩下的图中每个点恰为一条出边一条入边,形成若干个环。
注意到哈密顿回路必然和任意环点有交。我们扭转交点处的两条出边,即可将该环插入到哈密顿回路所在的环中。我们添加若干个环直到边数不小于 \(n - (k+1) + 1 = n-k\)。此时容易构造一条路径使得经过了哈密顿回路上的所有边,且总长度恰好为 \(n-k\)。不难验证此时同时满足了关于 \(k\) 和 \(k+1\) 的两条限制。
关于图 \(G_k\) 的哈密顿回路求法:
- 直接搜索。证明留做习题。
- 注意到图 \(G_k\) 的哈密顿回路是图 \(G_{k-1}\) 的欧拉回路。跑欧拉回路即可。
代码
# include <bits/stdc++.h>
const int N=1000010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n,k;
int b[N],bc;
bool vis[N];
int nex[N];
void dfs(int x){
if(vis[x]) return;
vis[x]=true,dfs((2*x)%(1<<k)),dfs((2*x+1)%(1<<k));
b[++bc]=x;
}
int main(void){
n=read();
for(;(1<<k)+(k-1)<=n;) ++k; --k;
dfs(0); std::reverse(b+1,b+1+bc);
if(n==(1<<k)+k-1){
for(int i=1;i<k;++i) putchar('0');
for(int i=1;i<=bc;++i) putchar('0'+(b[i]&1));
return 0;
}
memset(vis,false,sizeof(vis));
memset(nex,-1,sizeof(nex));
for(int i=1;i<=bc;++i) b[i]=(b[i]<<1|(b[i+1]&1)),vis[b[i]]=true;
for(int i=1;i<=bc;++i) nex[b[i]]=b[i%bc+1];
for(int i=0;i<(1<<(k+1));++i) if(nex[i]==-1) nex[i]=nex[i^(1<<k)]^1;
for(int i=0;i<(1<<(k+1));++i){
if(vis[i]) continue;
for(int j=i;!vis[j];j=nex[j]) vis[j]=true,++bc;
std::swap(nex[i],nex[i^(1<<k)]);
if(bc+k>=n){
for(int j=k;j>=0;--j) putchar('0'+((nex[i]>>j)&1));
for(int j=k+2,p=nex[nex[i]];j<=n;++j,p=nex[p]) putchar('0'+(p&1));
exit(0);
}
}
return 0;
}
AGC046E Permutation Cover
题解
何时无解?感性理解,一个元素出现太多或者太少都是不好的。考虑 \(k = 2\) 的情形,显然必须有 \(\max(a_1,a_2) \leq 2\min(a_1,a_2)\),最优的排布方法肯定是 \(\{2,1,2,2,1,2,2,1,2\}\) 这样。如果一个 \(2\) 到上一个 \(2\) 和下一个 \(2\) 的中间都没有 \(1\) 那肯定不合法。
拓展到 \(k\) 更大的情形,设 \(a_x,a_y\) 分别是最小值和最大值。不难发现 \(a_y \leq 2a_x\) 这一条件仍然是必要的。下面证明这一条件充分:
- 按照每次在序列末尾追加元素的方式构造答案。
- 如果 \(a_x = a_y\),则追加 \({1,2,\cdots,k}\),并将所有 \(k\) 减去 \(1\);
- 否则,将 \(\{1,2,3,\cdots,k\}\) 划分为两个集合 \(S,T\),其中若 \(a_i = a_x\) 则划分到集合 \(S\),否则划分到集合 \(T\)。按照 \(T,S,T\) 的顺序追加,并将 \(a_i (i \in S)\) 减去 \(1\),\(a_j (j \in T)\) 减去 \(2\)。
接下来仍然有难点:求字典序最小解。
枚举下一次覆盖结束点,即:枚举 \(l = 1,2,\cdots,k\),并检查是否可以往当前序列末端添加一个长度为 \(l\) 的序列,使得添加完之后,新序列的末尾 \(k\) 个恰好是一个排列,同时保证接下来会有解。那么求出字典序最小的合法序列作为这一步添加的序列即可。特殊地,第一次只枚举 \(l = k\)。
因为我们钦定了新序列的末尾 \(k\) 个是一个排列,所以当 \(l\) 固定的时候,要添加的元素集合是固定的。考察该集合是否能以任意顺序排列:
-
求出新的 \(a\) 数组,记作 \(b\)。类似地定义 \(b_x,b_y\)。
-
如果 \(b_y \leq 2b_x\),那么接下来一定有解。因此可以将该集合从小到大排列,以保证字典序最小;
-
如果 \(b_y > 2b_x + 1\),那么根据和上面类似的证明,无论以什么顺序排布,接下来都一定无解;
-
如果 \(b_y = 2b_x + 1\),接下来是有解的!这和上面的情况不同。注意到,如果只有 \(1,2,3,3,3\) 这五个元素,不管怎么排布都是无解的。但是如果前面的序列末尾是 \([1,2]\),我们就可以把这五个元素安排成 \([3,3,1,2,3]\)。第一个 \(3\) 虽然没办法和后面的元素组成排列,但是可以和前面的序列末尾组成排列 \([1,2,3]\)。
所以这种情况下只是需要精心安排位置。观察发现,我们在后面的构造中,让出现次数等于 \(b_y\) 的元素能够「蹭到」该集合里面出现次数等于 \(b_x\) 的元素,于是该集合在排列的时候不能把出现次数等于 \(b_y\) 的元素排在出现次数等于 \(b_x\) 的元素后面。除此之外没有限制。据此贪心放置即可。
代码
# include <bits/stdc++.h>
const int N=100010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int k,n;
typedef std::vector <int> poly;
poly a;
poly p,cur;
inline int getmx(const poly &a){
assert(a.size()>=k+1);
int mx=0;
for(int i=1;i<=k;++i) mx=std::max(mx,a[i]);
return mx;
}
inline int getmn(const poly &a){
assert(a.size()>=k+1);
int mn=INF;
for(int i=1;i<=k;++i) mn=std::min(mn,a[i]);
return mn;
}
inline void calc(int l){
poly b=a; poly vis(k+1,0);
for(int i=1;i<=k-l;++i) vis[p[p.size()-i]]=1;
for(int i=1;i<=k;++i) if(!vis[i]) --b[i];
int mxv=getmx(b),mnv=getmn(b);
if(mnv*2+1<mxv) return;
poly q;
if(mnv*2>=mxv){
for(int i=1;i<=k;++i) if(!vis[i]) q.push_back(i);
return cur=std::min(cur,q),void();
}
int pos=0;
for(int i=1;i<=k;++i) if(!vis[i]&&b[i]==mxv) pos=i;
for(int i=1;i<=k;++i){
if(vis[i]) continue;
if(i>pos||b[i]!=mnv) q.push_back(i);
if(i==pos){
for(int j=1;j<=i;++j) if(!vis[j]&&b[j]==mnv) q.push_back(j);
}
}
return cur=std::min(cur,q),void();
}
int main(void){
k=read(),a=poly(k+1,0);
for(int i=1;i<=k;++i) a[i]=read(),n+=a[i];
if(getmn(a)*2<getmx(a)) puts("-1"),exit(0);
while(p.size()<n){
cur=poly(1,INF);
for(int l=(!p.size())?k:1;l+p.size()<=n&&l<=k;++l) calc(l);
for(auto v:cur) p.push_back(v),--a[v];
}
for(auto v:p) printf("%d ",v);
return 0;
}
Gym103446L Three,Three,Three
题解
仍然要先考虑无解的条件。感受一下,发现 \(m = \frac32n\),输出是 \(m/3\) 行,这个数字恰好是 \(n/2\)。猜一下发现有解的充要条件是:图存在完美匹配。
考虑证明。
- 如果图存在完美匹配,则删去所有匹配边,图中每个点度数变为 \(2\),即图被分为若干个环。对环随意定向,并认为一条边被这条边的终点管辖。那么,找出每个匹配 \((u,v)\),则依次经过 \(u\) 的管辖边,\((u,v)\),\(v\) 的管辖边可以找到一条长度为 \(3\) 的路径。
- 如果存在解,那么取出每条路径中间两个点匹配,得到的必然是图的一组完美匹配。因为这一步中如果一个点被多次取出则度数至少为 \(4\)。
因此,选用一种一般图最大匹配算法即可构造出答案。此处为随机化算法。
代码
# include <bits/stdc++.h>
const int N=1505,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
std::mt19937 rng(114514);
int n,m;
bool vis[N];
std::vector <std::array <int,2> > G[N];
int mat[N];
int _u[N],_v[N];
bool del[N];
bool match(int x){
if(G[x].size()>1) for(int _=1;_<=5;++_)
std::swap(G[x][rng()%G[x].size()],G[x][rng()%G[x].size()]);
vis[x]=true;
for(int i=0;i<(int)G[x].size();++i){
int y=G[x][i][0];
if(vis[y]) continue; vis[y]=true;
if(!mat[y]||match(mat[y])){
mat[x]=y,mat[y]=x;
return true;
}
}
return false;
}
int p[N];
int ans[N],siz;
int to[N];
inline void solve(void){
for(int i=1;i<=n;++i) p[i]=i; std::shuffle(p+1,p+1+n,rng);
for(int i=1;i<=n;++i) std::shuffle(G[i].begin(),G[i].end(),rng);
memset(mat,0,sizeof(mat));
int cur=0;
for(int i=1;i<=n;++i){
if(!mat[p[i]]){
for(int _=1;_<=5;++_){
memset(vis,false,sizeof(vis));
if(match(p[i])) {++cur; break;}
}
}
}
if(siz<cur) siz=cur,memcpy(ans,mat,sizeof(ans));
return;
}
int main(void){
n=read(),m=read();
for(int i=1;i<=m;++i){
int u=read(),v=read(); G[u].push_back({v,i}),G[v].push_back({u,i}); _u[i]=u,_v[i]=v;
}
for(int T=1;T<=10;++T) solve();
if(siz!=n/2) printf("IMPOSSIBLE"),exit(0);
for(int i=1;i<=n;++i){
if(i<mat[i]){
for(int j=1;j<=m;++j){
if(!del[j]&&(i==_u[j]&&mat[i]==_v[j]||i==_v[j]&&mat[i]==_u[j])){
del[j]=true; break;
}
}
}
}
memset(vis,false,sizeof(vis));
for(int i=1;i<=n;++i){
if(vis[i]) continue;
for(int x=i;;){
int y=0; for(auto e:G[x]) if(!del[e[1]]) {y=e[0]; del[e[1]]=true; break;}
assert(y); to[y]=x; vis[x]=true; if(y==i) break;
x=y;
}
}
for(int i=1;i<=n;++i) if(mat[i]<i) printf("%d %d %d %d\n",to[i],i,mat[i],to[mat[i]]);
return 0;
}
AT_hitachi2020_e Odd Sum Rectangles
题解
转化为 \(2^n\) 行 \(2^m\) 列的二维前缀异或和数组 \(s\)。矩形 \((u,d] \times (l,r]\) 的值的奇偶性等于 \(s_{d,r} \oplus s_{d,l} \oplus s_{u,r} \oplus s_{u,l}\),即选取两行两列的四个位置来异或。
根据均值不等式,那么我们希望两行异或得到的 \(2^m\) 列中,为 \(0/1\) 的列数量尽可能接近。
取 \(s_{i,j} = \operatorname{popcount}(i \& j) \& 1\) 即可使得两行异或得到的为 \(0/1\) 的列数量完全相同。
代码
# include <bits/stdc++.h>
const int N=2005,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n,m;
int a[N][N];
int main(void){
n=(1<<read())-1,m=(1<<read())-1;
for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) a[i][j]=(__builtin_popcount(i&j)&1);
for(int i=n;i;--i) for(int j=m;j;--j) a[i][j]^=(a[i][j-1]^a[i-1][j]^a[i-1][j-1]);
for(int i=1;i<=n;++i,puts("")){
for(int j=1;j<=m;++j) printf("%d",a[i][j]);
}
return 0;
}
Part 2: 打表 (小范围搜索)
打表过题也算过吗?
Codeforces 1906L Palindromic Parentheses
题解
打表发现,字典序最小解有好的规律。这里不加描述地直接给出代码,大家也可以尝试自己打个表。
代码
# include <bits/stdc++.h>
const int N=100010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n,k;
int ans[N];
int main(void){
n=read(),k=read();
if(k<n/2||k==n) puts("-1"),exit(0);
if(n%4==0){
for(int i=k+1;i<=n;++i) ans[i]=1;
for(int i=1;i<=(k-n/2)/2;++i) ans[2*i]=ans[k+1-2*i]=1;
if(k%2) ans[(k+1)/2]=1;
}else{
for(int i=k+1;i<=n;++i) ans[i]=1;
for(int i=1;i<=(k-n/2)/2;++i) ans[2*i]=ans[k+1-2*i]=1;
if(k%2==0) ans[(k+1-n/2)]=1;
}
for(int i=1;i<=n;++i) putchar("()"[ans[i]]);
return 0;
}
CCPC Online A 军训 I
题解
操作太多次肯定和操作 \(O(1)\) 次等价。进一步发现本质不同的操作只有:
- 什么都不做;
- 做一次操作:U,D,L,R;
- 做两次操作:UL,UR,DL,DR,LU,LD,RU,RD。
更长的操作序列都可以简化。对于出现了多个 U/D,L/R 的情况,和只保留最后一次出现是等价的。据此得到 \(k > 13\) 全部无解。利用单次 \(O(k2^{nm}\operatorname{poly}(nm))\) 的暴力运行若干组 \(n,m\) 较小的数据后寻找规律即可。
代码 (by H_W_Y)
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+5;
int n,m,mp[N][N],k;
bool fl;
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
void NO(){cout<<"No\n";}
void YES(){
cout<<"Yes\n";
if(!fl){
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) cout<<(mp[i][j]?'*':'-');
cout<<'\n';
}
}else{
for(int j=1;j<=m;j++){
for(int i=1;i<=n;i++) cout<<(mp[i][j]?'*':'-');
cout<<'\n';
}
}
}
void DO1(){
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) mp[i][j]=1;
YES();
}
void DO2(){
for(int i=1;i<=n;i++) mp[i][1]=1;
YES();
}
void DO3(){
if(m<=2) return NO();
for(int i=1;i<=n;i++) mp[i][2]=1;
YES();
}
void DO5(){
if(gcd(n,m)==1) return NO();
int d=gcd(n,m);
for(int c=1;c<=d;c++){
for(int i=(c-1)*(n/d)+1;i<=c*(n/d);i++)
for(int j=(c-1)*(m/d)+1;j<=c*(m/d);j++)
mp[i][j]=1;
}
YES();
}
void DO4(){
mp[1][1]=1;
YES();
}
void DO6(){
mp[1][2]=1;
YES();
}
void DO7(){
if(n==2) mp[1][2]=mp[2][1]=1;
else{
for(int i=2;i<=m;i++) mp[1][i]=1;
mp[2][1]=1;
}
YES();
}
void DO9(){
if(n==2){
mp[2][1]=mp[1][3]=1;
}else mp[2][2]=1;
YES();
}
void DO11(){
if(n==2){
if(m<=3) return NO();
mp[2][1]=mp[1][2]=mp[1][4]=1;
}else mp[1][m]=mp[2][1]=1;
YES();
}
void DO13(){
mp[1][1]=mp[n][m]=1;
YES();
}
void SOLVE(){
cin>>n>>m>>k;fl=0;
if(n>m) swap(n,m),fl=1;
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) mp[i][j]=0;
if(k>13||k==8||k==10||k==12) return NO();
if(k==1) return DO1();
if(n<=1&&m<=1) return NO();
if(k==2) return DO2();
if(k==5) return DO5();
if(k==3) return DO3();
if(n==1) return NO();
if(k==4) return DO4();
if(m<=2) return NO();
if(k==6) return DO6();
if(k==7) return DO7();
if(k==9) return DO9();
if(k==11) return DO11();
if(n<=2) return NO();
if(k==13) return DO13();
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int _;cin>>_;
while(_--) SOLVE();
return 0;
}
朴实无华的生成器
# include <bits/stdc++.h>
const int N=100010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n,m;
int c[10][10];
inline int id(int x,int y){
return (x-1)*m+y-1;
}
inline int v(int s,int x){
return (s>>x)&1;
}
int d[10][10];
inline void solveL(int arr[][10]){
for(int i=1;i<=n;++i){
int cnt=0;
for(int j=1;j<=m;++j) cnt+=arr[i][j];
for(int j=1;j<=m;++j) arr[i][j]=(j<=cnt);
}
return;
}
inline void solveR(int arr[][10]){
for(int i=1;i<=n;++i){
int cnt=0;
for(int j=1;j<=m;++j) cnt+=arr[i][j];
for(int j=1;j<=m;++j) arr[i][m-j+1]=(j<=cnt);
}
return;
}
inline void solveU(int arr[][10]){
for(int j=1;j<=m;++j){
int cnt=0;
for(int i=1;i<=n;++i) cnt+=arr[i][j];
for(int i=1;i<=n;++i) arr[i][j]=(i<=cnt);
}
return;
}
inline void solveD(int arr[][10]){
for(int j=1;j<=m;++j){
int cnt=0;
for(int i=1;i<=n;++i) cnt+=arr[i][j];
for(int i=1;i<=n;++i) arr[n-i+1][j]=(i<=cnt);
}
return;
}
inline void rcopy(void){
memcpy(d,c,sizeof(d));
return;
}
inline int val(int arr[][10]){
int s=0;
for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) s=((s<<1)|arr[i][j]);
return s;
}
inline void cover(int arr[][10],int s){
for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) arr[i][j]=v(s,id(i,j));
return;
}
int ret[20];
int pr[10][10];
int main(void){
n=read(),m=read();
int mask=(1<<(n*m))-1;
memset(ret,-1,sizeof(ret));
for(int s=1;s<=mask;++s){
std::set <int> S;
cover(c,s);
rcopy(),S.insert(val(d));
rcopy(),solveL(d),S.insert(val(d));
rcopy(),solveR(d),S.insert(val(d));
rcopy(),solveU(d),S.insert(val(d));
rcopy(),solveD(d),S.insert(val(d));
rcopy(),solveL(d),solveU(d),S.insert(val(d));
rcopy(),solveL(d),solveD(d),S.insert(val(d));
rcopy(),solveR(d),solveU(d),S.insert(val(d));
rcopy(),solveR(d),solveD(d),S.insert(val(d));
rcopy(),solveU(d),solveL(d),S.insert(val(d));
rcopy(),solveU(d),solveR(d),S.insert(val(d));
rcopy(),solveD(d),solveL(d),S.insert(val(d));
rcopy(),solveD(d),solveR(d),S.insert(val(d));
if(ret[S.size()]==-1) ret[S.size()]=s;
}
for(int i=0;i<=13;++i){
if(ret[i]==-1) continue;
printf("i = %d ret = %d\n",i,ret[i]);
if(ret[i]!=-1){
cover(pr,ret[i]);
for(int x=1;x<=n;++x){
for(int y=1;y<=m;++y) printf("%d",pr[x][y]);
puts("");
}
}
}
return 0;
}
[CTS2024] 众生之门
题解
打表发现答案不超过 \(3\)。
进一步地,答案奇偶性固定,所以只需要检验答案是 \(0/1\) 还是 \(2/3\)。
同时,我们还发现,取到最小值的解是不少的,解的大小可以近似看作在 \([0,n]\) 内均匀分布。于是我们随机化 \(O(n)\) 次就很可能就能找到一组解。猜测除了 \(n\) 比较小的时候,以及树是菊花的情况,答案全部都 \(\leq 1\)。特判掉这些情况(如果 \(n\) 比较小,直接跑暴力;否则,怎么排列都是一样的)
当然,我们不能盲目蛮干。随机排列的复杂度肯定不能是 \(O(n)\) 的,我们可以先随机一个排列,然后随机交换相邻两项。为了减少常数,记得使用 \(O(1)\) LCA。
代码
/*
I know this sky loves you
いずれ全て
変わってしまったって
空は青いだろうよ
*/
# include <bits/stdc++.h>
const int N=50010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int p[N];
int n,s,t;
std::vector <int> G[N];
int dfn[N],dep[N],tc,mx[N][21],fa[N];
void dfs(int x,int fa){
dfn[x]=++tc,dep[x]=dep[fa]+1,mx[tc][0]=x,::fa[x]=fa;
for(auto y:G[x]){
if(y==fa) continue;
dfs(y,x);
}
return;
}
inline int cmp(int x,int y){
return dep[x]<dep[y]?x:y;
}
inline void init(void){
for(int k=1;k<=17;++k)
for(int i=1;i+(1<<k)-1<=n;++i) mx[i][k]=cmp(mx[i][k-1],mx[i+(1<<(k-1))][k-1]);
return;
}
inline int lca(int u,int v){
if(u==v) return u;
u=dfn[u],v=dfn[v]; if(u>v) std::swap(u,v); ++u;
int k=std::__lg(v-u+1);
return fa[cmp(mx[u][k],mx[v-(1<<k)+1][k])];
}
inline int dis(int u,int v){
return dep[u]+dep[v]-2*dep[lca(u,v)];
}
inline void print(void){
for(int i=1;i<=n;++i) printf("%d ",p[i]); puts("");
return;
}
std::mt19937 rng(114514);
inline bool flower(void){
int dec=0; for(int i=1;i<=n;++i) if(G[i].size()>1) ++dec;
return dec<=1;
}
int g[N];
inline void calc(void){
if(flower()) return print();
if(n<=10){
int ans=INF;
memcpy(g,p,(n+5)*4);
do{
int cur=0;
for(int i=2;i<=n;++i) cur^=dis(p[i-1],p[i]);
if(ans>cur) ans=cur;
if(ans<=1) break;
}while(std::next_permutation(p+2,p+n));
memcpy(p,g,(n+5)*4);
do{
int cur=0;
for(int i=2;i<=n;++i) cur^=dis(p[i-1],p[i]);
if(ans==cur) return print();
}while(std::next_permutation(p+2,p+n));
}else{
int T=std::min(30*n,400000);
int ans=0;
for(int i=2;i<=n;++i) ans^=dis(p[i-1],p[i]);
while(T--){
int x=rng()%(n-2)+2,y=rng()%(n-2)+2;
if(x==y) continue;
ans^=dis(p[x-1],p[x])^dis(p[x],p[x+1])^dis(p[y-1],p[y])^dis(p[y],p[y+1]);
std::swap(p[x],p[y]);
ans^=dis(p[x-1],p[x])^dis(p[x],p[x+1])^dis(p[y-1],p[y])^dis(p[y],p[y+1]);
if(ans<=1) return print();
}
return print();
}
return;
}
inline void solve(void){
n=read(),s=read(),t=read(),tc=0;
p[1]=s,p[n]=t;
for(int i=2,j=1;i<n;++i){ while(j==s||j==t) ++j; p[i]=j++;}
for(int i=1;i<=n;++i) G[i].clear();
for(int i=1;i<n;++i){
int u=read(),v=read(); G[u].push_back(v),G[v].push_back(u);
}
dfs(1,0),init();
calc();
return;
}
int main(void){
int T=read();
while(T--) solve();
return 0;
}
Part 3. 强化限制
这部分构造的自由度通常有点太高,我们可以假装解还满足别的限制。
AGC035C Skolem XOR Tree
题解
猜测树高只有 \(O(1)\) 层,因为树的形态越复杂我们构造的时候越不好控制。
首先还是发现,\(n = 2^k\) 的时候是没有解的。另外,异或是有性质的:任意四个连续数的异或和都是 \(0\)。这启发我们对这些数分成若干组,组间之间不干扰。
注意到把 \(1\) 当根的时候,对于每个 \(i \bmod 2 = 0\),我们把 \((i,i+1)\) 分成一组,然后构造一组 \(i+1 \to i \to 1 \to i+n+1 \to i+n\) 的链,最后把 \(n+1\) 挂到 \(3\) 的下面组成链 \(n+1 \to 3 \to 2 \to 1\) 即可。
最后的问题是 \(n \bmod 2 = 0\) 的情况。我们判掉了 \(n = 2^k\) 的情况,遂猜测 \(n\) 的连边可能跟 \(n\) 的 popcount 至少是 \(2\) 有点关系。事实也是如此,令 \(v\) 为 \(n\) 的 lowbit,则 \(v\) 也是偶数。构造链 \(n \to n+v+1 \to 1 \to n-v\to 2n\) 即可。上述链不会破坏之前构造出的结构,因为 \(1\) 此时和编号小于 \(n\) 的偶数点、编号大于 \(n+1\) 小于 \(2n\) 的奇数点都有连边。
代码
# include <bits/stdc++.h>
const int N=100010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n;
int main(void){
if(__builtin_popcount(n=read())==1) puts("No"),exit(0);
puts("Yes");
for(int i=2;i+1<=n;i+=2){
printf("%d %d\n%d %d\n%d %d\n%d %d\n",1,i,1,i+n+1,i,i+1,i+n,i+n+1);
}
printf("%d %d\n",3,n+1);
if(n%2==0){
int v=n&-n; printf("%d %d\n%d %d\n",n,n+v+1,2*n,n-v);
}
return 0;
}
Codeforces 804E The same permutation
题解
结合上 Part 1 的技巧,首先考虑:什么时候无解?注意到交换要改变逆序对奇偶性,那么 \(n(n-1)/2\) 如果不是偶数就无解了。因此 \(n \bmod 4 \leq 1\)。
这个时候已经只剩下 \(n \bmod 4 = 0,n \bmod 4 = 1\) 的两种情况了。先来考虑 \(n \bmod 4 = 0\) 的情况。
一种合理的尝试是将元素按 \(4\) 个一组分组。因为具体是什么元素不重要,于是我们可以假装分组是 \((1,2,3,4),(5,6,7,8),\cdots,\) 这样。
搜索发现存在一系列操作刚好消耗完组内的 \(6\) 个操作;同时,存在一系列操作能够消耗完两组间的所有 \(16\) 个操作(这个其实也是可以搜出来的,大致思路是:我们感知一下,可以把 \(16\) 个操作分成 \(4\) 组,使得每组内每个元素只参与恰好 \(1\) 次交换;这样搜索复杂度就大大减少了)。因此按照任意顺序执行组内 / 组外操作即可。
有了 \(n \bmod 4 = 0\) 的情况,对于 \(n \bmod 4 = 1\) 的情况,就不太困难了。我们只需要在适当的时候插入有 \(n\) 参与的操作就行了。具体地,对于一个组内操作 \((x,y)\),其中 \(x \bmod 2 = 1,y = x+1\),我们可以等价替换为 \((x,n),(x,y),(y,n)\)。
代码
# include <bits/stdc++.h>
const int N=100010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n,v[N];
std::vector <std::array <int,2> > ans;
inline void oper(std::array <int,2> s,bool flag=false){
if(flag&&(n&1)&&(s[0]%2)&&(s[0]+1==s[1])){
ans.push_back({s[0],n}),ans.push_back({s[0],s[1]}),ans.push_back({s[1],n});
}else ans.push_back(s);
std::swap(v[s[0]],v[s[1]]);
return;
}
inline void inblo(int l){
--l;
oper({l+1,l+2},true);
oper({l+1,l+3},true);
oper({l+2,l+4},true);
oper({l+1,l+4},true);
oper({l+2,l+3},true);
oper({l+3,l+4},true);
return;
}
inline void betblo(int l,int r){
--l,--r; // (a b c d) (b c d a) (d a b c) (c d a b)
oper({l+1,r+1});
oper({l+2,r+2});
oper({l+3,r+3});
oper({l+4,r+4});
oper({l+1,r+2});
oper({l+2,r+3});
oper({l+3,r+4});
oper({l+4,r+1});
oper({l+1,r+4});
oper({l+2,r+1});
oper({l+3,r+2});
oper({l+4,r+3});
oper({l+1,r+3});
oper({l+2,r+4});
oper({l+3,r+1});
oper({l+4,r+2});
return;
}
int main(void){
n=read(),std::iota(v+1,v+1+n,1);
if(n==1) return puts("YES"),0;
if(n%4>1) return puts("NO"),0;
for(int i=1;i<=n/4;++i) inblo((i-1)*4+1);
for(int i=1;i<=n/4;++i){
for(int j=i+1;j<=n/4;++j) betblo((i-1)*4+1,(j-1)*4+1);
}
for(int i=1;i<=n;++i) assert(v[i]==i);
puts("YES");
for(auto w:ans) printf("%d %d\n",w[0],w[1]);
return 0;
}
Part 4. 归纳构造
\(n \to n+k\);\(n \to n-k\);\(n \to kn\)。
UOJ496 新年的新航线
题解
(From KING_OF_TURTLE)
对于 \(n > 4\) 的情形:
考虑多边形最外侧的三角形 \((u,v,w)\),设 \(w\) 是外侧点,可以发现与 \(w\) 相邻的两条边中必定删除恰好一条。
先删除这两条边,然后给三角形的内侧边 \((u,v)\) 打上一个标记 \(w\),表示之后 \(w\) 要向 \((u,v)\) 两个点中的恰好一个连边。
接下来,我们每次考虑删除的时候,要考虑边上的标记。对于最外侧的三角形 \((u,v,w)\),设 \(w\) 为外侧的点,分情况讨论:
- \((u,w)\) 和 \((v,w)\) 均无标记:将 \(w\) 打到 \((u,v)\) 上;
- \((u,w)\) 和 \((v,w)\) 中恰有一个有标记:设 \((u,w)\) 有标记,把标记点和 \(w\) 都连到 \(u\) 上面;(因为 \(u\) 成为外侧点的时候还要连至少一条边所以是 OK 的)
- \((u,w)\) 和 \((v,w)\) 均有标记:将标记点都连到 \(w\) 上,再把 \(w\) 打到 \((u,v)\) 上。
\(n = 4\) 简单讨论或直接搜索均可。
代码
# include <bits/stdc++.h>
const int N=500010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n,du[N];
std::vector <int> G[N];
bool del[N];
std::map <std::pair <int,int>,int> tag;
inline int find(int u,int v){
if(u>v) std::swap(u,v);
return tag[std::make_pair(u,v)];
}
inline void join(int u,int v,int w){
if(u>v) std::swap(u,v);
tag[std::make_pair(u,v)]=w;
return;
}
std::vector <std::pair <int,int> > ans;
inline void res(int u,int v){
ans.push_back(std::make_pair(u,v));
return;
}
int main(void){
n=read();
if(n==3) puts("-1"),exit(0);
for(int i=1;i<=n-3;++i){
int u=read(),v=read();
G[u].push_back(v),G[v].push_back(u),++du[u],++du[v];
}
for(int i=1;i<=n;++i){
int u=i,v=i%n+1;
G[u].push_back(v),G[v].push_back(u),++du[u],++du[v];
}
std::queue <int> q;
for(int i=1;i<=n;++i) if(du[i]==2) q.push(i);
for(int T=1;T<=n-4;++T){
int i=q.front(),u=0,v=0;
q.pop(),del[i]=true;
for(auto j:G[i]){
--du[j];
if(!del[j]){
if(!u) u=j;
else v=j;
if(du[j]==2) q.push(j);
}
}
int tu=find(i,u),tv=find(i,v);
if(!tu&&!tv){
join(u,v,i);
}else if(tu&&tv){
res(tu,i),res(tv,i);
join(u,v,i);
}else if(tu){
res(tu,u),res(i,u);
}else res(tv,v),res(i,v);
}
std::vector <int> d2,d3;
for(int i=1;i<=n;++i) if(!del[i]){
if(du[i]==2) d2.push_back(i);
else d3.push_back(i);
}
bool l[2]={false,false};
if(find(d2[0],d3[0])) res(find(d2[0],d3[0]),d3[0]),l[0]=true;
if(find(d2[1],d3[0])) res(find(d2[1],d3[0]),d3[0]),l[0]=true;
if(find(d2[0],d3[1])) res(find(d2[0],d3[1]),d3[1]),l[1]=true;
if(find(d2[1],d3[1])) res(find(d2[1],d3[1]),d3[1]),l[1]=true;
if(!l[0]&&!l[1]) res(d3[0],d3[1]),res(d3[0],d2[0]),res(d3[0],d2[1]);
else if(l[0]&&l[1]) res(d3[0],d3[1]),res(d2[0],d3[0]),res(d2[1],d3[1]);
else{
if(l[1]) std::swap(d3[0],d3[1]);
res(d3[0],d3[1]),res(d3[0],d2[0]),res(d3[0],d2[1]);
}
for(auto v:ans) printf("%d %d\n",v.first,v.second);
return 0;
}
QOJ7756 Omniscia Spares None
题解
「换斗移星,谋事在人」
对于 \(n \leq 4\) 的情况是平凡的。对于 \(n = 5,6\) 的情况目测无解。对于 \(n = 7,9\) 的情况均无解,但 \(n = 8,n = 10\) 的情况均有解。
手玩应该是可以玩出来的,但是草稿纸弄掉了,火大。这里贴一个别人的构造吧:
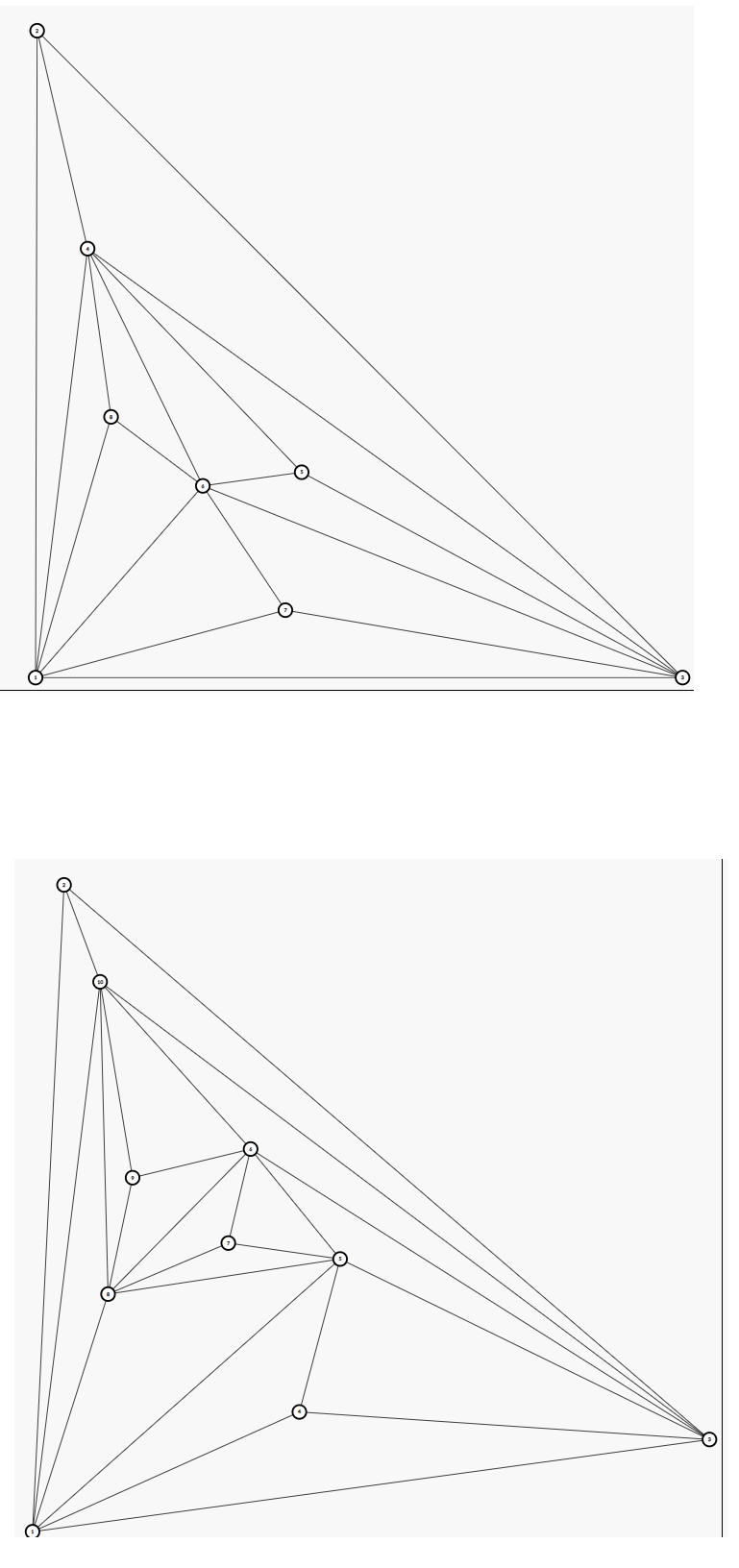
在构造的过程中,我们尽可能把度数小于 \(6\) 的点往外放,力求增量构造的时候把之前度数小于 \(6\) 的点变为度数不小于 \(6\) 的点。尝试之后,发现可以放出来两个度数为 \(3\) 的点。因此,一种增量构造方法如下:
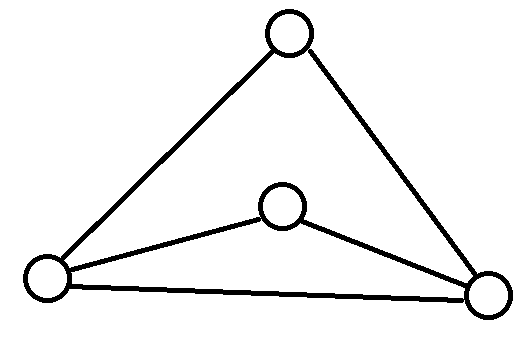
此时最上方和内部的点度数为 \(3\),左右两角的点度数为 \(6\)。
使用这种方法添加了 \(4\) 个点并保持了原来的结构。
因为我们有 \(n = 8,10\) 的构造,可以按照这种方法构造出其余偶数的解。大胆猜测 \(n\) 是偶数都有解,\(n\) 是奇数则无解。
代码略。
Codeforces 715D Create a Maze
题解
注意到 \(n,m,k\) 的级别仅为 \(O(\log T)\),这启发我们要若干个乘 \(k\) 加 \(b\) 的操作。
用 \(2 \times 2\) 实现乘 \(2\) 加 \(0/1\) 是简单的,如下图:
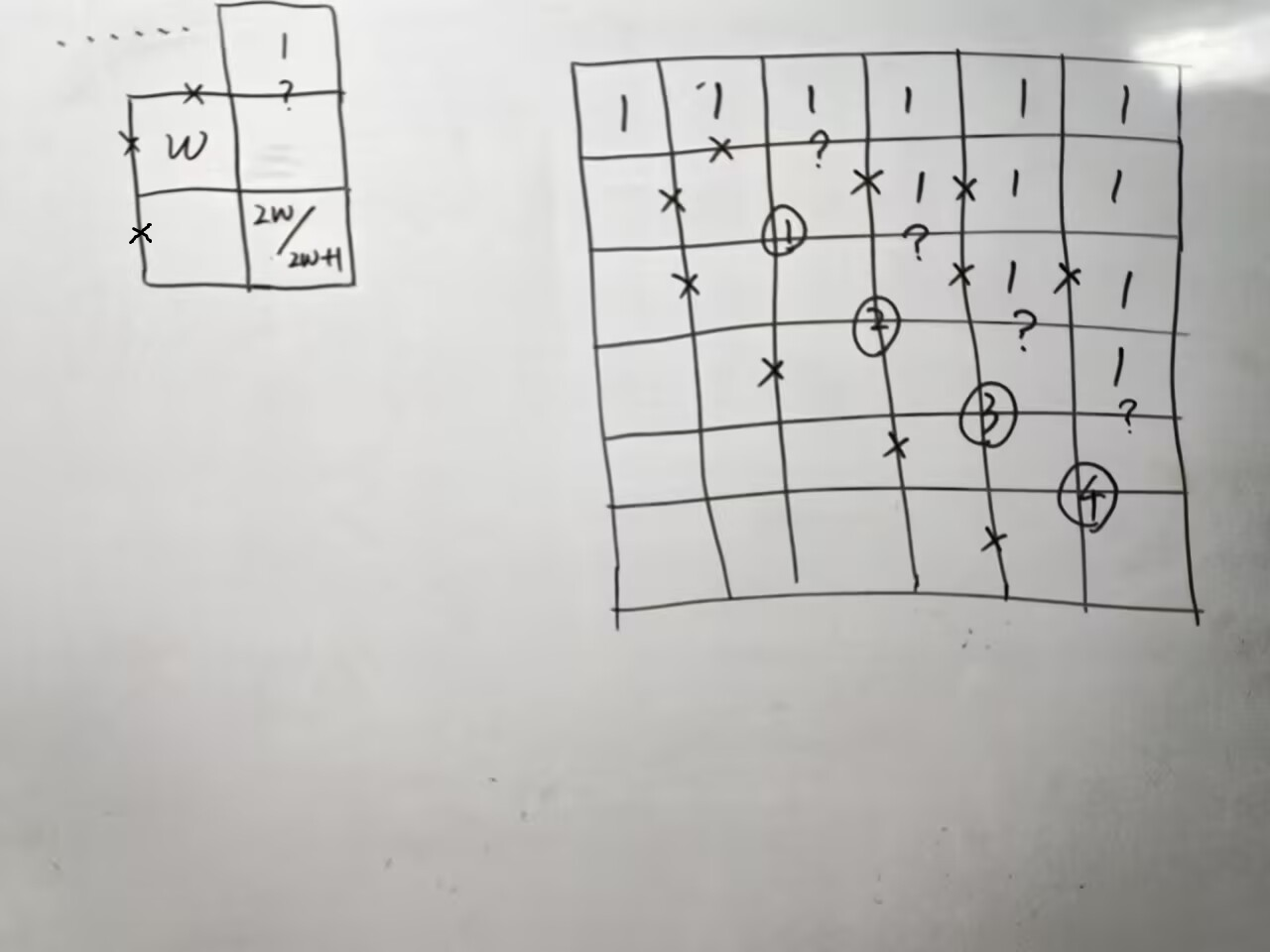
但是这道题限制相当紧,无法通过。我们发现我们对左侧的利用不够:左侧和上侧都可以利用,但是因为进制取得太小,导致左侧只能被完全封上。
尝试取 \(3 \times 3\) 进行基本构造。
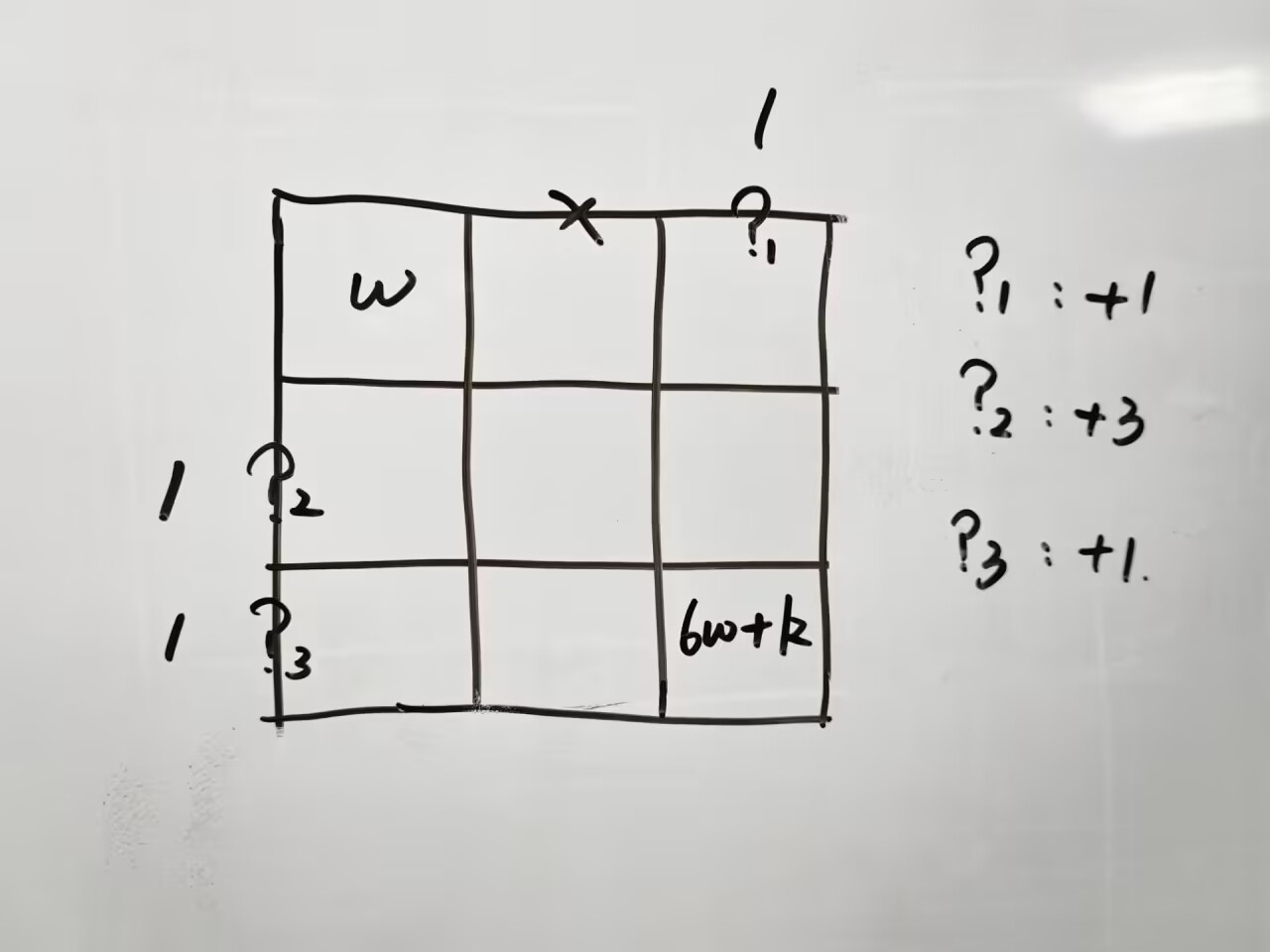
这样,组合三个 \(?\) 处的开 / 关,可以实现 \(3 \times 3\) 完成乘 \(6\) 加 \(k(0 \leq k < 6)\),足以通过本题。
取其它进制或者进行合理的随机化也可以通过,可以自行查阅其它题解。
代码
# include <bits/stdc++.h>
const int N=100010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
typedef long long ll;
ll T;
std::vector <int> d;
int n;
std::vector <std::array <int,4> > vec;
inline void init(int x){
n+=2;
vec.push_back({n-4,n,n-3,n});
vec.push_back({n-6,n-1,n-5,n-1});
vec.push_back({n,n-4,n,n-3});
vec.push_back({n-1,n-6,n-1,n-5});
vec.push_back({n,n-1,n+1,n-1});
vec.push_back({n-2,n,n-2,n+1});
vec.push_back({n-1,n,n-1,n+1});
vec.push_back({n,n-2,n+1,n-2});
vec.push_back({n-3,n-1,n-2,n-1});
if(x<3) vec.push_back({n-1,n-3,n-1,n-2}); else x-=3;
if(x<2) vec.push_back({n,n-3,n,n-2}); else --x;
if(x<1) vec.push_back({n-3,n,n-2,n});
return;
}
inline bool chk(std::array <int,4> v){
if(v[0]<1||v[1]<1||v[2]>n||v[3]>n) return false;
return true;
}
int main(void){
scanf("%lld",&T);
while(T) d.push_back(T%6),T/=6;
std::reverse(d.begin(),d.end());
n=2; vec.push_back({2,1,2,2}),vec.push_back({1,2,2,2});
for(auto x:d) init(x);
int sum=0;
for(auto v:vec) sum+=chk(v);
printf("%d %d\n",n,n);
printf("%d\n",sum);
for(auto v:vec) if(chk(v)){
for(auto w:v) printf("%d ",w); puts("");
}
return 0;
}
Part 5. 图论构造杂项
都看到这里了,来看点开心的东西吧。
图上二选一构造
通常是用 DFS 树这个结构。被 EA 锐评:出这个简直有病!
来源:【学习笔记】一类图上二选一构造问题 - duyiblue - 博客园。原文总结得相当到位,这里就不补充了。
图上转圈构造
题 1
把⼀个 \(n\) 个点的完全图的所有边排成一个环,使得任意连续的 \(n-1\) 条边都构成一棵树。
解
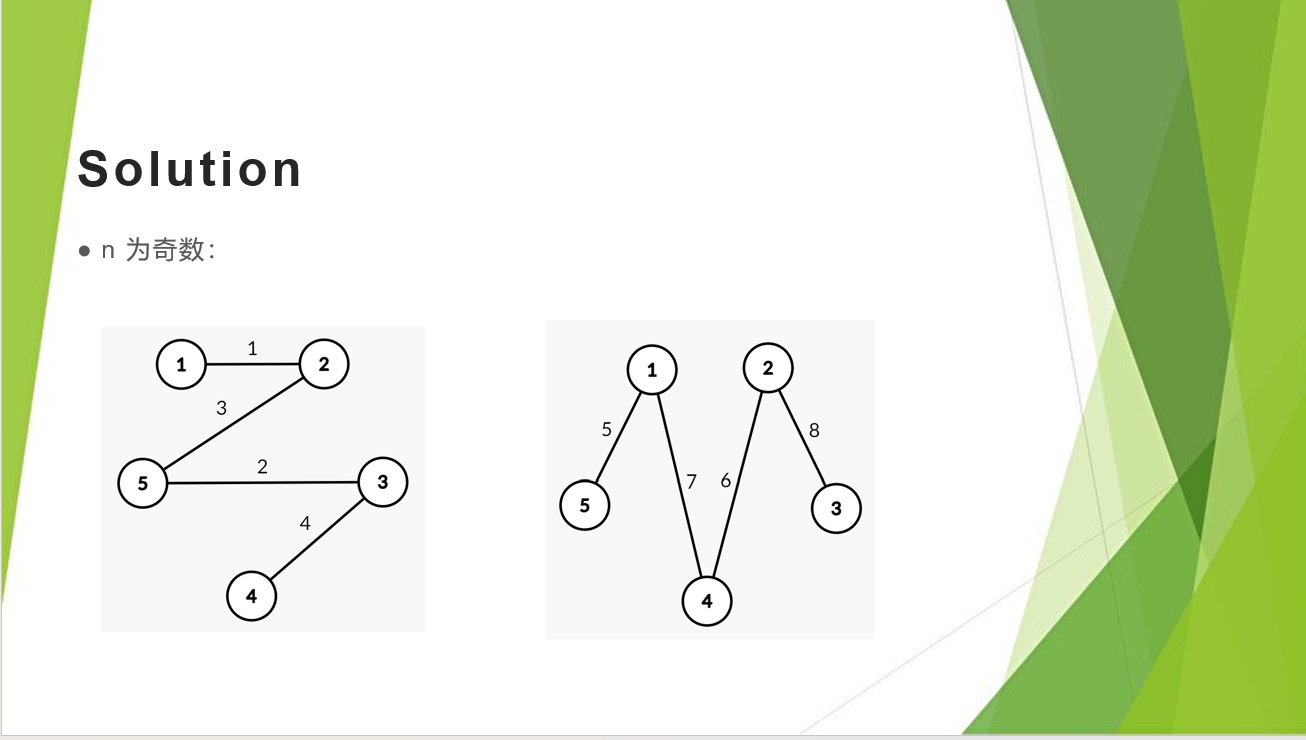
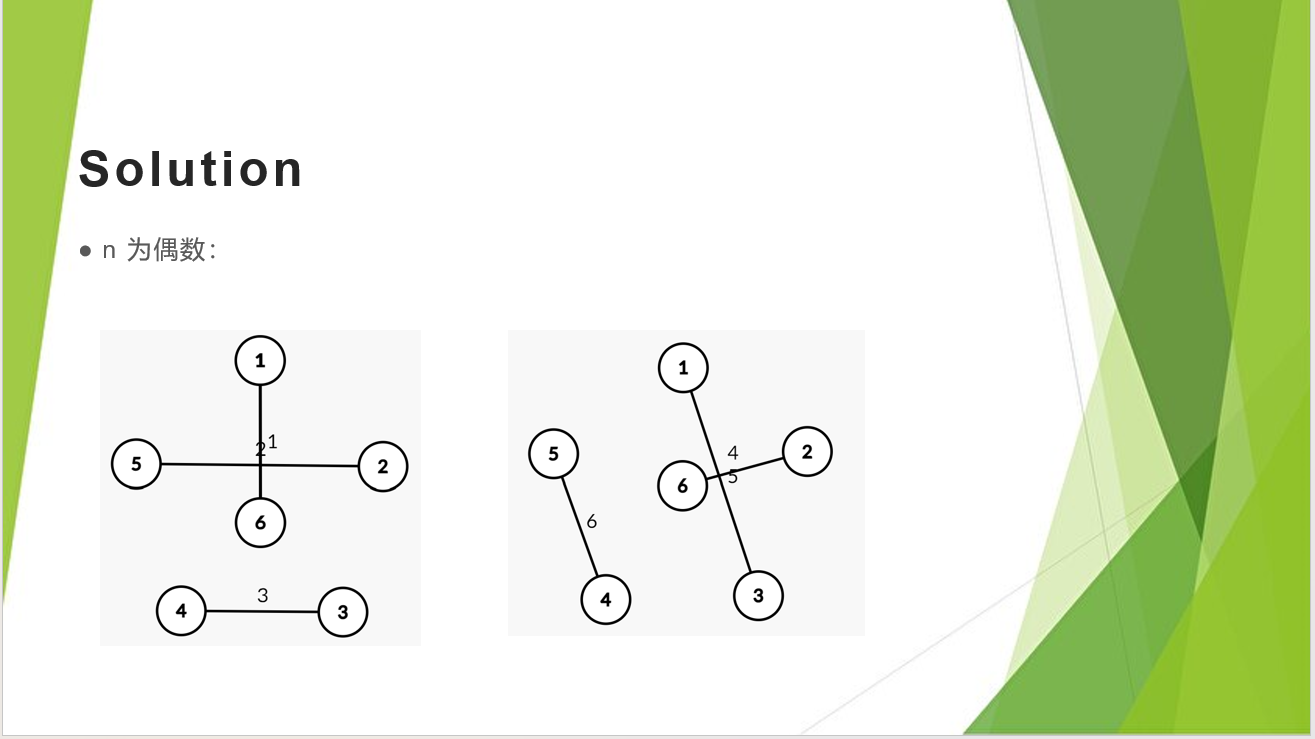
题 2.1
把一个 \(n\) 个点的完全图分成 \(n-1\) 组匹配,\(n\) 为偶数。
解
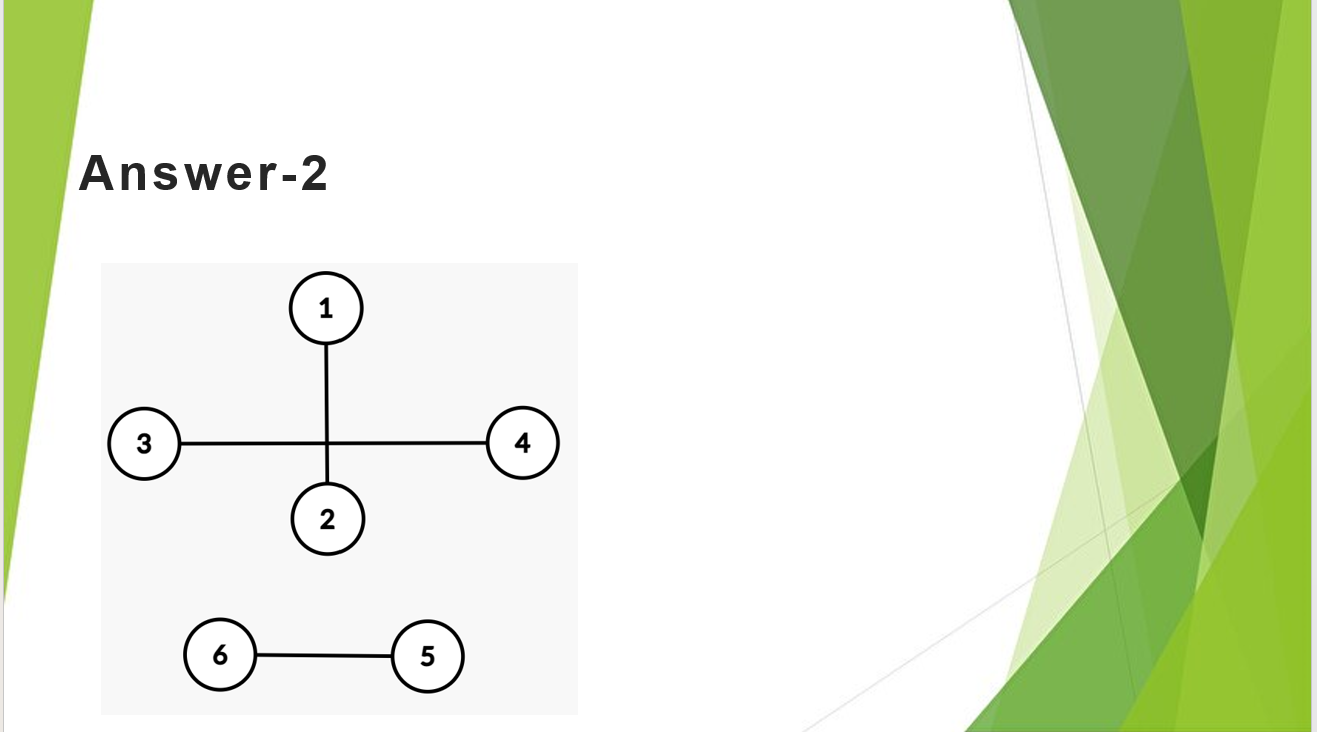
题 2.2
把一个 \(n\) 个点的完全图分成 \(n/2\) 组哈密顿路,\(n\) 为偶数。
解
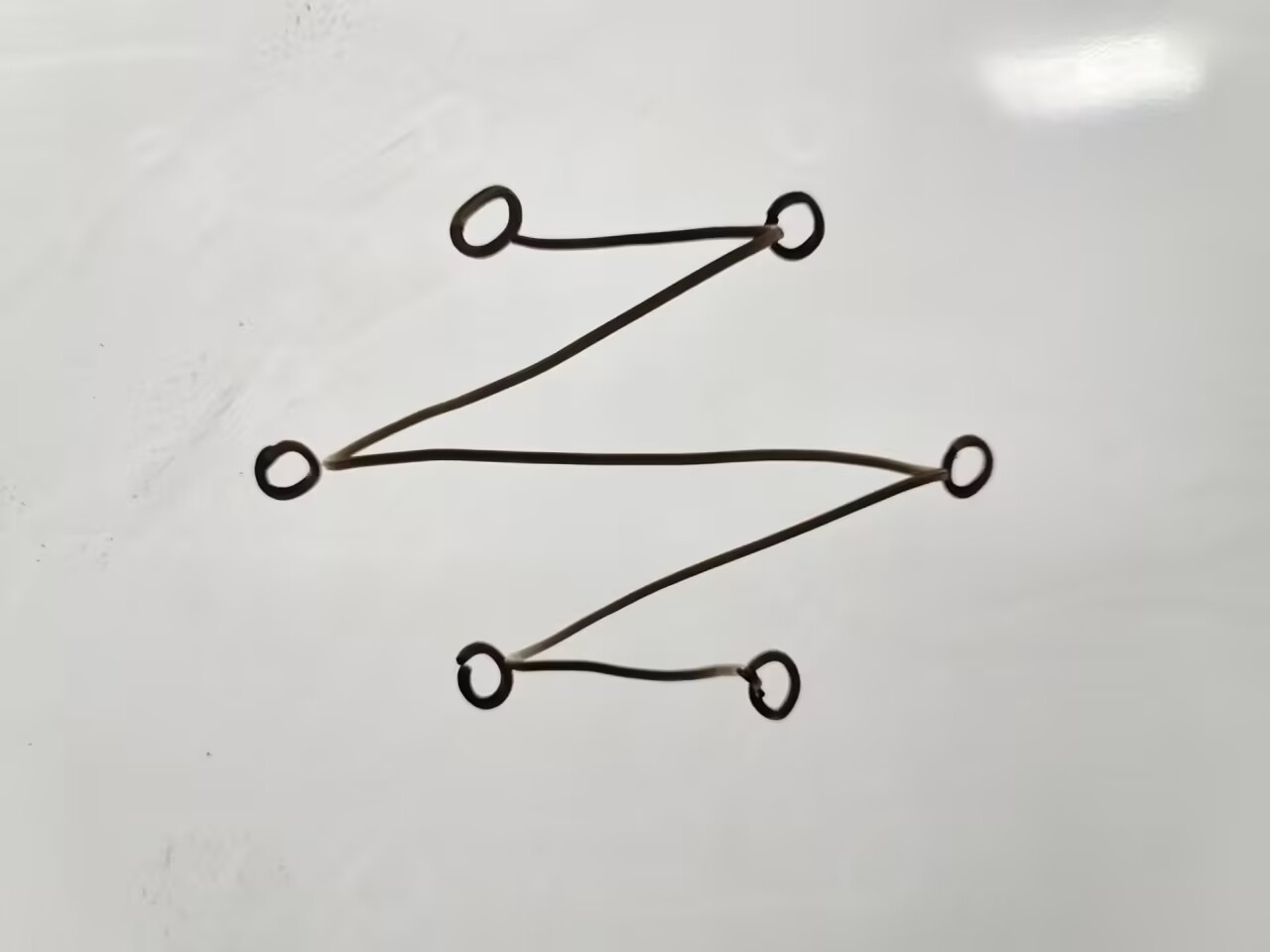
题 2.3
把一个 \(n\) 个点的完全图分成 \(\dfrac {n-1}{2}\) 组哈密顿回路,\(n\) 为奇数。
解
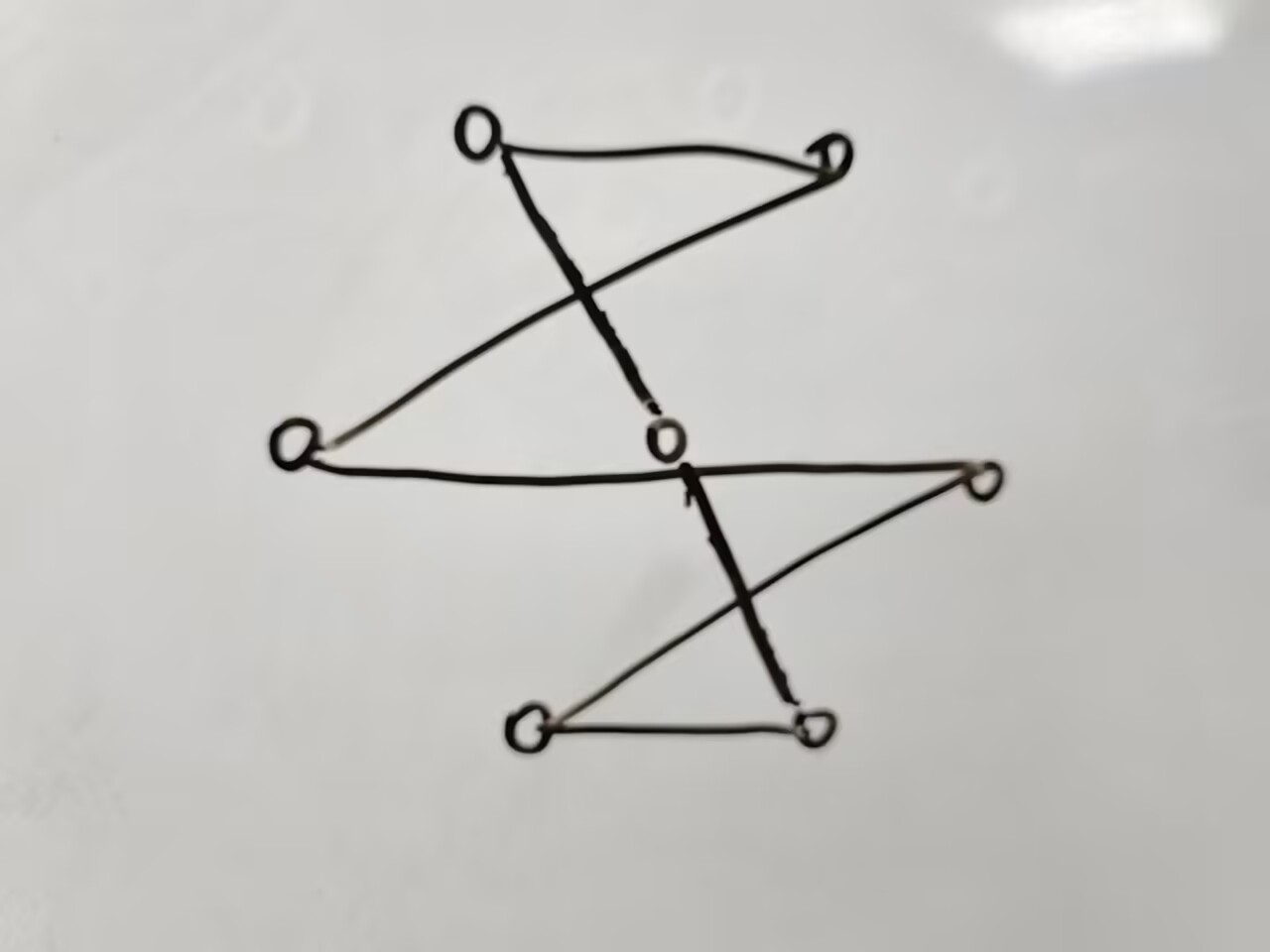
Part 6. 实战
Codeforces 341E Candies Game
题解
考虑有三堆大小分别为 \(x,y,z\) 的糖果时怎么做。
设 \(y = kx + b\)。对 \(k\) 二进制拆分,从低到高考虑 \(k\) 的每一位,设当前位位权为 \(2^{l}\):
- 若 \(k\) 的 \(2^l\) 位为 \(1\),则执行操作 \((x,y)\),此时 \(k\) 的 \(2^{l}\) 位被夺去,\(x\) 翻倍;
- 若 \(k\) 的 \(2^l\) 位为 \(0\),则执行操作 \((x,z)\)(不难验证仍有 \(x \leq z\)),此时 \(x\) 翻倍。
那么操作后 \(y\) 变为 \(b\)。排序后,新的 \(x',y',z'\) 满足 \(x' < \frac{1}{2}x\)。
\(O(\log^2 V)\) 次减少一堆,于是总次数大概是 \(O(n \log^2 V)\) 的,可以通过。
代码
# include <bits/stdc++.h>
const int N=100010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n;
int a[N];
std::vector <int> idx;
inline int val(void){
idx.clear();
for(int i=1;i<=n;++i) if(a[i]) idx.push_back(i);
return (int)idx.size();
}
std::vector <std::array <int,2> > ans;
inline void move(int x,int y){
assert(a[x]<=a[y]); ans.push_back({x,y}); a[y]-=a[x],a[x]*=2;
return;
}
inline void solve(int x,int y,int z){
if(a[x]>a[y]) std::swap(x,y); if(a[y]>a[z]) std::swap(y,z); if(a[x]>a[y]) std::swap(x,y);
int k=a[y]/a[x];
for(int i=0;i<=std::__lg(k);++i){
if((k>>i)&1) move(x,y); else move(x,z);
}
return;
}
int main(void){
n=read();
for(int i=1;i<=n;++i) a[i]=read();
if(val()<=1) puts("-1"),exit(0);
while(val()>=3) solve(idx[0],idx[1],idx[2]);
printf("%d\n",(int)ans.size());
for(auto v:ans) printf("%d %d\n",v[0],v[1]);
return 0;
}
Codeforces 538G Berserk Robot
题解
先判断奇偶性是否合法。
考虑进行坐标转换:\((x,y) \to (\frac{x+y+t}{2},\frac{y-x+t}{2})\)。本质上是,先旋转坐标系使得两维度独立,再加上 \(t\) 使得坐标变化量非负。
这样,两维是独立的。接下来以 \(x\) 这一维举例。我们本质上想求一个周期内的位移 \(v\)。为此,对于第 \(i\) 条信息 \((t_i,x_i)\),我们记录 \(k_i = \lfloor t_i / l \rfloor\),\(w_i = t_i \bmod l\)。将信息按照 \(w\) 排序之后(因为有边界情况,我们加入信息 \((k = 0,w = 0)\) 和 \((k = -1, w= l)\) ),考虑相邻两项。
注意到一个周期的位移是 \(v\),周期内 \(w_{i-1}\) 到 \(w_i\) 这段时间的位移可以是 \([0,\Delta w]\),那么我们有限制:
- \(\Delta x - w \leq \Delta k \times v \leq \Delta x\)
解不等式即可。
如果有解我们可以根据 \(v\) 和 \(k_i,x_i\) 还原出第 \(w_i\) 秒应该在哪个位置。那么有构造:如果当前还没走到那个位置,就增加坐标,否则在那个位置旁边横跳即可。如果奇偶性是正确的,这个办法总是可行。
代码
# include <bits/stdc++.h>
const int N=200010,INF=0x3f3f3f3f;
typedef long long ll;
inline ll read(void){
ll res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n,l;
struct Node{
ll t,x,y,k,w;
bool operator < (const Node &rhs) const{
return (w!=rhs.w)?(w<rhs.w):(k<rhs.k);
}
}p[N];
template <typename T> inline void cmax(T &a,T b){
a=std::max(a,b);
}
template <typename T> inline void cmin(T &a,T b){
a=std::min(a,b);
}
int main(void){
n=read(),l=read();
for(int i=1;i<=n;++i){
ll t=read(),x=read(),y=read(); // (x+y+t)/2, (y-x+t)/2
if((t&1)!=((x+y)&1)) puts("NO"),exit(0);
p[i].t=t,p[i].x=(x+y+t)/2,p[i].y=(y-x+t)/2;
p[i].k=t/l,p[i].w=t%l;
}
p[++n].k=-1,p[n].w=l;
p[++n].k=0,p[n].w=0;
std::sort(p+1,p+1+n);
ll xmin=0,xmax=l,ymin=0,ymax=l;
for(int i=2;i<=n;++i){
ll k=p[i].k-p[i-1].k;
ll w=p[i].w-p[i-1].w;
ll dx=p[i].x-p[i-1].x,dy=p[i].y-p[i-1].y;
if(k==0){
if(!(dx-w<=0&&0<=dx)) puts("NO"),exit(0);
if(!(dy-w<=0&&0<=dy)) puts("NO"),exit(0);
}else if(k>0){
ll l=(ll)ceill(1.0L*(dx-w)/k),r=(ll)floorl(1.0L*dx/k);
cmax(xmin,l),cmin(xmax,r);
l=ceill(1.0L*(dy-w)/k),r=(ll)floorl(1.0L*dy/k);
cmax(ymin,l),cmin(ymax,r);
}else{
k*=-1;
ll l=(ll)ceill(1.0L*(-dx)/k),r=(ll)floorl(1.0L*(-dx+w)/k);
cmax(xmin,l),cmin(xmax,r);
l=(ll)ceill(1.0L*(-dy)/k),r=(ll)floorl(1.0L*(-dy+w)/k);
cmax(ymin,l),cmin(ymax,r);
}
}
if(xmin>xmax||ymin>ymax) puts("NO"),exit(0);
std::vector <int> xm,ym;
for(int i=2;i<=n;++i){
if(p[i].w==p[i-1].w) continue;
ll pre=p[i-1].x-p[i-1].k*xmin,cur=p[i].x-p[i].k*xmin;
int td=p[i].w-p[i-1].w;
for(int j=1;j<=td;++j) if(pre<cur) xm.push_back(1),++pre; else xm.push_back(0);
pre=p[i-1].y-p[i-1].k*ymin,cur=p[i].y-p[i].k*ymin;
for(int j=1;j<=td;++j) if(pre<cur) ym.push_back(1),++pre; else ym.push_back(0);
}
for(int i=0;i<l;++i) putchar("DLRU"[xm[i]<<1|ym[i]]);
return 0;
}
Codeforces 1276E Four Stones
题解
仍然是要先考虑判断无解的。将石子排序之后差分,不难观察到差分的 \(\gcd\) 是不变的,于是,如果两个状态的差分 \(\gcd\) 不同就无解。同时奇偶性也是不会变的,于是还要检查奇偶性。
否则石子的坐标总能够直接表示为 \(x = x'g+ r\)。接下来讨论所有石子的坐标均已经变化为 \(x'\) 的情形,此时差分 \(\gcd\) 是 \(1\)。
注意到操作可逆。我们想办法从起始状态和终止状态出发,得到两个比较简单的状态,如果能够在这两个比较简单的状态之间移动,那么就解决了。
这里一个简单的状态是:位置的极差 \(\leq 1\)。更进一步地,我们会移动到 \([p,p+1]\) 处,其中 \(p\) 是一个偶数。考虑如何达到这个状态。
设石子的位置为 \(x_1 \leq x_2 \leq x_3 \leq x_4\),\(\Delta = x_4 - x_1\)。如果 \([x_1+1/4\Delta,x_4 - 1/4\Delta]\) 中间有某个 \(x_2\) 或者 \(x_3\),那么将 \(x_1,x_4\) 中离这个 \(x_2 / x_3\) 更近的那一个翻到另一侧去,可以让 \(\Delta\) 变为原来的至多 \(3/4\)。
否则,我们记 \(d_2 = \min(x_2 - x_1,x_4 - x_2),d_3 = \min(x_3-x_1,x_4 - x_3)\)。此时都有 \(d_2 ,d_3 < 1/4 \Delta\)。考虑快速增大 \(d_2,d_3\) 使得其中某一个达到至少 \(1/4 \Delta\),就可以执行上面的操作了。
考虑如下操作:将 \(a\) 沿着 \(b,c\) 翻折,\(a\) 会先变为 \(2b-a\),再变为 \(2c - (2b - a) = a+ 2(c-b)\)。那么 \(d_2,d_3\) 中较小的那个总能够通过这种方式来增加较大的那个的两倍。不难发现 \(O(\log \Delta)\) 次后就会变得符合条件。
设起始状态和终止状态分别移动到了 \([p_s,p_s+1]\) 和 \([p_t,p_t+1]\)。我们希望将 \([p_s,p_s+1]\) 移动到 \([p_t,p_t+1]\) 处。不妨设 \(p_s < p_t\),有一个简单的每次平移 \(2\) 的方法:执行两次「将 \(x_1,x_2,x_3\) 对着 \(x_4\) 翻折」的操作。此时操作次数太多,无法通过。
注意到每次移动的距离等于二倍极差。同时,执行「将 \(x_3\) 对着 \(x_1\) 翻折,\(x_2\) 对着 \(x_4\) 翻折」的操作会使得极差变为原来的至少两倍。于是,我们可以采取这样的方法:先按照这种方法增大极差,直到极差即将超过 \(p_t - p_s\),然后执行平移。平移后,如果当前极差已经超过 \(p_t - p_s\),则撤销一次这种操作,减少极差。
这样总操作次数是 \(O(\log^2 V)\) 级别的,大部分时候不太满,可以通过此题。
代码
# include <bits/stdc++.h>
const int N=100010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
typedef long long ll;
typedef std::array <ll,2> po;
std::vector <po> A,B;
std::vector <po> ra,rb;
inline void sym(std::vector <po> &s,std::vector <po> &ret,int i,int j,bool real=false){
if(real){
for(int x=0;x<=3;++x) if(s[x][1]==i){i=x; break;}
for(int x=0;x<=3;++x) if(s[x][1]==j){j=x; break;}
}
s[i][0]=2*s[j][0]-s[i][0];
ret.push_back({s[i][1],s[j][1]});
}
inline void chk(std::vector <po> &s){std::sort(s.begin(),s.end());}
inline void gather(std::vector <po> &s,std::vector <po> &ret){
for(;;){
chk(s);
ll d=s[3][0]-s[0][0]; assert(d);
if(d==1) break;
bool flag=false;
for(int j=1;j<=2;++j){
if(s[j][0]>=s[0][0]+d/4.0&&s[j][0]<=s[3][0]-d/4.0){
if(s[j][0]-s[0][0]<=s[3][0]-s[j][0]) sym(s,ret,0,j);
else sym(s,ret,3,j);
flag=true; break;
}
}
if(flag) continue;
ll dl=std::min(s[1][0]-s[0][0],s[3][0]-s[1][0]);
ll dr=std::min(s[2][0]-s[0][0],s[3][0]-s[2][0]);
if(dl<dr){// [0 1] [2 3]
if(s[1][0]-s[0][0]==dl){
if(s[3][0]-s[2][0]==dr) sym(s,ret,1,2),sym(s,ret,1,3); // [2,3]
else sym(s,ret,1,0),sym(s,ret,1,2); // [0,2]
}else{
if(s[3][0]-s[2][0]==dr) sym(s,ret,1,3),sym(s,ret,1,2);
else sym(s,ret,1,2),sym(s,ret,1,0);
}
}else{
if(s[3][0]-s[2][0]==dr){
if(s[1][0]-s[0][0]==dl) sym(s,ret,2,1),sym(s,ret,2,0); // [0,1]
else sym(s,ret,2,3),sym(s,ret,2,1); // [1,3]
}else{
if(s[1][0]-s[0][0]==dl) sym(s,ret,2,0),sym(s,ret,2,1);
else sym(s,ret,2,1),sym(s,ret,2,3);
}
}
}
chk(s);
if(s[0][0]&1) for(int j=0;j<=3;++j) if(s[j][0]!=s[3][0]) sym(s,ret,j,3);
chk(s);
return;
}
inline ll myabs(ll x){return x>0?x:-x;}
inline void slide(void){
ll s=A[0][0],t=B[0][0];
if(s==t) return;
std::vector <po> ex;
ll l=myabs(t-s)/2; bool fl=false;
for(;;){
chk(A); ll d=A[3][0]-A[0][0];
if(l==0&&d==1) break;
while(!fl&&d<l){
chk(A); sym(A,ex,2,0),sym(A,ex,1,3); chk(A);
ll _d=A[3][0]-A[0][0];
d=_d;
ra.push_back(ex[ex.size()-2]),ra.push_back(ex[ex.size()-1]);
}
if(fl) fl=false;
if(d>l){
fl=true;
auto u=ex[ex.size()-2],v=ex[ex.size()-1];
sym(A,ra,v[0],v[1],true),sym(A,ra,u[0],u[1],true);
ex.pop_back(),ex.pop_back();
continue;
}
l-=d;
for(int _=0;_<=1;++_){
chk(A);
if(s<t) for(int i=0;i<=2;++i) sym(A,ra,i,3);
else for(int i=1;i<=3;++i) sym(A,ra,i,0);
}
}
return;
}
int main(void){
A.resize(4),B.resize(4);
for(int i=0;i<=3;++i) A[i][0]=read(),A[i][1]=i;
for(int i=0;i<=3;++i) B[i][0]=read(),B[i][1]=i;
auto C=A;
std::sort(A.begin(),A.end()); std::sort(B.begin(),B.end());
ll ga=0,gb=0,d=0;
for(int i=1;i<=3;++i) ga=std::__gcd(A[i][0]-A[0][0],ga),gb=std::__gcd(B[i][0]-B[0][0],gb);
if(ga!=gb||(ga!=0&&(A[0][0]%ga!=B[0][0]%gb))) puts("-1"),exit(0);
if(ga==0){
if(A[0][0]==B[0][0]) puts("0"),exit(0);
else puts("-1"),exit(0);
}
d=A[0][0]%ga;
for(int i=0,c[2]={0,0};i<=3;++i){
A[i][0]=(A[i][0]-d)/ga,B[i][0]=(B[i][0]-d)/gb;
++c[A[i][0]&1],--c[B[i][0]&1];
if(i==3&&(c[0]||c[1])) puts("-1"),exit(0);
}
gather(A,ra),gather(B,rb);
slide();
chk(A);
for(int i=0;i<=3;++i) assert(A[i][0]==B[i][0]);
std::vector <int> bid(4);
for(int i=0;i<=3;++i) bid[B[i][1]]=A[i][1];
while(rb.size()) ra.push_back({bid[rb.back()[0]],bid[rb.back()[1]]}),rb.pop_back();
std::vector <po> real_ans;
for(auto v:ra){
if(C[v[0]][0]!=C[v[1]][0]) real_ans.push_back({C[v[0]][0],C[v[1]][0]});
C[v[0]][0]=2*C[v[1]][0]-C[v[0]][0];
}
printf("%d\n",(int)real_ans.size());
for(auto v:real_ans) printf("%lld %lld\n",v[0],v[1]);
return 0;
}
Codeforces 1053E Euler tour
题解
考虑对于一个给定的序列 \(a_1,a_2,\cdots,a_{2n-1}\),判定是否合法:
- \(a_1 = a_{2n - 1}\);
- 对于任意 \(a_l = a_r\),\(r-l\) 应该是偶数;
- 对于任意 \(a_l = a_r\),\((l,r)\) 应该恰好出现 \((r-l)/2\) 种数;
- 对于每种数,第一次出现位置和最后一次出现位置构成的区间,要么包含要么不交。
现在可以开始做了。设我们在处理 \([l,r]\) 这个区间,我们想要 \([l,r]\) 刚好是一棵完整的子树。那么 \(a_l = a_r\) 必须成立(或者有 \(a_l = a_r = 0\)),且 \(r-l\) 应该是偶数。接下来处理区间内部,我们遍历 \((l,r)\) 每一个非零位置 \(a_x\),并且找到下一个和 \(a_x\) 相等的位置 \(a_y\)。如果 \(y\) 在区间外部那么已经非法,否则 \((x,y)\) 也构成一棵完整的子树,我们就把 \([x,y]\) 缩成一个点 \(a_x\),然后找下一个可能存在的 \(y\)。重复该过程,此时 \((l,r)\) 内不会有相同数。
如果此时 \((l,r)\) 中出现的种类数大于 \((r-l)/2\),已经无解;否则在区间开头的若干个 \(0\) 处填上新出现的数。接下来采用如下方式填上剩余的 \(0\):
- 首先,若连续三个位置形如 \([0,a,b]\),则变为 \([b,a,b]\) 然后缩成单点 \(b\);对于 \([a,b,0]\) 同理。
- 因为此时 \((l,r)\) 中已经填上了 \((r-l)/2\) 个数,经过上面的步骤之后,必然不会有相邻的两个 \(0\),此时给区间填上子树的根一定是合法的。
使用链表维护做到线性。
代码
# include <bits/stdc++.h>
const int N=1000010,INF=0x3f3f3f3f;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-') f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int n,m;
int a[N];
int cur;
bool vis[N];
inline void wrong(void){
printf("no"),exit(0);
}
inline int newval(void){
while(cur<=n&&vis[cur]) ++cur;
if(cur>n) wrong();
return cur;
}
int pre[N],nex[N];
int mat[N],pos[N];
inline void del(int l,int r){
l=pre[l],r=nex[r];
pre[r]=l,nex[l]=r;
return;
}
inline void assign(int l,int r,int &x){
while(x>l&&nex[nex[x]]<=r&&!a[x]&&a[nex[x]]&&a[nex[nex[x]]]){
a[x]=a[nex[nex[x]]],del(nex[x],nex[nex[x]]),x=pre[pre[x]];
}
while(x>l&&nex[nex[x]]<=r&&a[x]&&a[nex[x]]&&!a[nex[nex[x]]]){
a[nex[nex[x]]]=a[x],
del(nex[x],nex[nex[x]]),x=pre[pre[x]];
}
return;
}
void solve(int l,int r){
if((r-l+1)%2==0) wrong();
for(int i=l;i<=r;i=nex[i]){
while(mat[i]){
if(mat[i]>r) wrong();
solve(nex[i],pre[mat[i]]),del(nex[i],mat[i]),mat[i]=mat[mat[i]];
}
}
int cur=0,tot=0,rt=a[pre[l]];
for(int i=l;i<=r;i=nex[i]) cur+=(a[i]!=0),++tot;
tot=tot/2+1;
if(cur>tot) wrong();
for(int i=l;i<=r;i=nex[i]) if(cur<tot&&!a[i]) a[i]=newval(),vis[a[i]]=true,++cur;
for(int i=l;i<=r;i=nex[i]) assign(pre[l],r,i);
for(int i=l;i<=r;i=nex[i]) if(!a[i]) a[i]=rt;
return;
}
int main(void){
n=read(),m=2*n-1;
for(int i=1;i<=m;++i) a[i]=read(),vis[a[i]]=true;
if(n==1) printf("yes\n%d",1),exit(0);
for(int i=2;i<=m;++i) if(a[i]&&a[i-1]&&a[i]==a[i-1]) wrong();
if(a[1]&&a[m]&&a[1]!=a[m]) wrong();
a[1]=a[m]=(a[1]?a[1]:a[m]);
for(int i=1;i<=m;++i) pre[i]=i-1,nex[i]=i+1;
pre[0]=0,nex[0]=1,nex[m+1]=m+1,pre[m+1]=m;
for(int i=m;i;--i){
if(!a[i]) continue;
mat[i]=pos[a[i]],pos[a[i]]=i;
}
solve(1,m);
printf("yes\n");
for(int i=1;i<=m;++i) printf("%d ",a[i]);
return 0;
}
如果确实是构造爱好者的话!
请看 [AGC043E] Topology,zhouershan 认证好题。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号