2023 信友队暑期集训
由于我懒,本 Blog 只记录暑期集训的难题 & 趣题 & 我写得很爽的题,当然大部分难题我都不会做。
事实上,因为这篇博客是 7.19 开始写的,所以后面会比前面详细很多(
当然这篇 Blog 更倾向日记风格。
补题列表:D1T2
杭师大的饭虽然不难吃,但是感觉不如 wz,不甚满意/ng
收手机,有点伤心。/ng
\(\textbf{7.11}\)
今晚九点,不见不散,郑荣叫爹!
扑克真的很好玩!尤其是看到 zr 睁大眼睛说你为什么还有三张 A 的时候(
真的是小丑/cf
\(\textbf{7.14}\)
\(\textbf{T3}\)
模拟赛放 Ynoi,兄弟。
\(\textbf{Description}\)
实现一个数据结构,要求实现三个操作:
- 在图中将两个点连边;
- 回退到某个历史版本;
- 查询所有点 \(x\) 可到达的点中所有点中点权第 \(k\) 大。
\(1\le n,m \le 10^5\) 。
\(\textbf{Sol.}\)
很显然的需要使用并查集。口胡了一个启发式合并:每个并查集维护一个 std::vector 当做平衡树维护点权集合。保存所有历史版本即可。但是数据太毒瘤了,全 RE。但是后来发现不写撤销操作能拿分,于是 \(14\text{pts}\) 滚粗。
暴力的瓶颈在于空间。本题最大的空间开销就是撤销操作需要回到历史版本。注意到不强制在线,考虑把所有的询问离线下来。
用 std::vector 之类的东西保存所有需要回退的版本编号,只有当当前版本在后续操作中用得到时才保存它。这样可以节省许多不必要的空间开销。
当然这个东西随便卡。而且代码也很难写。
容易将上述思路的「后续操作用得到时保存」转化为「不保存,直接以当前版本为基础完成所有后续操作」。
这和 dfs 是非常类似的:遍历,回溯。于是有一个新的思想:操作树。这个名词我也没听过,是老师讲的。不过也挺形象:由所有操作组成的树。
对于所有操作二,把当前操作编号和所给历史版本连边,对于操作一 & 三,把当前操作和上一个操作连边。
读入完询问之后对于操作树遍历一边即可。写一个类似可撤销并查集的东西即可,三个操作直接暴力干。
剩下的就是对分块基础的考验了()注意到本题的原题是 Ynoi,因此考虑分块。区间第 \(k\) 大,很显然的值域分块。
点权离散化之后最多 \(10^5\) 个值,对这 \(10^5\) 个值开桶然后对桶分块。
具体地,令 \(\text{cnt}(rt, k)\) 表示根为 \(rt\) 的并查集中,点权属于第 \(k\) 个块所表示的区间的个数。那么点权 \(k\,\text{th}\) 可以轻易地解决:整块扫描过去,直到 \(\sum_{i=1}^{p-1}\text{cnt}(rt,i)\le k\) 且 \(\sum_{i=1}^p\text{cnt}(rt,i)> k\) 。然后扫描原数组(离散化后)上第 \(p\) 个块对应的区间,从小到大枚举属于该并查集的值,什么时候刚好 \(k\) 个了直接 break 就行。
细节稍微注意一下,只要不是和我一样把乘写成除就行(
$\textbf{AC Code}$
#include <bits/stdc++.h>
// FastIO
typedef long long i64;
constexpr int N = 1e5 + 5;
constexpr int B = 3300;
int n, m, siz[N], fa[N], tot, ans[N];
unsigned short cnt[N][N / B + 5];
inline int find(int x) {
return x == fa[x] ? x : find(fa[x]);
}
struct Node { int val, id; } a[N];
struct que { int opt, x, y; } q[N];
struct Edge { int to, nxt; } E[N];
int head[N], idx;
inline void addEdge(int x, int y) {
E[++idx] = Edge{y, head[x]}, head[x] = idx;
}
inline void mrg(int x, int y) {
if(siz[x] > siz[y]) x ^= y ^= x ^= y;
fa[x] = y, siz[y] += siz[x];
for(int i = 1; i <= tot; i++) {
cnt[y][i] += cnt[x][i];
}
}
inline void del(int x, int y) {
if(siz[x] > siz[y]) x ^= y ^= x ^= y;
fa[x] = x, siz[y] -= siz[x];
for(int i = 1; i <= tot; i++) {
cnt[y][i] -= cnt[x][i];
}
}
inline int qry(int x, int k) {
int pos, res = 0;
x = find(x);
if(siz[x] < k) return -1;
for(int i = 1; i <= tot; i++) {
if(k > cnt[x][i]) k -= cnt[x][i];
else { pos = i; break; }
}
for(int i = (pos - 1) * B + 1; i <= pos * B; i++) {
if(find(a[i].id) == x && !(--k)) {
res = a[i].val;
break;
}
}
return res;
}
inline void dfs(int u) {
bool tag = 0;
int opt = q[u].opt, x = q[u].x, y = q[u].y;
if(opt == 1) {
x = find(x), y = find(y);
if(x ^ y) {
mrg(x, y);
tag = 1;
}
} else if(opt == 3) ans[u] = qry(x, y);
for(int i = head[u]; i; i = E[i].nxt) dfs(E[i].to);
if(tag) del(x, y);
}
signed main() {
read(n, m);
tot = (n - 1) / B + 1;
for(int i = 1; i <= n; i++) {
read(a[i].val);
a[i].id = fa[i] = i;
siz[i] = 1;
}
std::sort(a + 1, a + n + 1, [](Node& lhs, Node& rhs) {
return lhs.val < rhs.val;
});
for(int i = 1; i <= n; i++) {
cnt[a[i].id][(i - 1) / B + 1]++;
}
for(int i = 1; i <= m; i++) {
read(q[i].opt);
if(q[i].opt == 2) {
read(q[i].x);
addEdge(q[i].x, i);
} else {
read(q[i].x, q[i].y);
addEdge(i - 1, i);
}
}
dfs(0);
for(int i = 1; i <= m; i++) {
if(q[i].opt == 3) {
writeln(ans[i]);
}
}
return flush(), 0;
}
实际块长为 \(1000\) 左右的时候我的代码跑的最快。但是原题卡空间,所以块长设的比较大。
原题链接:[Ynoi2014] 等这场战争结束之后
\(\textbf{7.15}\)
\(\textbf{Exam #1}\)
考试时将是 5:30 - 9:00,时间挺长的。赛前还在想能不能 AK(
先开 T1。题目要求 \(\min\sum|\frac{x_i-x}{v_i}|\),绝对值之和显然要转化成和中位数相关的问题。思考了 10min 怎么把这玩意和中位数联系上来。然后发现读错题了,要求的是 \(\min\max\sum|\dots|\)。这不一眼?直接二分答案,check 也很好写,对每个 \(i\) 都能写出一个一次不等式,联立一下看一下解集是否非空即可。0.5h 切 T1,有点慢了(
开 T2,感觉像个 dp,好像有点难先放着。然后看 T3,这是什么?感觉很典但是一时没法看出什么思路。T4:什么神秘图论?我 Tarjan 都没学过我玩个毛线啊?
想了想还是先开 T2。不会 dp,开始想暴力。最开始思考对每个颜色处理需要达到其最大值的最小操作次数。赛时比较紧张感觉这个没错。然后代码不太会写,停了好久。大概 7:00 左右头脑突然清醒:这不随便 Hack?换了个思路,考虑莫队。类似莫队的区间转移,动态地去维护所有满足条件的区间,\(ans\) 即为过程中所有颜色的出现次数取 \(\max\) 即可。然后思考对什么分块。然后发现又降智了:询问都没有写什么莫队啊?这不直接双指针?码码码,10 min 搞定。
这个时候大概过了 1h,打算冲 T3。最小值最大考虑二分。T1 T3 全是二分,这是二分专场吗?首先容易想到一个 \(\mathcal O(n^3)\) 左右(std::sort 带 \(\log\))的 check:扫描 \([1,n]\),如果当前位置的高度不够,就选取覆盖当前点的所有区间中右端点前 \(k\) 大的区间然后暴力加就行。差分一下很容易就能做到 \(\mathcal O(n^2)\)。暴力的瓶颈在于相同的区间被多次查询,即使当前区间已经被用过,或者不可能覆盖以后的点。
事实上这个时候已经逼近正解了,但是之前模拟赛做过一道题,是通过链表及时删除不合法决策以避免跑空循环 TLE。这个思路影响了我,所以考场上我写的是链表:把右端点小于当前点和已经被该使用过的区间删去,这样每次只需要遍历整个链表,而非空循环浪费时间。又因为很多点是不用加区间的,完全跑不满。加了几个剪枝,手搓了一个样例,连写带调总共大概花了 1.5h。顺便吐槽题目样例是真的水,我考场上任意时刻的代码都能通过样例。总时间复杂度 \(\mathcal {O}(n^2\log n\log V)\sim \mathcal{O}(n\log n\log V)\)(好像是?)。
T4?你为我会做?打了个爆搜,挂了,懒得鸟他。检查了一下所有文件读写就没了。还有 1h,扫雷启动!同时看到瓜在左边打 T4,隐隐约约在代码里看到一个 Tarjan:果然不是我能碰的题。瓜写完 T4 又回来写 T3,真的是逊,连 T3 都没写/cf
赛后一问,发现 T3 提高二班讲过。czy & cmy & fzy 一起嘲讽我和瓜,伤心,我是不是要垫底了?
预估:\(100 + 100 + [60, 100] + 0 = [260, 300]\)
实际:\(100 + 100 + 100 + 0 = 300\)
一分没挂!T3 暴力甚至在原题拿到了最优解,虽然后来被抢了qwq
提高二班三个 Joker T3 都挂了/cf,写过原题都挂,真的是 Joker。但是 wyz 没挂,太强了!
貌似是 wz 分最高的?瓜挂了 80,惨。cmy T1 文件名打错了,虽然很惨但是真的很好笑(
\(\textbf{7.16}\)
晚上打 Phigros。推了 0.11 的 rks,有点草的说。现在是 rks 15.12。
推完涨 rks 的曲目:三头犬,良怒,DNA,潘多拉,狂喜 AT。
打牌。恭喜千然打破 czy 六把连输的记录,创下了连跪七把的新纪录!
\(\textbf{7.17}\)
题目都没什么意思。AK 了但是数据锅了,伤心。
\(\textbf{7.18}\)
开题的时候真的很激动。结果打的很差,倒一了/kk
\(\textbf{7.19}\)
\(\textbf{T1}\)
模拟赛 A 题放黑你见过吗?
\(\textbf{Description}\)
给定一棵 \(n\) 个节点的树和 \(m\) 条链。
接下来有 \(q\) 次询问,每次询问给出两点,求最少选出几条给定链可以使这两点之间的路径完全被覆盖。
注意题目中的链等价于简单路径。虽然题目指定了有根树,以及同时出现路径和链两种描述有点误导人。
\(1\le n, m, q\le 2\times 10^5\)。
\(\textbf{Sol.}\)
倍增 + 树剖 + 贪心 + 二维数点。
为什么要用树剖?因为我不想用倍增求两点的实际 LCA。不过题目中的类 LCA 依然是用倍增求的。
先考虑一种错解:类似 LCA,一直在所给链上跳,设 \(x\) 和 \(y\) 到 \(\text{LCA}(x,y)\) 分别需要跳 \(t_x,t_y\) 步,那么一起往上跳 \(t_x+t_y\) 步。
显然这个东西随便 Hack。比如说 \(u\) 和 \(v\) 是 \(rt\) 的两个孩子,然后 \(u\) 和 \(v\) 可以被一条链覆盖。
稍微化一下:考虑让 \(x\) 和 \(y\) 调到深度大于 LCA 的深度最小的两个点,记为 \(x^{'}\) 和 \(y^{'}\),设步数分别为 \(t_x^{'}\) 和 \(t_y^{'}\)。那么如果存在一条覆盖 \(x^{'}\) 和 \(y^{'}\) 的链,则答案为 \(t_x^{'}+t_y^{'}+1\),否则为 \(t_x^{'}+t_y^{'}+2\)。如果 \(x\) 或 \(y\) 跳不到这样的情况,那就是 \(-1\)。
那么只需解决如何判断点 \(x\) 和 \(y\) 在一条路劲上。如果这样的路径存在,则这条路径必然从 \(\text{Subtree}(x)\) 走向 \(\text{Subtree}(y)\)。根据 dfs 的一个性质:子树内 \(\text{dfn}\) 连续,所以点 \(x\) 的子树内所有点的 \(\text{dfn}\) 都在 \([\text{dfn}(x),\text{dfn}(x)+\text{siz}(x)-1]\) 内。为了方便,我们将他记为 \([st_x,ed_x]\),同理还有 \([st_y,ed_y]\)。设覆盖 \(x,y\) 的路径为 \(u\rightsquigarrow v\)。那么一定有:
不放把链看做平面直角坐标系的点 \((\text{dfn}(u),\text{dfn}(v))\),那么这就转化为了一个二维数点问题。容斥一下 BIT 即可。
把上面的所有东西结合起来,码量 3.5K 左右,码量不大也不难调。但是我把 \(x\) 和 \(y\) 当成 \(x^{'}\) 和 \(y^{'}\) 用了,调了一个下午心态都炸了/wx,最后还是瓜帮助我调出来的/qq
以下代码是能通过原题 CF983E NN country 的代码。
upd:
xyd 的数据到底在干什么????数据水的话,要么弱的要死暴力随便冲要么单测答案二分测试点 AC,数据 sb 的话,CF AC 的代码交上去还他妈能被卡,你到底在卡什么????我 CF 100 组数据都过了你到底在卡什么???不会出题可以搬,不会改题别瞎几把改好不好???题面 LaTeX 不加时空不给,数据时弱时强时 sb,模拟赛随便找原题应付,我花 2.5w 是来忍你的??????
$\textbf{AC Code}$
#include <bits/stdc++.h>
typedef long long i64;
constexpr int inf = 1 << 30;
constexpr int N = 2e5 + 5;
constexpr int LG = 20;
int n, m, q;
struct Edge { int to, nxt; } E[N];
struct Point { int x, y; } P[N];
struct Que { int x, y, val, id; } Q[N << 2];
int cnt[N], ans[N], tot2;
int head[N], tot;
inline void addEdge(int u, int v) {
E[++tot] = Edge{v, head[u]}, head[u] = tot;
}
int bit[N];
inline void add(int x, int k) {
for(; x <= n; x += (x & -x)) bit[x] += k;
}
inline int qry(int x) {
int res = 0;
for(; x; x -= (x & -x)) res += bit[x];
return res;
}
int fa[N], dep[N], siz[N], son[N];
int dfn[N], top[N], timer;
inline void dfs1(int u, int par) {
dep[u] = dep[par] + 1, fa[u] = par;
son[u] = -1, siz[u] = 1;
dfn[u] = ++timer;
for(int i = head[u], v; i; i = E[i].nxt) {
v = E[i].to; if(v == par) continue;
dfs1(v, u); siz[u] += siz[v];
if(son[u] == -1 || siz[v] > siz[son[u]]) son[u] = v;
}
}
inline void dfs2(int u, int tp) {
top[u] = tp;
if(son[u] == -1) return ;
dfs2(son[u], tp);
for(int i = head[u], v; i; i = E[i].nxt) {
v = E[i].to; if(v ^ son[u]) {
dfs2(v, v);
}
}
}
inline int LCA(int u, int v) {
while(top[u] ^ top[v]) {
if(dep[top[u]] > dep[top[v]]) {
u = fa[top[u]];
} else v = fa[top[v]];
}
return dep[u] < dep[v] ? u : v;
}
int f[N][LG];
inline void dfs3(int u) {
for(int i = head[u]; i; i = E[i].nxt) {
int v = E[i].to; dfs3(v);
if(dep[f[v][0]] < dep[f[u][0]]) {
f[u][0] = f[v][0];
}
}
}
inline std::pair<int, int> cal(int u, int v) {
if(u == v) return std::make_pair(u, 0);
int res = 0;
for(int i = LG - 1; i >= 0; i--) {
if(dep[f[u][i]] > dep[v]) {
u = f[u][i];
res += (1 << i);
}
}
if(dep[f[u][0]] <= dep[v]) return std::make_pair(u, res);
return std::make_pair(u, -1);
}
signed main() {
std::cin.tie(nullptr) -> sync_with_stdio(false);
// std::cin >> n >> m >> q;
std::cin >> n;
for(int u, v = 2; v <= n; v++) std::cin >> u, addEdge(u, v);
dfs1(1, 0), dfs2(1, 1);
dep[0] = inf;
std::cin >> m;
for(int i = 1; i <= m; i++) {
int u, v, lca; std::cin >> u >> v;
if(dfn[u] > dfn[v]) std::swap(u, v);
lca = LCA(u, v), P[i] = Point{dfn[u], dfn[v]};
(dep[lca] < dep[f[u][0]]) && (f[u][0] = lca, 1);
(dep[lca] < dep[f[v][0]]) && (f[v][0] = lca, 1);
}
dfs3(1);
for(int j = 1; j < LG; j++) {
for(int i = 1; i <= n; i++) {
f[i][j] = f[f[i][j - 1]][j - 1];
}
}
std::cin >> q;
for(int i = 1; i <= q; i++) {
int u, v, x, y, lca, tx, ty; std::cin >> u >> v;
lca = LCA(u, v); std::pair<int, int> x_, y_;
x_ = cal(u, lca), y_ = cal(v, lca);
x = x_.first, tx = x_.second;
y = y_.first, ty = y_.second;
if(tx == -1 || ty == -1) { ans[i] = -1; continue; }
if(x == lca) { ans[i] = ty + 1; continue; }
if(y == lca) { ans[i] = tx + 1; continue; }
ans[i] = tx + ty + 2;
if(dfn[x] > dfn[y]) std::swap(x, y);
Q[++tot2] = Que{dfn[x] + siz[x] - 1, dfn[y] - 1, -1, i};
Q[++tot2] = Que{dfn[x] + siz[x] - 1, dfn[y] + siz[y] - 1, 1, i};
Q[++tot2] = Que{dfn[x] - 1, dfn[y] + siz[y] - 1, -1, i};
Q[++tot2] = Que{dfn[x] - 1, dfn[y] - 1, 1, i};
}
std::sort(P + 1, P + m + 1, [](const Point& lhs, const Point& rhs) { return lhs.x < rhs.x; });
std::sort(Q + 1, Q + tot2 + 1, [](const Que& lhs, const Que& rhs) { return lhs.x < rhs.x; });
for(int i = 1, cur = 1; i <= tot2; i++) {
while(cur <= m && P[cur].x <= Q[i].x) add(P[cur].y, 1), cur++;
cnt[Q[i].id] += Q[i].val * qry(Q[i].y);
}
for(int i = 1; i <= q; i++) std::cout << (ans[i] - (cnt[i] > 0)) << '\n';
return 0;
}
宿舍里来了个新同学,xyd 这样真的不好。当天晚上二班一个老师才通知我们,而且我妈问三班班主任他说没有这个安排。
不过新同学看上去人还挺好的也就算了。(upd:第二天就走了)
然后就是喜闻乐见的打牌和打音游。
hsgl 也来打扑克了。这个洗牌和发牌真的是牌佬既视感(
zr 又来了!一个很奇怪的事是每次 zr 说“你们再叫声爹我就走了”的时候,那把牌 zr 必赢。我愿称之为 zrの诅咒。
\(\textbf{7.20}\)
见证 wz 的霸榜!360 rk1 * 3!
\(\textbf{T3}\)
原题 NOI2016 区间。场切了,耶!
\(\textbf{Description}\)
给定 \(n\) 个闭区间。从中选出 \(m\) 个区间,使得这 \(m\) 个区间交集非空。
对于一个合法的选取方案,它的花费为选出的区间长度的极差。即:
最小化该花费。无解输出 \(-1\)。
\(1\le n\le 5\times10^5,1\le m\le2\times 10^5,0\le l,r\le 10^9\)。
\(\textbf{Sol.}\)
这种类似区间覆盖的东西一般都要先排个序。题目要求的和区间长度有关,所以我们先把所有区间按照长度排个序。
于是显然地,最终选出的区间一定在排序后的序列中一定是连续的。于是可以想到双指针。
每次指针移动导致的修改不过是区间覆盖,这个很简单,直接线段树就行。
区间有点大,稍微注意一下离散化,代码也很好写,写得很爽!
$\textbf{AC Code}$
#include <bits/stdc++.h>
typedef long long i64;
constexpr int N = 5e5 + 5;
constexpr int inf = 1 << 30;
int n, m, ans = inf, cnt;
struct Range { int l, r, len; } a[N];
std::vector<int> vec;
inline int find(int x) {
return std::lower_bound(vec.begin(), vec.end(), x) - vec.begin() + 1;
}
struct Node {
int l, r;
int val, tag;
} tr[N << 2];
#define l(u) tr[u].l
#define r(u) tr[u].r
#define lc(u) (u << 1)
#define rc(u) (u << 1 | 1)
#define val(u) tr[u].val
#define tag(u) tr[u].tag
inline void pushup(int u) {
val(u) = std::max(val(lc(u)), val(rc(u)));
}
inline void build(int u, int l, int r) {
l(u) = l, r(u) = r;
if(l == r) return ;
int mid = l + r >> 1;
build(lc(u), l, mid);
build(rc(u), mid + 1, r);
}
inline void pushdown(int u) {
if(!tag(u)) return ;
tag(lc(u)) += tag(u);
tag(rc(u)) += tag(u);
val(lc(u)) += tag(u);
val(rc(u)) += tag(u);
tag(u) = 0;
}
inline void modify(int u, int ql, int qr, int x) {
int l = l(u), r = r(u);
if(ql <= l && r <= qr) {
tag(u) += x;
val(u) += x;
return ;
}
pushdown(u);
int mid = l + r >> 1;
if(ql <= mid) modify(lc(u), ql, qr, x);
if(qr > mid) modify(rc(u), ql, qr, x);
pushup(u);
}
inline int qry() { return val(1); }
signed main() {
std::cin.tie(nullptr) -> sync_with_stdio(false);
std::cin >> n >> m;
for(int i = 1; i <= n; i++) {
std::cin >> a[i].l >> a[i].r;
a[i].len = a[i].r - a[i].l;
vec.push_back(a[i].l), vec.push_back(a[i].r);
}
std::sort(a + 1, a + n + 1, [](Range lhs, Range rhs) { return lhs.len < rhs.len; });
std::sort(vec.begin(), vec.end());
vec.erase(std::unique(vec.begin(), vec.end()), vec.end());
cnt = vec.size() + 2;
build(1, 1, cnt);
for(int i = 1; i <= n; i++) {
a[i].l = find(a[i].l);
a[i].r = find(a[i].r);
}
for(int L = 1, R = 0; L <= n; L++) {
while(R + 1 <= n && qry() < m) {
if(++R == n) return std::cout << (ans == inf ? -1 : ans), 0;
modify(1, a[R].l, a[R].r, 1);
}
ans = std::min(ans, a[R].len - a[L].len);
modify(1, a[L].l, a[L].r, -1);
}
return 0;
}
晚上看推子。看了四集,好看!露比好可爱,我好喜欢!
upd - 7.21:不是怎么没戏份了???
upd - 7.22:好像又有了。诶不是第一季怎么就没了??
\(\textbf{7.21}\)
除了 dp 全切了,rk1 拿下。
\(\textbf{T3}\)
\(\textbf{Description}\)
给定一棵 \(n\) 个节点的树,每个点有一个权值,表示该地商品的物价,记为 \(w_{1\sim n}\)。
现在给出 \(m\) 组询问,每次询问给出 \(s,t\),表示一条路径 \(s\rightsquigarrow t\)。有一个人走过这条路径,依次经过节点 \(s,\dots,u,\dots,v,\dots, t\),他在 \(u\) 点 \(w_u\) 的价钱购买该商品,随后以 \(w_v\) 的价钱在 \(v\) 地区将其出售,请最大化其利润并输出。
\(1\le n,m\le2.5\times 10^5\)。
语文不好题目描述尽量很简洁了qwq
\(\textbf{Sol.}\)
倍增?狗都不写!遇到可爱树上题题,首先考虑树剖 + 线段树!
观察我们需要求的是极差,将树拍到序列上对应的就是带限制的区间极差。令 \(\text{LR}\) 表示左减右的最大值,\(\textbf{RL}\) 表示右减左的最大值。对于一个区间,我们除了维护区间极值以外,还要维护其对应的 \(\text{LR}\) 和 \(\text{RL}\)。
诶这个是不是写的有点抽象啊,那我用数学语言写一下 \(\text{LR}\) 的定义好了(区间为 \([l,r]\)):
然后我们考虑怎么合并两个区间 \([l_1,r_1]\) 和 \([l_2,r_2]\)(以 \(\text{LR}\) 为例)。
对于他们合并之后的区间 \([l^{'},r^{'}]\),记 \(\text{LR}_{[l^{'},r^{'}]}=w_x-w_y(l^{'}\le x<y\le r^{'})\)。
我们对 \(x\) 和 \(y\) 进行分类讨论:
-
\(x,y\in[l_1,r_1]\),此时 \(\text{LR}_{[l^{'},r^{'}]}=\text{LR}_{[l_1,r_1]}\).
-
\(x,y\in[l_2,r_2]\),此时 \(\text{LR}_{[l^{'},r^{'}]}=\text{LR}_{[l_2,r_2]}\).
-
\(x\in[l_1,r_1],\,y\in[l_2,r_2]\),此时 \(\text{LR}_{[l^{'},r^{'}]}=\max_{[l_1,r_1]}-\min_{[l_2,r_2]}\).
那么线段树的 pushup 和 pushdown 就很好写了!
然后回归到树上。如何把两条链拼接起来?首先注意到这个区间合并和区间没有任何关系。如果放在树上,那么下标将失去它的意义,不如直接把它当成一个四元组 \((\max, \min, \text{LR}, \text{RL})\)。
两个四元组可以合并当且仅当他们所代表的路径在树上首尾相接——路径是有向的,它只能是由一个靠近终点的点和一个靠近起点的点点权作差得到的。
当你把路径拆成两条链的时候,对于每条链,它都是以自上而下的方向维护这个四元组的。再详细一点,我们写树剖的时候,代码会有和如下代码相似的片段:
res += query(1, dfn[top[u]], dfn[u]);
所以每次 query 求出的都是 \(\text{top}_u\rightsquigarrow u\) 的最大利润,自上而下。
比如说合并起点 \(s\) 到 LCA 这条链上的信息,对于当前点 \(u\),你应当以 \(\text{top}_u\rightsquigarrow u\) 为“左区间”,以 \(u\rightsquigarrow s\) 为“右区间”,然后再合并。这样,就不抽象了吧?
然后你会得到两条链:一条是 \(\text{LCA}\rightsquigarrow s\),一条是 \(\text{LCA}\rightsquigarrow t\),需要得到的是 \(s\rightsquigarrow t\),因为它不是首尾相接的,所以你不能直接合并它。注意到 \(\text{LR}_{u\rightsquigarrow v}=\text{RL}_{v\rightsquigarrow u}\),那么只需交换左链的 \(\text{LR}\) 和 \(\text{RL}\) 然后再合并即可。
时间复杂度是 \(\mathcal O(m\log^2n)\)。
哦对了这题其实可以带修,如果用我的做法的话。
这里给出带修版原题 [TJOI2015] 旅游 的代码。
这题我调了 2h,为什么呢?因为我宏定义写错了。。
$\textbf{AC Code}$
#include <bits/stdc++.h>
#define int long long
// FastIO
typedef long long i64;
constexpr int N = 1e5 + 7;
constexpr i64 inf = 1ll << 60;
int n, m, a[N];
struct Edge { int to, nxt; } E[N << 1];
int head[N], tot;
inline void addEdge(int u, int v) {
E[++tot] = Edge{v, head[u]}, head[u] = tot;
}
int dep[N], siz[N], fa[N], son[N];
int dfn[N], top[N], rnk[N], timer;
inline void dfs1(int u, int f) {
dep[u] = dep[f] + 1, fa[u] = f;
son[u] = -1, siz[u] = 1;
for(int i = head[u], v; i; i = E[i].nxt) {
v = E[i].to; if(v == f) continue;
dfs1(v, u); siz[u] += siz[v];
if(son[u] == -1 || siz[v] > siz[son[u]]) son[u] = v;
}
}
inline void dfs2(int u, int tp) {
top[u] = tp, dfn[u] = ++timer, rnk[timer] = u;
if(son[u] == -1) return ;
dfs2(son[u], tp);
for(int i = head[u], v; i; i = E[i].nxt) {
v = E[i].to; if(v != son[u] && v != fa[u]) {
dfs2(v, v);
}
}
}
struct Node{
int l, r, Max, Min, LR, RL, tag;
Node() { Max = -inf, Min = inf, tag = LR = RL = 0; }
} tr[N << 2];
#define lc(u) (u << 1)
#define rc(u) (u << 1 | 1)
#define l(u) tr[u].l
#define r(u) tr[u].r
#define tag(u) tr[u].tag
#define Max(u) tr[u].Max
#define Min(u) tr[u].Min
#define LR(u) tr[u].LR
#define RL(u) tr[u].RL
inline Node merge(Node l, Node r){
Node res;
res.Max = std::max(l.Max, r.Max);
res.Min = std::min(l.Min, r.Min);
res.LR = std::max({l.Max - r.Min, l.LR, r.LR});
res.RL = std::max({r.Max - l.Min, l.RL, r.RL});
return res;
}
inline void pushup(int u) {
Max(u) = std::max(Max(lc(u)), Max(rc(u)));
Min(u) = std::min(Min(lc(u)), Min(rc(u)));
LR(u) = std::max({Max(lc(u)) - Min(rc(u)), LR(lc(u)), LR(rc(u))});
RL(u) = std::max({Max(rc(u)) - Min(lc(u)), RL(lc(u)), RL(rc(u))});
}
inline void pushdown(int u) {
if(!tag(u)) return ;
Max(lc(u)) += tag(u), Min(lc(u)) += tag(u);
Max(rc(u)) += tag(u), Min(rc(u)) += tag(u);
tag(lc(u)) += tag(u), tag(rc(u)) += tag(u);
tag(u) = 0;
}
inline void build(int u, int l, int r) {
l(u) = l, r(u) = r;
if(l == r) {
Max(u) = Min(u) = a[rnk[l]];
return ;
}
int mid = l + r >> 1;
build(lc(u), l, mid);
build(rc(u), mid + 1, r);
pushup(u);
}
inline void modify(int u, int ql, int qr, int x) {
int l = l(u), r = r(u);
if(ql <= l && r <= qr) {
Min(u) += x;
Max(u) += x;
tag(u) += x;
return ;
}
pushdown(u);
int mid = l + r >> 1;
if(ql <= mid) modify(lc(u), ql, qr, x);
if(qr > mid) modify(rc(u), ql, qr, x);
pushup(u);
}
inline Node query(int u, int ql, int qr) {
int l = l(u), r = r(u);
if(ql <= l && r <= qr) return tr[u];
int mid = l + r >> 1; Node res;
pushdown(u);
if(ql <= mid) res = query(lc(u), ql, qr);
if(qr > mid) res = merge(res, query(rc(u), ql, qr));
return res;
}
inline void mdf(int u, int v, int w) {
while(top[u] != top[v]) {
if(dep[top[u]] > dep[top[v]]) {
modify(1, dfn[top[u]], dfn[u], w);
u = fa[top[u]];
} else {
modify(1, dfn[top[v]], dfn[v], w);
v = fa[top[v]];
}
}
if(dep[u] > dep[v]) modify(1, dfn[v], dfn[u], w);
else modify(1, dfn[u], dfn[v], w);
}
inline int qry(int u,int v) {
Node l, r; l.Min = r.Min = inf;
while(top[u] != top[v]) {
if(dep[top[u]] > dep[top[v]]) {
l = merge(query(1, dfn[top[u]], dfn[u]), l);
u = fa[top[u]];
} else {
r = merge(query(1, dfn[top[v]], dfn[v]), r);
v = fa[top[v]];
}
}
if(dep[u] > dep[v]) l = merge(query(1, dfn[v], dfn[u]), l);
else r = merge(query(1, dfn[u], dfn[v]), r);
std::swap(l.LR, l.RL);
return merge(l, r).RL;
}
signed main() {
read(n);
for(int i = 1; i <= n; i++) read(a[i]);
for(int i = 1; i < n; i++) {
int u, v; read(u, v);
addEdge(u, v), addEdge(v, u);
}
dfs1(1, 0), dfs2(1, 1);
build(1, 1, n);
for(read(m); m--; ) {
int x, y, c;
read(x, y, c);
writeln(qry(x, y));
mdf(x, y, c);
}
return flush(), 0;
}
\(\textbf{7.22}\)
补题,补题,补题。补完了,耶!
\(\textbf{Exam #2}\)
考场上写的游寄:
全是原题,虽然有几道 dp 我不会,但是一道今天刚写一道很简单,所以没啥问题。
七点左右码完了。差不多时候瓜说他也写完了,一起去上了个厕所。
懒得上拍,静态顶针代码,感觉没啥问题,就开始玩耍了。
最开始是扫雷和纸牌,但是有一个老师好像不让我玩,不开心/ng
用画图给瓜画了一张画!好玩!

还好我带了 U 盘,现在可以写游记和闲话了,也挺好的。
\(\textbf{7.23}\)
空虚。早上打 MC 和臀,都只打了 1h 左右。中途去听了那个 sb 美术鉴赏,蛮无语的不想说,事后我才知道我可以不用去。
下午则一直在看推子的漫画。晚饭吃了 KFC,很好吃。然后会机房,给这篇博客填坑。
\(\textbf{7.24}\)
AK 了非常开心!瓜也 AK 了,但是 ocean 记搜挂了,不然 wz 就是 400 400 320 直接霸榜了。
\(\textbf{T2}\)
非常好玩的(?)题!我也不知道这是什么类型的题,它像 dp,像数学,像找规律,但感觉都不能说/yun
\(\textbf{Description}\)
题意很简洁!注意一下这个光线可以反射 & 透光很多次!
\(\textbf{Sol.}\)
首先它一看就是一个找规律递推的东西。
观察你要求的是光线从 \(1\) 好玻璃射入一次叠放的前 \(i\) 面玻璃的透光率,所以直接设:
-
\(F_i\) 为光线从 \(1\) 号玻璃射入依次叠放的前 \(i\) 面玻璃后的透光率。
-
\(G_i\) 为光线从 \(i\) 号玻璃射入依次叠放的前 \(i\) 面玻璃后的反射率。
对于 \(F\) 的构造非常显然,但是有必要对 \(G\) 进行一些说明:
第 \(i\) 面玻璃与 \(i-1\) 面玻璃的区别在于:部分光线通过第 \(i\) 面玻璃反射到第 \(i-1\) 面玻璃后进行了复杂的透光 & 反射。直接计算是不可做的(无限反射),所以为了把前 \(i-1\) 面玻璃等价为一面玻璃,我们引入了 \(G\) 以解决从 \(i\) 射入 \(i-1\) 的光线。把 \(G_{i-1}\) 看成 \(b_{i-1}\),每次递推就等价于只有两面玻璃的情况了!
然后看两张图:
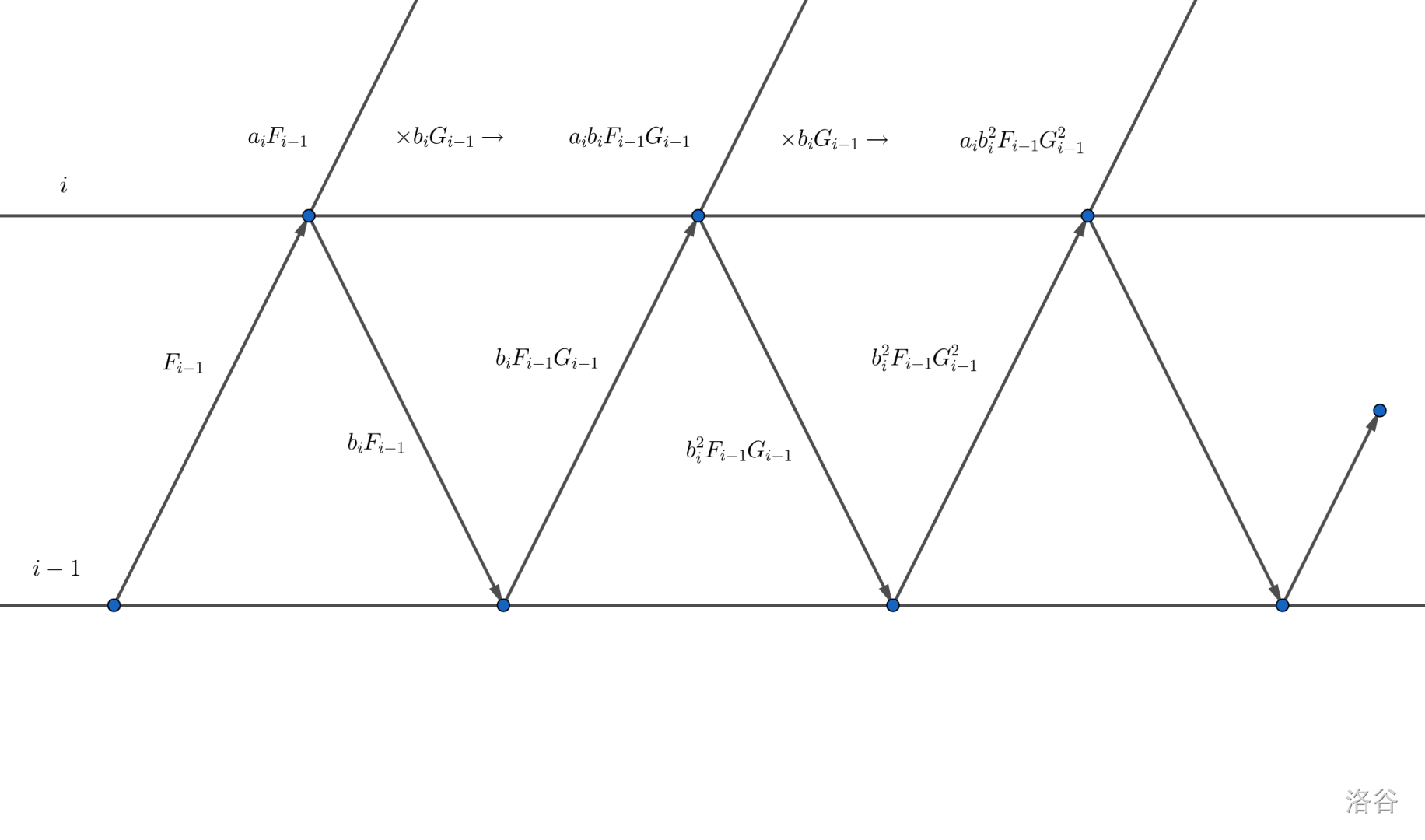
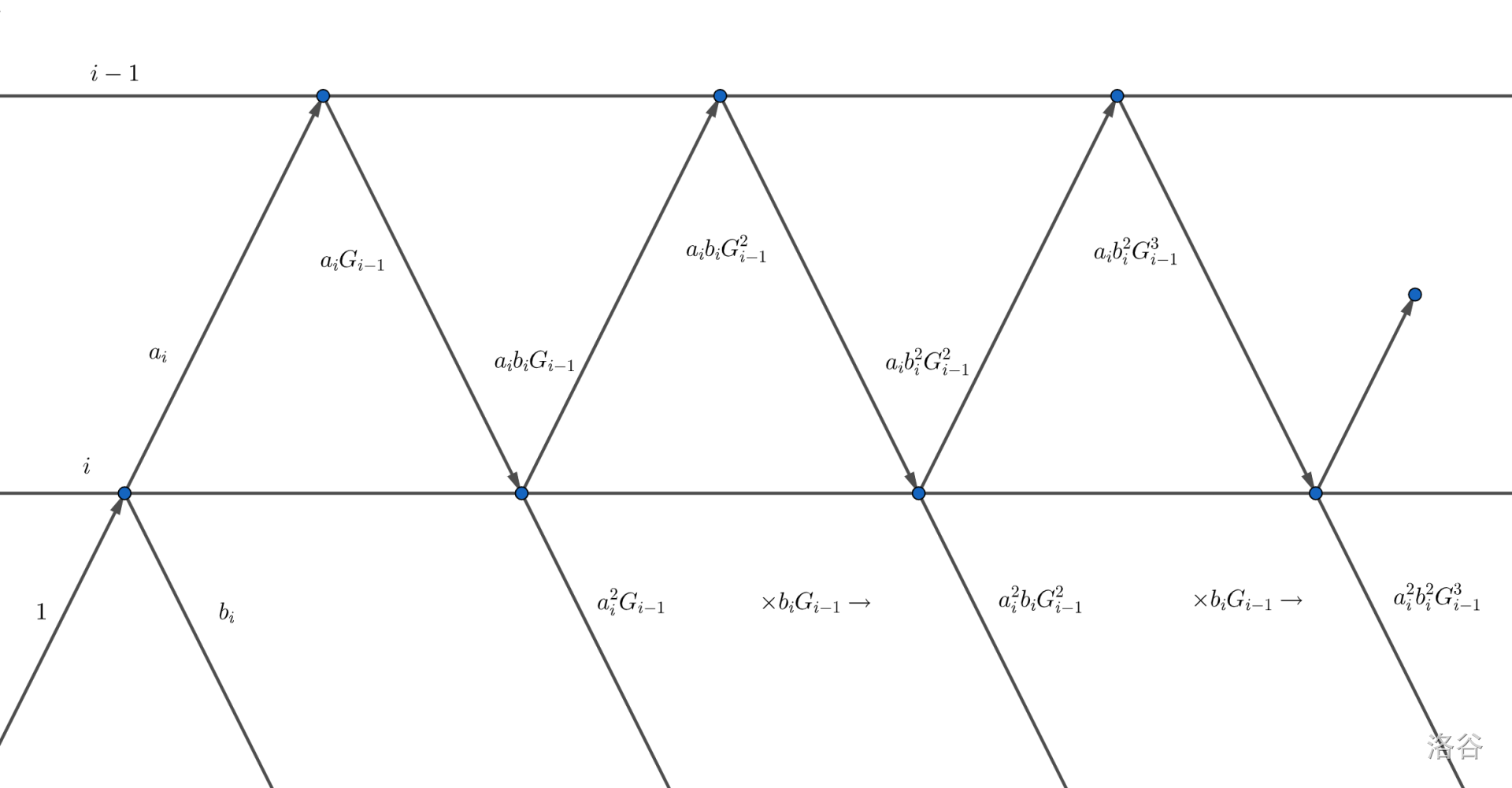
好丑啊,用 \(\sum\) 来写。
对于 \(\sum_{k=0}^{\infty}x^k(|x|<1)\),由等比数列求和公式知:
于是再简化一下这两个递推式:
因为 \((F_i,G_i)\) 可以直接由 \((F_{i-1},G_{i-1})\) 推出,所以空间可以压成 \(\mathcal O(1)\),虽然没用。
时间复杂度 \(\mathcal O(n)\)。
$\textbf{AC Code}$
#include <bits/stdc++.h>
#define int long long
typedef long long i64;
constexpr int N = 3e3 + 5;
constexpr int p = 1e9 + 7;
constexpr int inv100 = 570000004;
int n, a, b, F = 1, G;
inline int qpow(int a, int b) {
int res = 1;
for(; b; b >>= 1) {
if(b & 1) res = res * a % p;
a = a * a % p;
}
return res;
}
inline int inv(int x) {
return qpow(x, p - 2);
}
signed main() {
std::cin.tie(nullptr) -> sync_with_stdio(false);
for(std::cin >> n; n--; ) {
std::cin >> a >> b;
a = a * inv100 % p, b = b * inv100 % p;
int div = inv(1ll - G * b % p + p);
F = (F * a % p * div) % p;
G = (b + a * a % p * G % p * div % p) % p;
}
std::cout << F << '\n';
return 0;
}
\(\textbf{7.25}\)
今天的题目还挺好玩的,但是我不想写题解qwq
T1 是 sb 并查集 / 二分图 染色。我没写!!??
T2 是 [NOIP2017 提高组] 列队,我写了 pbds 并且 AC 了,但是我看到时限很紧删去了一条重要的语句并且后面没加(
世界名画:
//#define int long long
T3 是 [TJOI2015] 概率论,没啥好说的。
T4 正确复杂度非正解过了!
\(\textbf{T4}\)
\(\textbf{Description}\)
题面很简洁!懒得概括了: [POI2011] MET-Meteors
\(\textbf{Sol.}\)
首先这个环对解题没有任何影响,直接破环成链就行。
对操作进行分块。每 \(B\) 个操作为一组,对于每组操作,用差分实现区间加,然后扫描所有国家,如果这个国家已经收集够了,那自然可以跳过;如果经过这组操作,该国家的需求可以被满足,则使该国家达到需求的操作必然属于这一组。倒序扫描块即可。
由于每个国家只会被计算一次,对所有「倒序扫描」求 \(\sum\) 得上界 \(mB\),一共要做 \((k/B)\) 次差分,所以时间复杂度是:
所以块长应当取 \(B = \sqrt k\)。代码中 \(k\) 用 \(Q\) 表示。
$\textbf{AC Code}$
#include <bits/stdc++.h>
typedef long long i64;
constexpr int N = 3e5 + 5;
int n, m, Q, len, p[N], bel[N], ans[N];
i64 a[N], d[N], sum[N];
std::vector<int> vec[N];
struct que { int l, r; i64 k; } q[N];
inline void add(int l, int r, i64 x) {
d[l] += x, d[r + 1] -= x;
}
signed main() {
std::cin.tie(nullptr) -> sync_with_stdio(false);
std::cin >> n >> m;
for(int i = 1; i <= m; i++) {
int o; std::cin >> o;
vec[o].push_back(i);
bel[i] = o;
}
for(int i = 1; i <= n; i++) std::cin >> p[i];
std::cin >> Q;
len = pow(Q, 0.5);
for(int blk = 1, tot = (Q - 1) / len + 1; blk <= tot; blk++) {
memset(a, 0, sizeof(a));
memset(d, 0, sizeof(d));
int L = (blk - 1) * len + 1, R = std::min(blk * len, Q);
for(int i = L; i <= R; i++) {
i64 l, r, k; std::cin >> l >> r >> k;
if(l <= r) add(l, r, k);
else add(l, m, k), add(1, r, k);
q[i].l = l, q[i].r = r, q[i].k = k;
}
for(int i = 1; i <= m; i++) {
a[i] = a[i - 1] + d[i];
sum[bel[i]] += a[i];
}
for(int o = 1; o <= n; o++) {
i64 cur = sum[o];
if(ans[o] || cur < p[o]) continue;
for(int i = R; i >= L; i--) {
int l = q[i].l, r = q[i].r;
i64 k = q[i].k;
for(auto u : vec[o]) {
if((l <= r && l <= u && u <= r) || (l > r && (l <= u || u <= r))) {
cur -= k;
}
}
if(cur < p[o]) {
ans[o] = i;
break;
}
}
}
}
for(int i = 1; i <= n; i++) {
if(ans[i]) std::cout << ans[i] << '\n';
else std::cout << "NIE\n";
}
return 0;
}
\(\textbf{7.26}\)
只写了两道绿......有一道还挂了...
\(\textbf{T2}\)
\(\textbf{Description}\)
一个人在该图上进行随机游走,初始时他在 \(1\) 号节点,每一步会以等概率随机选择一条相邻的边,沿着这条边走到下一个节点,并获得经过边的权。
在到达 \(n\) 号节点后游走结束,总分为获得的边权和。现在,对着 \(m\) 条边编号,使得他获得的总分期望最小。
\(1\le n \le 250,1\le m\le 125000\)。
原题 [HNOI2013] 游走 中的编号在这里换成了边权,我认为题目描述这样更自然。
\(\textbf{Sol.}\)
边权?那玩意是啥?看到边什么的果断转成点!
设 \(E(u)\) 为点 \(u\) 的经过次数的期望。对于所有 \((u,v)\in E\),结点 \(v\) 都有 \((1/\text{deg}(v))\) 的概率在下一步选择 \(u\)。因此:
需要注意的是,条件 \((u,v)\in E\) 并不完全对。点 \(v\) 对点 \(u\) 有贡献,当且仅当点 \(v\) 在下一步有概率选择 \(u\)。所以会有特殊情况:
对于 \(1\) 号结点,除了其他点转移而来的贡献,初始以 \(1\) 为结点这一条件已经为 \(E(1)\) 带来了 \(1\) 的贡献。
对于 \(n\) 号结点,它不能由任何点转移而来,所以 \(E(n)\equiv 0\)。
于是你得到了一个 \((n-1)\) 元线性方程组(\(E(n)=1\),可以直接忽略),高斯消元可以解得所有点经过次数的期望。
那么点的问题就搞定了,现在来看看怎么重新转化为边。你当然可以 dfs 下传点权,但是我懒得搞。
边连接的是两个点,因此对于 \(e=(u,v)(u\ge n, v\ge n)\),它的期望经过次数 \(E^{'}(e)\) 可以通过 \(E(u)\) 和 \(E(v)\) 表示。
总分的期望就是:
由排序不等式可知,大的点权应当与期望经过次数小的值相乘。直接 std::sort 就完事了。
为什么我要浪费篇幅来讲这个?因为我觉得排序不等式的证明很好玩(调整法),大家有兴趣可以 bdfs。
$\textbf{AC Code}$
#include <bits/stdc++.h>
typedef long long i64;
constexpr int N = 505;
constexpr int M = 125005;
constexpr double eps = 1e-10;
int s[M], t[M], deg[N];
struct Edge { int to, nxt; } E[M << 1];
int head[N], tot;
inline void addEdge(int u, int v) {
E[++tot] = Edge{v, head[u]}, head[u] = tot;
}
long double a[N][N], f[M], ans = 0;
inline void Gauss(int n) {
for(int i = 1; i <= n; i++) {
int pos = i;
for(int j = i + 1; j <= n; j++) {
if(a[j][i] > a[pos][i]) {
pos = j;
}
}
for(int j = 1; j <= n + 1; j++) {
std::swap(a[i][j], a[pos][j]);
}
if(fabs(a[i][i]) < eps) continue;
for(int j = i + 1; j <= n + 1; j++) a[i][j] /= a[i][i];
a[i][i] = 1;
for(int j = 1; j <= n; j++) {
if(i == j) continue;
for(int k = i + 1; k <= n + 1; k++) {
a[j][k] -= a[j][i] * a[i][k];
}
a[j][i] = 0;
}
}
}
int n, m;
signed main() {
std::cin.tie(nullptr) -> sync_with_stdio(false);
std::cin >> n >> m;
for(int i = 1; i <= m; i++) {
std::cin >> s[i] >> t[i];
addEdge(s[i], t[i]), deg[s[i]]++;
addEdge(t[i], s[i]), deg[t[i]]++;
}
for(int u = 1; u < n; u++) {
a[u][u] = 1;
for(int i = head[u], v; i; i = E[i].nxt) {
if((v = E[i].to) ^ n) a[u][v] = -1.0 / deg[v];
}
}
a[1][n] = 1;
Gauss(n - 1);
for(int i = 1; i <= m; i++) {
int u = s[i], v = t[i];
f[i] = a[u][n] / deg[u] + a[v][n] / deg[v];
}
std::sort(f + 1, f + m + 1);
for(int i = 1; i <= m; i++) {
ans += f[i] * (m - i + 1);
}
std::cout << std::fixed << std::setprecision(3);
std::cout << ans << '\n';
return 0;
}
\(\textbf{T3}\)
傻逼缝合怪。没想到图可能不联通,保龄。
\(\textbf{Description}\)
Subtask 123 好无聊好困难!我们只看我推出来了的 Subtask4!
给定一张 \(n\) 个点 \(m\) 条边的无向图。现在用 \(k\) 种颜色对这张图(中的所有点)进行染色,要求有边相邻的点不同色。
求染色方案数。答案对 \(10^9+7\) 取模。多测,\(q\le 1000\)。
Subtask4:保证每个点的度数均为 \(2\)。\(1\le n\le 10^5,0\le m\le \min(10^5,n(n−1)/2), 1\le k\le 10^9\)。
\(\textbf{Sol.}\)
如果尝试固定 \(n\),改变 \(k\),推导好像有些困难,因为你难以寻找递推式:毕竟是 OI,肯定要先考虑递推和 dp 这些方面。
因此我们考虑将 \(k\) 视为常数,并将不同 \(n\) 代入取得的染色方案数看成一个数列 \(\{a_n\}\) 以便递推。
下面给出一种方法:
破环成链。考虑一个 \(1\times n\) 的方格,用 \(k\) 种颜色对这个方格进行染色。设第 \(i\) 个格子的颜色为 \(col_i\)。
第一个方格可以填 \(k\) 种颜色,接下来每个方格都有 \(k-1\) 种选择。显然此时的染色方案数为 \(k(k-1)^{n-1}\)。
环和链的区别在于环把链首尾相接。然而首尾相接可能因为首尾颜色的异同造成结果的差异。所以我们分类讨论:
-
\(col_1\ne col_n\) 时,首尾相接就是环的情况,方案数为 \(a_n\)。
-
\(col_1 = col_n\) 时,首尾相接后会出现长度为 \(2\) 的颜色段,把这个颜色段看成单独的一个点,就等价于大小为 \(n-1\) 的环,故方案数为 \(a_{n-1}\)。
于是 \(a_n+a_{n-1}=k(k-1)^{n-1}\)。剩下就是很简单的数列问题了。
同构:
显然 \(a_n\ge (k-1)^n\),因此数列 \(\{a_n-(k-1)^n\}\) 是首项为 \(1 - k\),公比为 \(-1\) 的等比数列。
故
上面的推导看上去有一个问题,那就是为什么 \(a_1-(k-1)^1=k-1\)。看上去只有一个点的染色方案数应该是 \(k\),所以首项是 \(1\)。
其实这推导并没有问题。我们定义的时候默认背景是环,而一个 \(n\) 元环应该有 \(n\) 条边,故 \(n=1\) 的情况实际上是一个自环,自己和自己相邻,因此不存在合法的染色方案,即 \(a_1=0\)。
同理 \(n=2\) 并不是两点一线,而是一个重边。当然它不影响答案。
$\textbf{AC Code}$
你以为我会给代码?我把它当数学题写的。
我保龄的原因是因为图不一定联通,也就是说可有多个环。
\(\textbf{7.27}\)
T2 很神,我不会做。
\(\textbf{T3}\)
\(\textbf{Description}\)
小 h 正在看书,他从第 \(k\) 页开始看,准备看到第 \(m\) 页。
小 h 可以跳着看书,如果看完第 \(x\) 页,下一次他可以选择 \([x+1,x+d]\) 这个区间内任意一页看,且每跳一次小 h 会花费 \(a\) 的代价。
这本书中有 \(n\) 页在看完之后能获得一定的收益。看完 \(x_i\) 页可以获得 \(v_i\) 的收益。
求从第 \(k\) 页跳着看到第 \(m\) 页的最大收益。
\(\textbf{Sol.}\)
设
$\textbf{AC Code}$
#include <bits/stdc++.h>
#define int long long
typedef long long i64;
constexpr int N = 1e5 + 5;
constexpr int M = 2e6 + 5;
constexpr int inf = 1e18;
int n, m, k, d, a;
int x[N], v[N], c[N], r[N], f[N];
struct Node {
int lc, rc;
int Max = -inf;
} tr[M];
int tot, rt;
#define lc(u) tr[u].lc
#define rc(u) tr[u].rc
#define Max(u) tr[u].Max
#define NewNode() (++tot)
inline void pushup(int u) {
Max(u) = std::max(Max(lc(u)), Max(rc(u)));
}
inline void modify(int &u, int l, int r, int pos, int x) {
if(!u) u = NewNode();
if(l == r) return Max(u) = std::max(Max(u), x), void();
int mid = l + r >> 1;
if(pos <= mid) modify(lc(u), l, mid, pos, x);
else modify(rc(u), mid + 1, r, pos, x);
pushup(u);
}
inline int query(int u, int l, int r, int ql, int qr) {
if(!u) return -inf;
if(ql <= l && r <= qr) return Max(u);
int mid = l + r >> 1, res = -inf;
if(ql <= mid) res = std::max(res, query(lc(u), l, mid, ql, qr));
if(qr > mid) res = std::max(res, query(rc(u), mid + 1, r, ql, qr));
return res;
}
signed main() {
std::cin.tie(nullptr) -> sync_with_stdio(false);
std::cin >> k >> m >> d >> a >> n;
for(int i = 2; i <= n + 1; i++) std::cin >> x[i] >> v[i];
x[1] = k, x[n += 2] = m;
for(int i = 1; i <= n; i++) {
c[i] = x[i] / d;
r[i] = x[i] % d;
}
modify(rt, 0, d - 1, r[1], a * c[1]);
for(int i = 1; i <= n; i++) {
f[i] = std::max(query(rt, 0, d - 1, 0, r[i] - 1) - a, query(rt, 0, d - 1, r[i], d - 1)) + v[i] - a * c[i];
modify(rt, 0, d - 1, r[i], f[i] + a * c[i]);
}
std::cout << f[n] << '\n';
return 0;
}
/*
f[i] = max(f[j] - (xi - xj) / D * A + vi) = vi + A * max[f[j] + (xj - xi) / D]
xi = ci * D + ri
f[i] = vi + A * max[Fj + (D(cj - ci) + (rj - ri)) / D]
= vi + A * max[Fj + (cj - ci) + (rj - ri) / D]
= vi + A * max[Fj + cj + (rj - ri) / D] - A * ci
= (vi - A * ci) + max[Fj + A * cj + A(rj - ri) / D]
I. (rj - ri) / D = -1
II. (rj - ri) / D = 0
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号